Тема 1. Кинематика

1. Траектория, путь, перемещение. Скорость

Материа́льная то́чка (МТ) – простейшая физическая модель в механике – математическая абстракция – тело, размеры которого допустимо считать бесконечно малыми по отношению к остальным объектам исследуемой задачи. Под материальной точкой понимают обладающее массой тело, размерами и формой которого можно пренебречь при решении данной задачи.

МТ при движении описывает некоторую линию, называемую траекторией. В зависимости от формы траектории различают прямолинейное движение, движение по окружности, криволинейное движение и др. Пусть МТ переместилась вдоль некоторой траектории из точки 1 в точку 2 (Рис. 1).

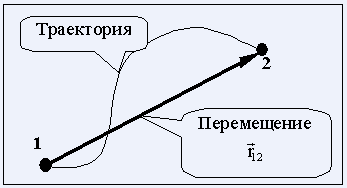
Рис. 1. Траектория и перемещение материальной точки

Расстояние между этими точками, измеренное при движении МТ по траектории, имеет значение пройденного пути s. Направленный отрезок прямой, проведенный из точки 1 в точку 2, называется перемещением. Перемещение – это величина, характеризующаяся численным значением и направлением, имеет геометрический смысл вектора. Действительно, пусть имеем одинаковые по величине перемещения МТ из точки 1 в точку 2 и 3 (Рис. 2, а).

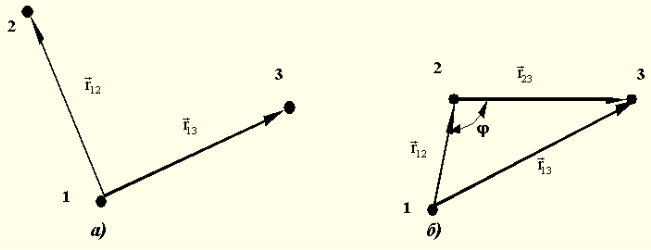
Рис. 2. Векторы перемещения материальной точки: а) неэквивалентность результата перемещения при одинаковой длине вектора; б) сложение векторов.

Очевидно, что, хотя величины перемещений одинаковы, результат далеко не равноценен, поскольку МТ оказывается в разных пространственных положениях. Если МТ совершает сложное движение, которое можно описать, например, двумя последовательными перемещениями и , то суммарное перемещение можно задать одним вектором (Рис. 2, б), который задает такое же перемещение. Результат сложения векторов определяется соотношением: (1).

Квадрат модуля вектора (1) в общем случае можно вычислить, используя теорему косинусов: (2), где φ – угол между векторами и .

К числу векторных величин в механике относят скорость, ускорение, силу и ряд других. Длина отрезка в установленном масштабе имеет смысл модуля вектора, стрелкой показывают направление вектора.

Величины, для определения которых достаточно знать одно число, называются скалярными (скалярами). Скалярами являются путь, время, масса, температура и другие.

Положение МТ в пространстве задают с помощью радиус-вектора , проведенного из начала координат системы отсчета в МТ. При движении МТ вектор может изменяться как по величине, так и по направлению. Рассмотрим вектор в некоторый момент времени t (Рис. 3).

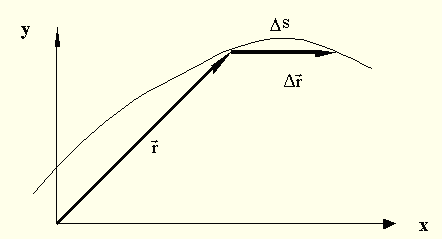
Рис. 3. Радиус-вектор материальной точки в зависимости от времени

За малый (элементарный) промежуток времени Δt МТ проходит элементарный путь Δs, который можно представить с помощью вектора элементарного перемещения . Возьмем отношение: (3), которое также является вектором, совпадающим по направлению с вектором . Ясно, что это отношение зависит от величины промежутка времени Δt. При уменьшении знаменателя дроби (3) будет уменьшаться и числитель. Однако такое уменьшение происходит до определенного предела так, что при достижении весьма малых значений Δt вектор прекращает изменяться как по величине, так и по направлению. Следовательно, отношение (3) стремится к некоторому пределу, который называют скоростью МТ в момент времени t: .(4)

По определению, соотношение (4) представляет собой производную по времени: (5) и называется истинной или мгновенной скоростью МТ. Из Рис. 4 ясно, что вектор является секущей траектории движущейся МТ.

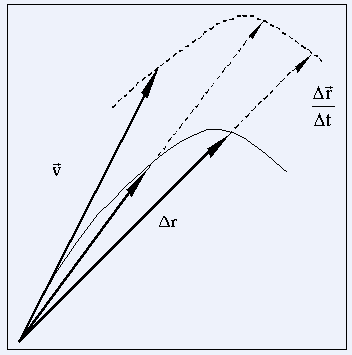
Рис. 4. Скорость как секущая траектории материальной точки

В пределе (4) секущая (скорость МТ) превращается в касательную к траектории.

Элементарный путь Δs в общем случае отличается от модуля элементарного перемещения . Если временной промежуток , то различие между Δs и также становится исчезающе малым. Благодаря этому для модуля скорости можно записать: (6).