
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»
Утверждено
на заседании кафедры физики
20 мая 2011 г.
Методические указания
к лабораторной работе № 9
«ИЗУЧЕНИЕ ОСНОВНОГО ЗАКОНА ДИНАМИКИ
Вращательного движения с помощью прибора
ОБЕРБЕКА»
Ростов-на-Дону
2011
УДК 531.383
Методические указания к лабораторной работе № 9 «Изучение основного закона динамики вращательного движения с помощью прибора Обербека». – Ростов н/Д: Рост. гос. строит. ун-т, 2011. – 10 с.
Методические указания содержат краткую теорию метода, порядок выполнения лабораторной работы, требования техники безопасности, требования к оформлению результатов, а также перечень контрольных вопросов и тестов.
Предназначены для выполнения лабораторной работы по программе курса общей физики для студентов всех специальностей РГСУ.
УДК 531.383
Составители: проф. Н.Н. Харабаев,
проф. А.Н. Павлов
Рецензент доц. Ю.И. Гольцов
Редактор н.Е. Гладких
Темплан 2011 г., поз. ___
Подписано в печать ____). Формат 60х84 1/16. Бумага писчая. Ризограф. Уч.-изд.л 0,5. Тираж 100 экз. Заказ
Редакционно-издательский центр
Ростовского государственного строительного университета.
334022, Ростов-на-Дону, ул. Социалистическая, 162
© Ростовский государственный
строительный университет, 2011
Лабораторная работа № 9
ИЗУЧЕНИЕ ОСНОВНОГО ЗАКОНА
ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
С ПОМОЩЬЮ ПРИБОРА ОБЕРБЕКА
Цель работы: на опыте изучить действие основного закона динамики вращательного движения.
Приборы и принадлежности: прибор Обербека, секундомер, набор грузов, штангенциркуль, метровая линейка.
Краткая теория эксперимента
Основной закон динамики вращательного движения твердого тела:
![]() ,
где
,
где
![]() –
момент количества
движения твердого тела,
–
момент количества
движения твердого тела,
![]() –
момент внешних
сил, действующих на тело.
–
момент внешних
сил, действующих на тело.
Для
однородного тела, вращающегося
относительно оси симметрии этого
тела:
![]() ,
где
,
где
![]() –
момент инерции
твердого тела относительно его оси
вращения,
–
момент инерции
твердого тела относительно его оси
вращения,
![]() -
угловая скорость.
-
угловая скорость.
Вектор направлен по оси вращения в соответствии с правилом правого винта.
В
этом случае
![]() ,
или
,
или
![]() .
.
Отсюда
![]() ,
где
,
где
-
момент внешней силы
![]() относительно данной оси вращения, то
есть проекция вектора момента внешней
силы
на данную ось вращения (направление
вектора
коллинеарно
оси вращения);
относительно данной оси вращения, то
есть проекция вектора момента внешней
силы
на данную ось вращения (направление
вектора
коллинеарно
оси вращения);
![]() -
угловое ускорение (направление вектора
коллинеарно
оси вращения и совпадает с направлением
вектора
).
-
угловое ускорение (направление вектора
коллинеарно
оси вращения и совпадает с направлением
вектора
).
Таким образом, в рассматриваемом случае основной закон динамики вращательного движения твердого тела относительно неподвижной оси:
если на тело, имеющее ось вращения (совпадающую с осью симметрии данного тела), действует сила, то это тело приобретает угловое ускорение, величина которого прямо пропорциональна моменту действующей силы относительно данной оси вращения и обратно пропорциональна моменту инерции этого тела относительно той же оси вращения.
Согласно этому
закону для какого-либо тела с неизменным
моментом инерции относительно выбранной
оси вращения (оси симметрии данного
тела) величина углового ускорения
линейно зависит от величины момента
действующей силы относительно данной
оси вращения, то есть
![]() .
.
Линейная зависимость
углового ускорения
![]() от величины
от величины
![]() может быть проверена экспериментально
с помощью «прибора Обербека».
может быть проверена экспериментально
с помощью «прибора Обербека».
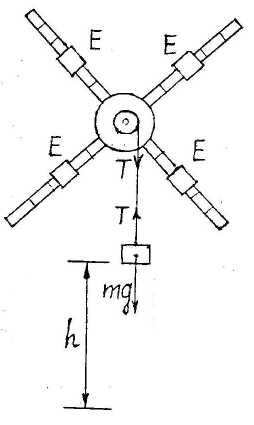
Рис. 1. Принципиальная схема «прибора Обербека»
Прибор Обербека состоит их металлического «креста», способного вращаться вокруг неподвижной оси под действием силы натяжения Т разматывающейся нити, на которой подвешен груз массой m.
Используя набор
грузов с разными массами m1
, m2
, m3
…, с помощью
прибора Обербека можно определить в
результате косвенных измерений моменты
сил натяжения нити:
![]() и
соответствующие им величины углового
ускорения
и
соответствующие им величины углового
ускорения
![]()
По точкам
![]() можно построить экспериментальную
графическую зависимость
можно построить экспериментальную
графическую зависимость
![]() и проверить ее соответствие линейной
зависимости.
и проверить ее соответствие линейной
зависимости.
Момент силы
натяжения нити Т
можно получить из второго закона Ньютона
для поступательного движения груза
m: ![]()
![]() , где
, где
a – ускорение, с которым движется груз,
F
– сила, вызывающая это ускорение:
![]() .
.
Отсюда
![]() ,
а момент этой силы относительно оси
вращения:
,
а момент этой силы относительно оси
вращения:
![]() ,
где
,
где
r – плечо силы Т (r – радиус шкива).
Так как угловое
ускорение
![]() ,
то экспериментальная часть данной
работы состоит в определении радиуса
шкива r
и линейного
ускорения движения груза m.
Радиус шкива r
определяется
с помощью штангенциркуля. Все ускорения
a можно определить опытным путем с
использованием формулы
,
то экспериментальная часть данной
работы состоит в определении радиуса
шкива r
и линейного
ускорения движения груза m.
Радиус шкива r
определяется
с помощью штангенциркуля. Все ускорения
a можно определить опытным путем с
использованием формулы
![]() ,
получаемой из
,
получаемой из
![]() ,
где
,
где
h – путь, пройденный за время t после начала движения груза с ускорением a.
Таким образом, для определения величины ускорения a необходимо провести измерения пути h и времени t движения груза m.
