Расчет пограничного слоя на плоской поверхности в несжимаемой среде

Решение задачи об обтекании плоской пластинки в теории сопротивления играет большую роль. Найденная для пластинки зависимость и величина коэффициента сопротивления трения могут быть использованы при приближенных расчетах других удобообтекаемых тел.

З адача расчета пограничного слоя в несжимаемой среде сводится к определению закона изменения толщины пограничного слоя, т. е. , и силы сопротивления трения при условии, что известны скорость , величина коэффициента кинематической вязкости и хорда пластинки .

Для плоской пластинки (рис. 7.6) скорость потенциального течения , градиент давления вдоль пластинки (пластинка – тело с нулевым градиентом давления вдоль ее хорды). С учетом вышеизложенного интегральное соотношение (7.8) приобретает вид

. (7.10)

Для решения задачи о пограничном слое введем дополнительно еще два соотношения:

1) закон распределения скорости по толщине пограничного слоя ;

2) уравнение, связывающее касательное напряжение на стенке с толщиной пограничного слоя .

Вид этих соотношений зависит от состояния пограничного слоя.

Ламинарный пограничный слой

Рассмотрим закон распределения скорости в виде полинома третьей степени (метод Польгаузена)

. (7.11)

Коэффициенты полинома определим из граничных кинематических и динамических условий:

Кинематические граничные условия:

1) при , ;

2) при , .

Динамические граничные условия:

1) при и из первого уравнения системы (7.6) для пограничного слоя получаем , но и тогда ;

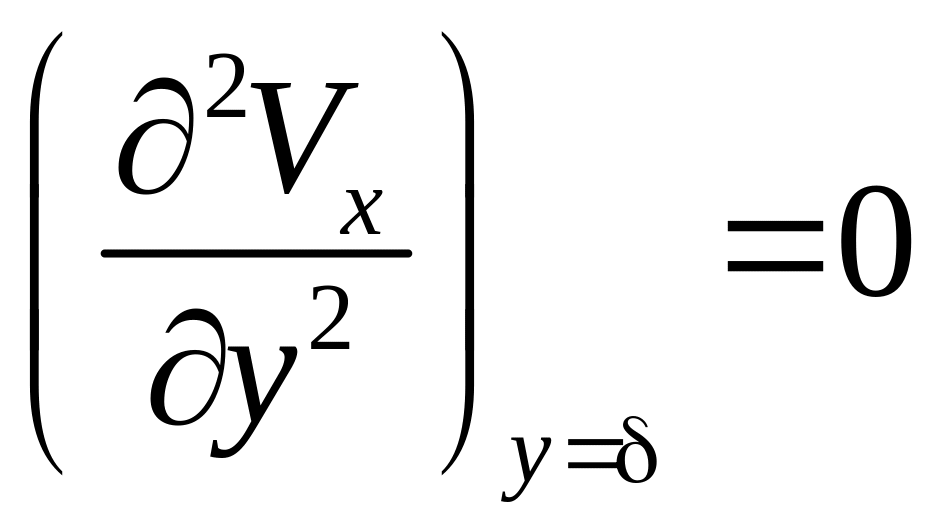2) при сила трения становится равной нулю, т. е. касательные напряжения обращаются в нуль, и отсюда .

Подставляя указанные граничные условия в уравнения (7.11), получим следующую систему уравнений для определения коэффициентов :

, , , .

В результате ее решения определим значения коэффициентов: . Следовательно, закон распределения скорости по сечению ламинарного пограничного слоя принимает вид

. (7.11а)

Выражение для получим из закона Ньютона для внутреннего трения при ламинарном течении: . Из уравнения (7.11а) производная , отсюда:

. (7.12)

Вычислим интегралы, входящие в интегральное соотношение:

и

Подставив эти интегралы в интегральное соотношение (7.10), получим обыкновенное дифференциальное уравнение:

.

Группируя подобные члены и разделяя переменные, получаем . После интегрирования имеем следующее: . Значение произвольной постоянной определим из условий на передней кромке пластинки: при толщина пограничного слоя , следовательно .

В итоге, после небольших преобразований получаем формулу для расчета толщины пограничного слоя:

, или . (7.13)

Как следует из уравнения (7.13), толщина ламинарного пограничного слоя нарастает по параболическому закону. Тогда толщина вытеснения и толщина потери импульса для ламинарного пограничного слоя будут следующие: и .

Введем в рассмотрение местный коэффициент трения , представляющий собой отношение касательных напряжений к скоростному напору:

. (7.14)

Подставив выражение (7.12) в выражение (7.14) с учетом уравнения (7.13), получаем следующее:

или . (7.15)

Формула (7.15) показывает, что местный коэффициент трения, имея максимум вблизи передней кромки, уменьшается при удалении от нее.

Найдем силу трения, действующую на пластинку, учитывая тот факт, что пограничный слой есть на обеих сторонах пластинки (см. рис. 7.6). Запишем выражения для через коэффициент сопротивления трения:

и через касательные напряжения (или местный коэффициент трения):

.

Приравняв правые части этих выражений, получим зависимость для расчета коэффициента сопротивления трения плоской пластинки через местный коэффициент трения:

. (7.16)

С учетом формулы (7.15) формула для коэффициента сопротивления трения плоской пластинки при ламинарном пограничном слое принимает вид

. (7.17)

В уравнении (7.17) в качестве характерного линейного размера в числе Рейнольдса используется хорда пластинки , т. е. .

Турбулентный пограничный слой

Ламинарное течение в пограничном слое плоской пластины возможно лишь в случае, если число Рейнольдса не превышает некоторого значения, называемого критическим. Это значение не является фиксированным, оно зависит от условий входа потока на пластину, состояния ее поверхности и от степени турбулентности набегающего потока. Экспериментальные данные показывают, что критическое число Рейнольдса находится в пределах от до (число Рейнольдса рассчитано по толщине пограничного слоя, т. е. ). Вместо числа Рейнольдса можно рассматривать число Рейнольдса , в котором за характерную длину принято расстояние x от входной кромки пластины. Указанным пределам значений критического числа соответствуют пределы для значений =

П ри числах Рейнольдса, больших критического, ламинарный режим течения в пограничном слое нарушается. Непосредственно за сечением, в котором число Рейнольдса достигает критического значения, находится переходный участок, в котором могут существовать переменные во времени области как ламинарного, так и турбулентного течения, а за этим переходным участком движение в пограничном слое является турбулентным (рис. 7.7). Размеры переходной области зависят от местного градиента давления, чисел М и Re, степени турбулентности и некоторых других факторов. Положение и протяженность переходной зоны могут быть определены экспериментально путем измерения профилей скорости в различных сечениях по длине поверхности.

В непосредственной близости к твердой поверхности поперечные к потоку пульсации скорости весьма малы, и движение здесь всегда ламинарное. Можно условно выделить внутри турбулентного пограничного слоя тонкую прослойку, примыкающую к поверхности пластины, называемую ламинарным подслоем.

Характер изменения профиля скорости при переходе течения в пограничном слое от ламинарного к турбулентному показан на рис. 7.8. Профили скорости в пограничном слое позволяют вычислить толщину потери импульса и по характеру изменения этой величины установить протяженность переходной зоны. С возрастанием числа Рейнольдса точка перехода смещается к передней кромке, длина ламинарного участка у входной кромки убывает и может оказаться весьма малой по сравнению с длиной пластины. Поэтому когда числа Рейнольдса велики, можно в расчетах пренебрегать наличием ламинарного пограничного слоя у входной кромки и рассматривать пограничный слой как турбулентный на всем протяжении.

З аконы турбулентного течения наиболее полно изучены для движения жидкости в круглых трубах. Используем результаты этих исследований для расчета пограничного слоя на плоской пластинке.

Допустим, что в пограничном слое профиль скорости такой же, как и в круглой трубе:

.

Воспользуемся зависимостью касательных напряжений на стенке от и , также полученной для труб: .

Вычислим интегралы, входящие в интегральное соотношение:

, .

После подстановки их, а также выражения для в интегральное соотношение (7.10), в результате простых преобразований получаем

.

Разделяя переменные , после интегрирования и определения произвольной постоянной (как и для ламинарного пограничного слоя, она равна нулю) получим следующее:

или . (7.18)

То есть толщина турбулентного пограничного слоя нарастает более интенсивно, чем у ламинарного пограничного слоя (табл. 7.1). Тогда толщина вытеснения и толщина потери импульса равны:

Таблица 7.1