
- •Глава 5 плоские изоэнтропические течения газа
- •Основное дифференциальное уравнение плоского потенциального потока газа
- •Метод малых возмущений
- •Линеаризованное обтекание тупого угла сверхзвуковым потоком
- •Метод характеристик Метод характеристик позволяет рассчитать сверхзвуковое течение газа с помощью системы характеристик в плоскости потока и годографа скорости. Характеристики в плоскости потока
- •С. . Схема к задаче Коши
- •Обтекание сверхзвуковым потоком выпуклого угла (течение Прандтля–Майера)
- •Контрольные вопросы и задания
Обтекание сверхзвуковым потоком выпуклого угла (течение Прандтля–Майера)
Рассмотрим
равномерный сверхзвуковой поток газа,
движущийся со скоростью
![]() вдоль прямолинейной стенки АО.
В точке О
стенка отклоняется на угол
вдоль прямолинейной стенки АО.
В точке О
стенка отклоняется на угол
![]() от первоначального направления (рис.
5.8). В результате поворота сверхзвукового
потока на угол
скорость
от первоначального направления (рис.
5.8). В результате поворота сверхзвукового
потока на угол
скорость
![]() увеличивается (
).
Проведем из угловой точки О
линию возмущения ОВ,
угол наклона которой определится
через известное соотношение
увеличивается (
).
Проведем из угловой точки О
линию возмущения ОВ,
угол наклона которой определится
через известное соотношение
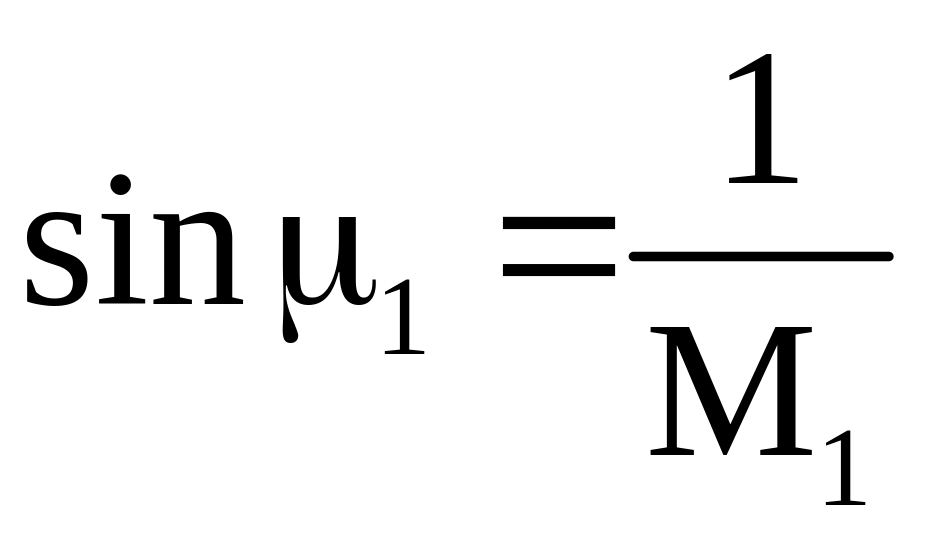 (рис. 5.8, а).
(рис. 5.8, а).
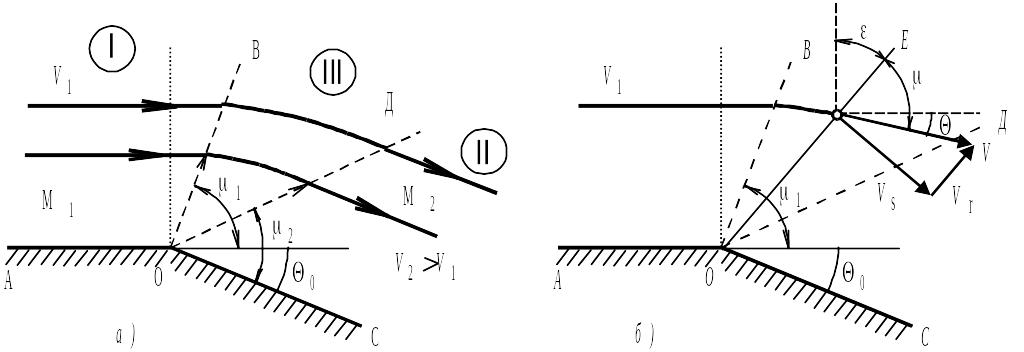
а б
Рис. 5.8. Обтекание выпуклого угла сверхзвуковым потоком:
а – параметры течения в области I, II; б – параметры течения в области III
Линия
ОВ
– граница области возмущенного (III) и
невозмущенного (I) движений. Так как в
области I
= const, то линия ОВ
совпадает с характеристикой, и на
основании задачи Гурса все характеристики
этого семейства, исходящие из точки О,
– прямые линии. Вдоль каждой такой
прямой скорость постоянна по величине
и направлению. Для потока, движущегося
после поворота вдоль стенки ОС
со
скоростью
,
проведем линию возмущения (характеристику
ОD)
под углом
![]() к ОС,
где
к ОС,
где
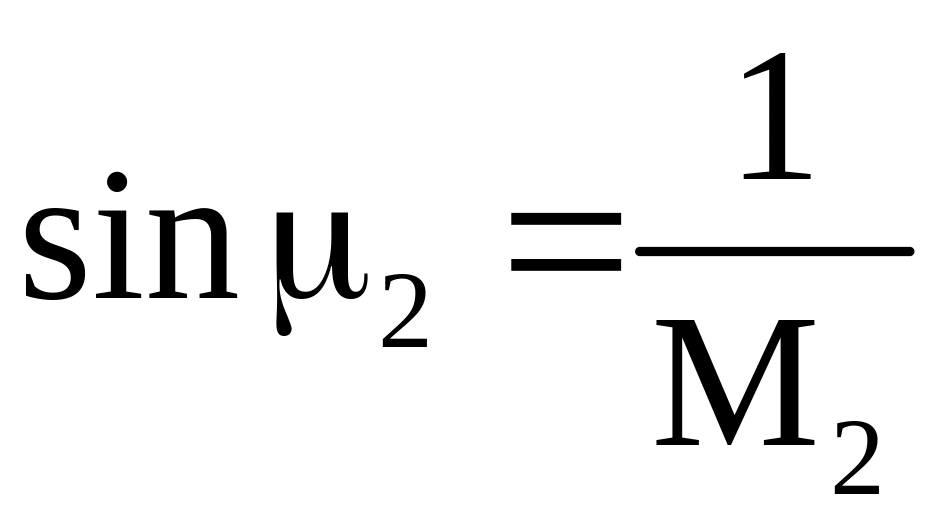 .
Линия ОD
является нижней границей области
возмущений III (ВОD),
где происходит непрерывное изменение
величины и направления вектора скорости
от
до
.
.
Линия ОD
является нижней границей области
возмущений III (ВОD),
где происходит непрерывное изменение
величины и направления вектора скорости
от
до
.
Найдем параметры течения в области возмущенного движения III (рис. 5.8, б).
Введем
полярные координаты r
и
![]() .
За положительное направление отсчета
угла
будем считать направление по часовой
стрелке. Разложим вектор скорости
на направления: r
– вдоль радиуса (составляющая скорости
.
За положительное направление отсчета
угла
будем считать направление по часовой
стрелке. Разложим вектор скорости
на направления: r
– вдоль радиуса (составляющая скорости
![]() )
и s
– перпендикулярно радиусу (составляющая
)
и s
– перпендикулярно радиусу (составляющая
![]() ).
Вдоль характеристики, т. е. в направлении
радиуса-вектора r,
параметры течения газа неизменны,
поэтому составляющие скорости
и
зависят только от угла
.
).
Вдоль характеристики, т. е. в направлении
радиуса-вектора r,
параметры течения газа неизменны,
поэтому составляющие скорости
и
зависят только от угла
.
Считая
движение газа потенциальным, введем
потенциал скорости
![]() и запишем выражения для составляющих
скорости:
и запишем выражения для составляющих
скорости:
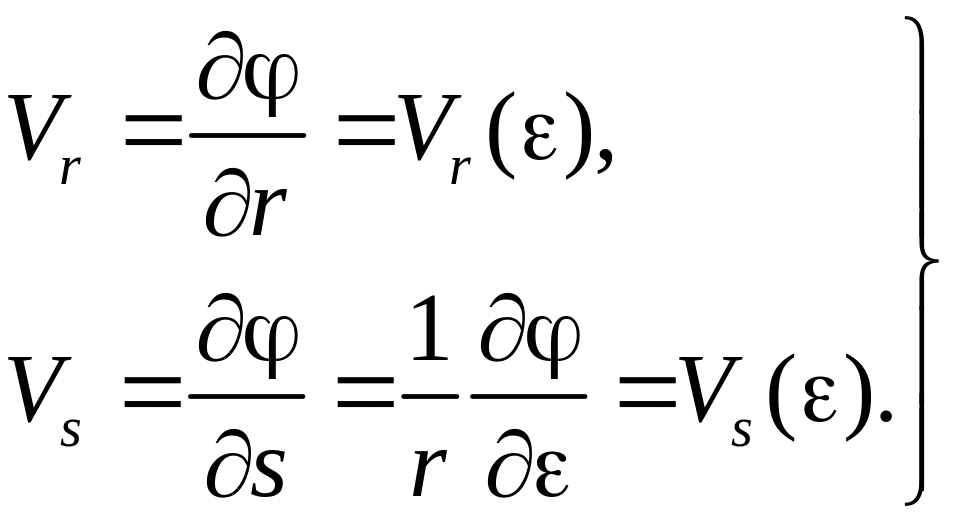 (5.23)
(5.23)
В качестве исходного уравнения для решения поставленной задачи запишем уравнение энергии (уравнение Бернулли) в виде
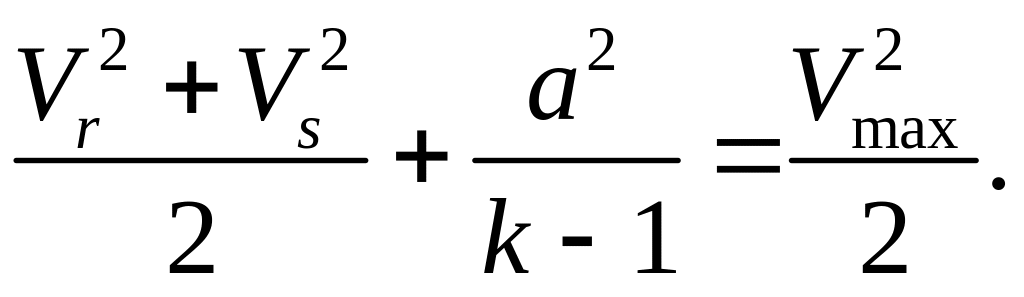 (5.24)
(5.24)
Как
известно, составляющая вектора скорости
в направлении, перпендикулярном к линии
возмущения, всегда равна скорости звука
,
т. е.
![]() .
.
Рассмотрим
производную
 ,
которая с учетом выражений (5.23) запишется
в виде
,
которая с учетом выражений (5.23) запишется
в виде
![]() .
Так как
и
не зависят от радиуса (равномерное поле
скоростей), то
.
Так как
и
не зависят от радиуса (равномерное поле
скоростей), то
![]() .
Следовательно,
.
Следовательно,
![]() и
и
![]() .
.
Поэтому уравнение энергии (5.24) перепишется следующим образом:
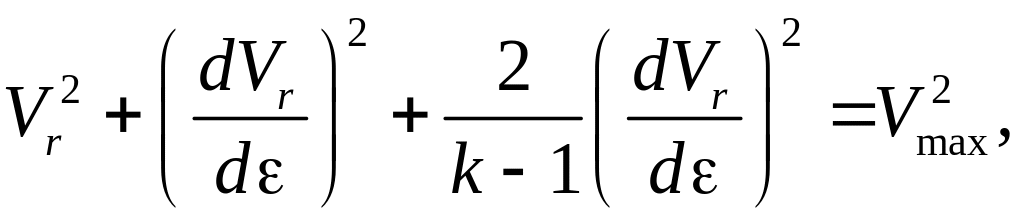
или
после преобразований:
 .
Находя корни этого квадратного уравнения,
будем иметь в виду, что в направлении
течения скорость движения газа возрастает,
т. е.
.
Находя корни этого квадратного уравнения,
будем иметь в виду, что в направлении
течения скорость движения газа возрастает,
т. е.
![]() .
Поэтому получаем, что
.
Поэтому получаем, что
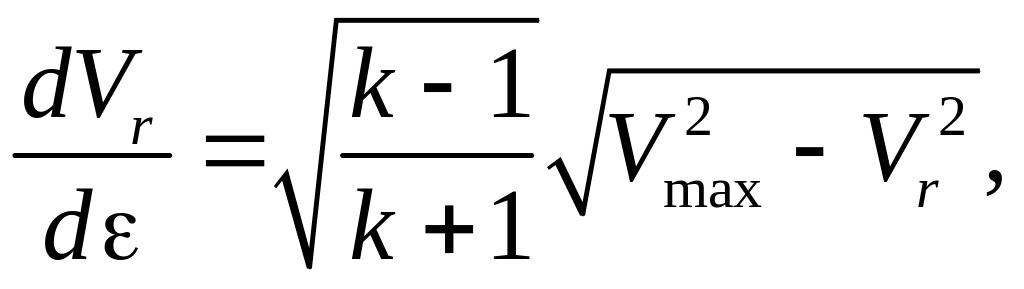 и после разделения переменных и
интегрирования имеем следующее:
и после разделения переменных и
интегрирования имеем следующее:
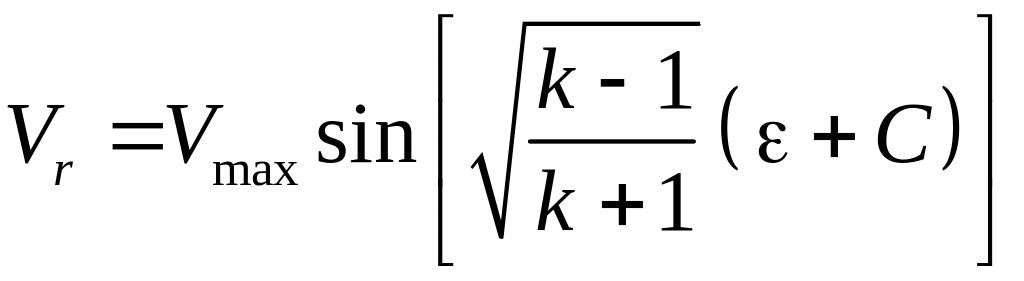 .
(5.25)
.
(5.25)
Так
как
![]() ,
то
,
то
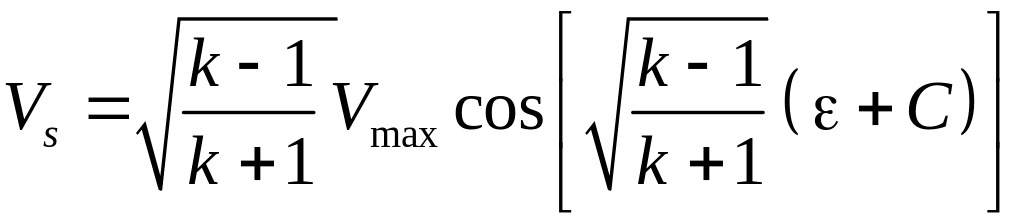 . (5.26)
. (5.26)
Для определения поля скоростей в области III (см. рис. 5.8) необходимо найти значение постоянной С. Воспользуемся граничным условием на линии возмущения ОВ.
При
![]() ,
,
![]() .
Поэтому
.
Поэтому
![]() и
и
![]()
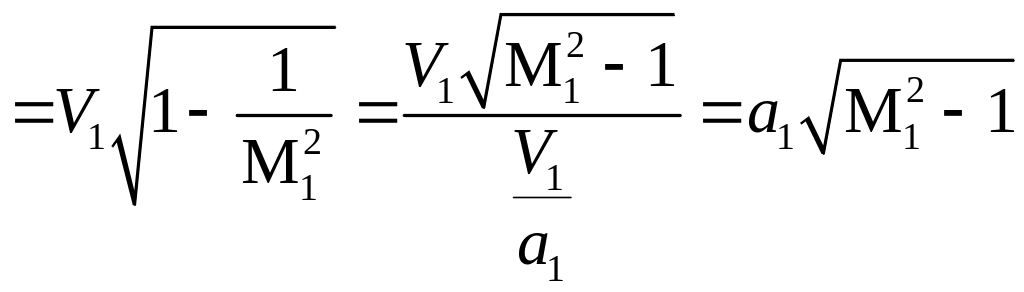 .
.
Отношение
скоростей
 с привлечением уравнений (5.25) и (5.26)
сводится к выражению
с привлечением уравнений (5.25) и (5.26)
сводится к выражению
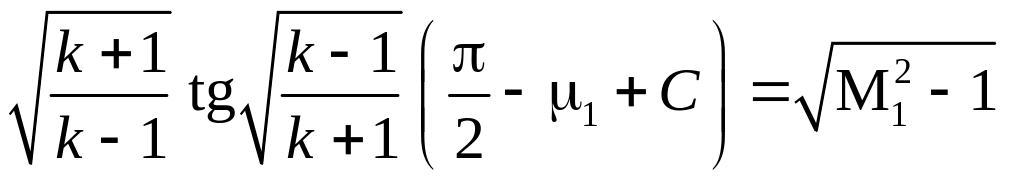 . (5.27)
. (5.27)
Так
как
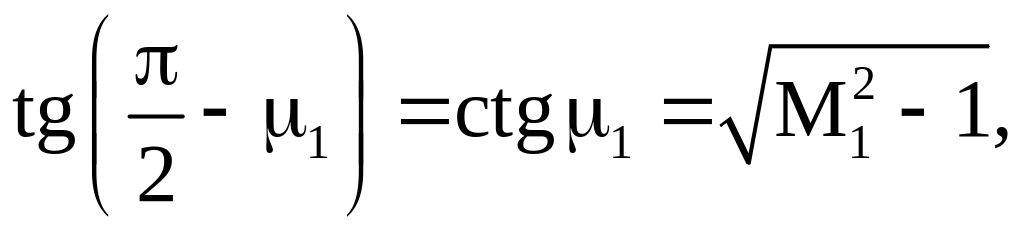 то
то
![]() и после преобразований выражения (5.27)
получим выражение для определения
произвольной постоянной:
и после преобразований выражения (5.27)
получим выражение для определения
произвольной постоянной:
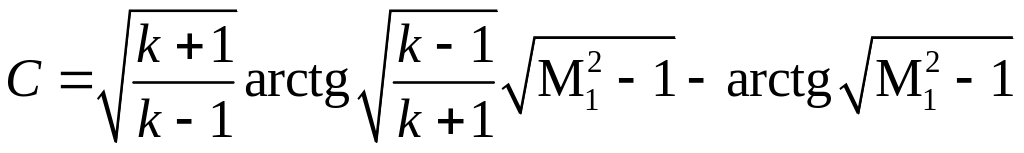 .
(5.28)
.
(5.28)
Значение
произвольной постоянной С
зависит от числа Маха набегающего потока
![]() .
При
.
При
![]() постоянная принимает значение С
= 0, в этом случае
постоянная принимает значение С
= 0, в этом случае
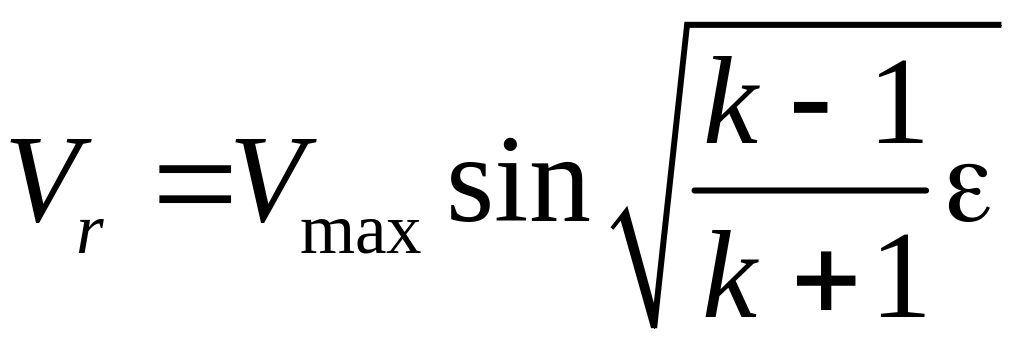 и
и
 .
.
Установим зависимость между углом поворота потока и числом М. По аналогии с выражением (5.27) найдем отношение скоростей для промежуточной характеристики ОЕ:
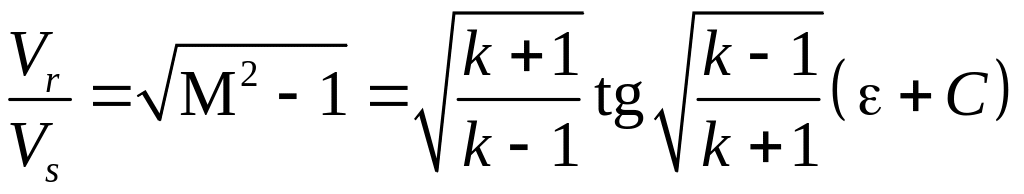 .
.
Отсюда
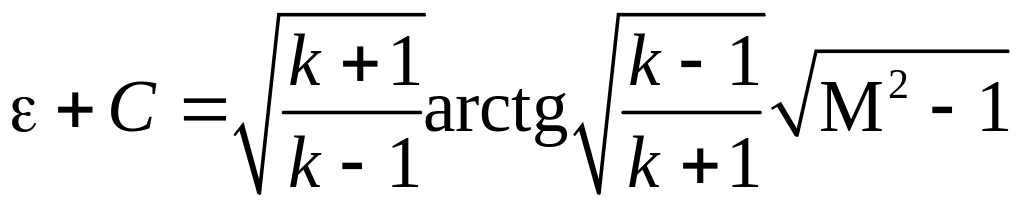 .
Для характеристики ОЕ
.
Для характеристики ОЕ
![]() ,
и учитывая, что
,
и учитывая, что
![]() ,
получим
,
получим
![]() .
.
Тогда зависимость угла поворота потока от числа Маха примет следующий вид:
 . (5.29)
. (5.29)
С равнение
формул для
и С
указывает на их абсолютную идентичность,
поэтому С
можно трактовать как угол
поворота звукового потока до получения
заданного числа
.
Поскольку этот поворот произошел вне
рамок данной задачи, то его принято
называть фиктивным
углом поворота
потока и обозначать через
равнение
формул для
и С
указывает на их абсолютную идентичность,
поэтому С
можно трактовать как угол
поворота звукового потока до получения
заданного числа
.
Поскольку этот поворот произошел вне
рамок данной задачи, то его принято
называть фиктивным
углом поворота
потока и обозначать через
![]() (рис. 5.9).
(рис. 5.9).
Тогда уравнение (5.29) примет вид
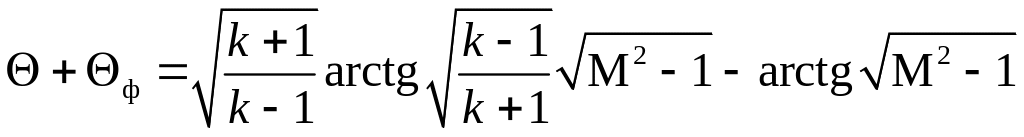 . (5.30)
. (5.30)
Это
уравнение совпадает с уравнением
эпициклоиды (5.19) (характеристики в
плоскости годографа скорости).
Следовательно, при обтекании угла,
большего
![]() по известной величине
можно найти скорость течения, пользуясь
сеткой эпициклоид.
по известной величине
можно найти скорость течения, пользуясь
сеткой эпициклоид.
Для
проведения инженерных расчетов составлены
таблицы изоэнтропических течений,
идущих с непрерывным увеличением
скорости. В основу положена
зависимость угла поворота потока (5.30)
от числа Маха после окончания разворота
(![]() ).
Поскольку каждому значению числа Маха
в начале разворота потока
).
Поскольку каждому значению числа Маха
в начале разворота потока
![]() соответствует свое значение фиктивного
угла
,
то при определении угла
поворота потока или
для каждого значения
пришлось бы иметь свои таблицы. Так как
расчетные формулы для угла поворота
потока и
абсолютно идентичны, то при составлении
таблиц учли это обстоятельство. В
таблицах приведены значения параметров
потока при повороте звукового (
= 1) потока на угол
.
Тогда при
> 1 сначала определяют
(из этих же таблиц) как угол поворота,
при котором происходит разгон потока
от М = 1 до М =
.
Затем по суммарному углу
соответствует свое значение фиктивного
угла
,
то при определении угла
поворота потока или
для каждого значения
пришлось бы иметь свои таблицы. Так как
расчетные формулы для угла поворота
потока и
абсолютно идентичны, то при составлении
таблиц учли это обстоятельство. В
таблицах приведены значения параметров
потока при повороте звукового (
= 1) потока на угол
.
Тогда при
> 1 сначала определяют
(из этих же таблиц) как угол поворота,
при котором происходит разгон потока
от М = 1 до М =
.
Затем по суммарному углу
![]() находят
и по соотношениям для изоэнтропических
течений рассчитывают другие параметры:
находят
и по соотношениям для изоэнтропических
течений рассчитывают другие параметры:
![]() .
.
Максимальный
угол поворота
![]() представляет собой угол поворота
звукового потока (
= 1, C
=
0) до получения им скорости
представляет собой угол поворота
звукового потока (
= 1, C
=
0) до получения им скорости
![]() (при
расширении до абсолютного вакуума, p
=
0
(при
расширении до абсолютного вакуума, p
=
0
![]() ).
Из уравне-ния
(5.30) при указанных условиях
).
Из уравне-ния
(5.30) при указанных условиях
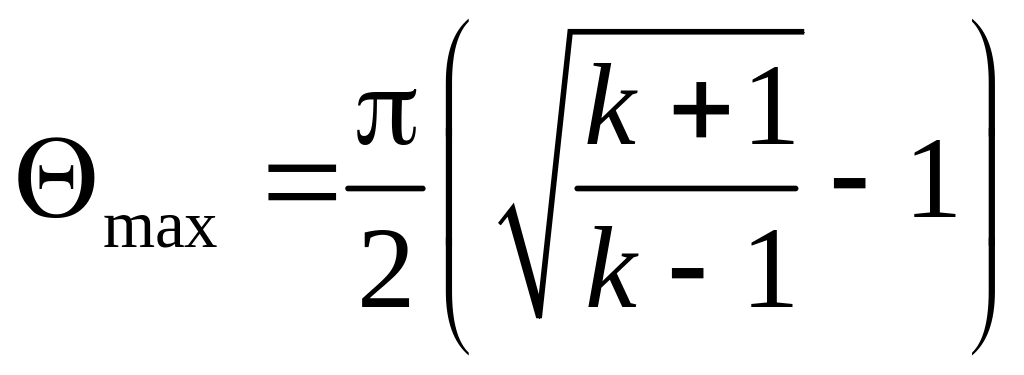 .
Для воздуха (k
=
1,4)
.
Для воздуха (k
=
1,4)
![]() .
.
Предельный
угол поворота
![]() – это угол, на который может повернуть
сверхзвуковой поток (
> 1) при его истечении в вакуум. В
соответствии с формулой (5.30)
– это угол, на который может повернуть
сверхзвуковой поток (
> 1) при его истечении в вакуум. В
соответствии с формулой (5.30)
![]() .
Для набегающего потока, число Маха
которого равно
= 1,
.
Для набегающего потока, число Маха
которого равно
= 1,
![]() ,
а для
=
,
а для
=
![]() ,
,
![]() .
.
Таким образом, рассмотренные сверхзвуковые течения с непрерывным увеличением скорости происходят плавно, без каких-либо особенностей. В то же время уменьшение скорости сверхзвукового потока и переход через скорость звука происходит скачкообразно.
