
- •Глава 5 плоские изоэнтропические течения газа
- •Основное дифференциальное уравнение плоского потенциального потока газа
- •Метод малых возмущений
- •Линеаризованное обтекание тупого угла сверхзвуковым потоком
- •Метод характеристик Метод характеристик позволяет рассчитать сверхзвуковое течение газа с помощью системы характеристик в плоскости потока и годографа скорости. Характеристики в плоскости потока
- •С. . Схема к задаче Коши
- •Обтекание сверхзвуковым потоком выпуклого угла (течение Прандтля–Майера)
- •Контрольные вопросы и задания
ДС. . Схема к задаче Коши
робь в правой части перед
![]() равна
равна
![]() ,
поэтому
,
поэтому
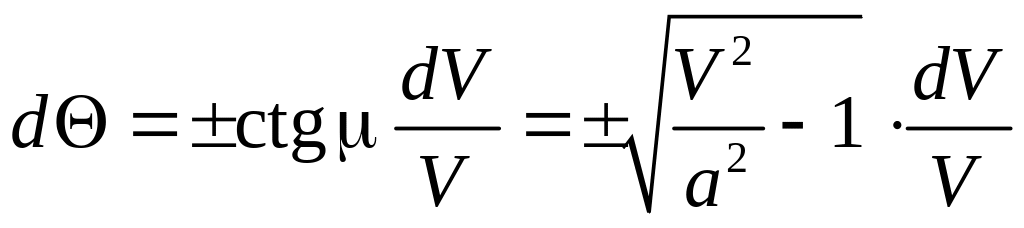 .
Представив скорость звука как
.
Представив скорость звука как
![]() ,
имеем следующее:
,
имеем следующее:
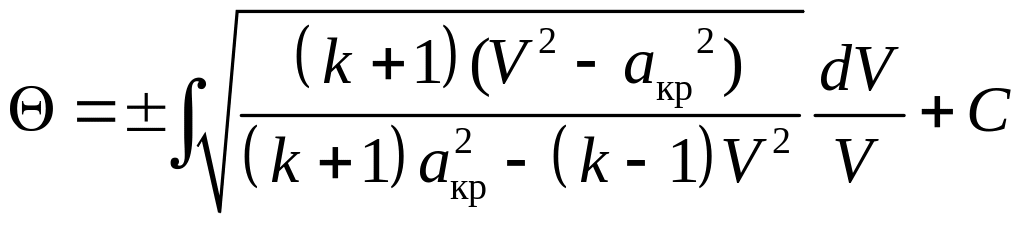 .
.
После
интегрирования, учитывая, что
![]() получим уравнение характеристик в
плоскости годографа скорости в конечном
виде:
получим уравнение характеристик в
плоскости годографа скорости в конечном
виде:
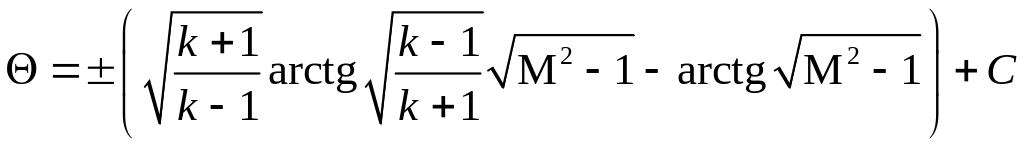 .
(5.19)
.
(5.19)
В этом уравнении
число Маха может изменяться в пределах
![]() ,
что соответствует изменению скорости
от
до
.
,
что соответствует изменению скорости
от
до
.
Кривые, описываемые этим уравнением, называются эпициклоидами. Через каждую точку плоскости проходит одна эпициклоида первого семейства и одна второго семейства. Задавая различные значения постоянной C, можно один раз вычертить сетку характеристик в плоскости годографа скорости и затем использовать ее при решении задач различного плана.
Таким образом, с помощью метода характеристик можно решать любые краевые задачи для сверхзвуковых потенциальных течений газа, если только найдены характеристики в плоскости XY течения газа и установлено их соответствие характеристикам в плоскости годографа . Таким образом, существо решения газодинамических задач методом характеристик состоит в поиске характеристик в плоскости течения газа.
Решение некоторых задач методом характеристик
Решим три задачи методом характеристик.
Задача 1 (Задача Коши)
Исходные данные: в физической плоскости XY на некоторой кривой АВ, которая не является характеристикой, задана скорость потока.
Т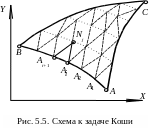 ребуется
определить:
скорости потока в области, ограниченной
этой кривой и двумя характеристиками
АС
и ВС
разных семейств (рис. 5.5), проведенных
из точек А
и В (эти
характеристики строятся при решении
задачи).
ребуется
определить:
скорости потока в области, ограниченной
этой кривой и двумя характеристиками
АС
и ВС
разных семейств (рис. 5.5), проведенных
из точек А
и В (эти
характеристики строятся при решении
задачи).
Решение:
рассмотрим на кривой АВ
ряд точек
![]() и проведем из каждой точки характеристики
(линии возмущения) обоих семейств до их
пересечения.
и проведем из каждой точки характеристики
(линии возмущения) обоих семейств до их
пересечения.
![]() – точки пересечения характеристик
разных семейств (узловые точки). Ввиду
малости участков разбиения характеристики
можно считать прямолинейными. Уравнение
отрезков этих прямых можно записать
как уравнения прямых, проходящих через
две точки:
– точки пересечения характеристик
разных семейств (узловые точки). Ввиду
малости участков разбиения характеристики
можно считать прямолинейными. Уравнение
отрезков этих прямых можно записать
как уравнения прямых, проходящих через
две точки:
![]() и
и
![]() (5.20)
(5.20)
Координаты
точек
определим из выражений (5.20). Так, точка
![]() есть точка пересечения характеристики
первого семейства, проведенной из точки
есть точка пересечения характеристики
первого семейства, проведенной из точки
![]() ,
и характеристики второго семейства,
проведенной из точки
,
и характеристики второго семейства,
проведенной из точки
![]() :
:
и
![]() .
(5.21)
.
(5.21)
Скорость
потока в узловых точках
![]() определим из уравнений соответствующих
характеристик в плоскости годографа
скорости, записанных через конечные
разности. Так для точки
они имеют вид
определим из уравнений соответствующих
характеристик в плоскости годографа
скорости, записанных через конечные
разности. Так для точки
они имеют вид
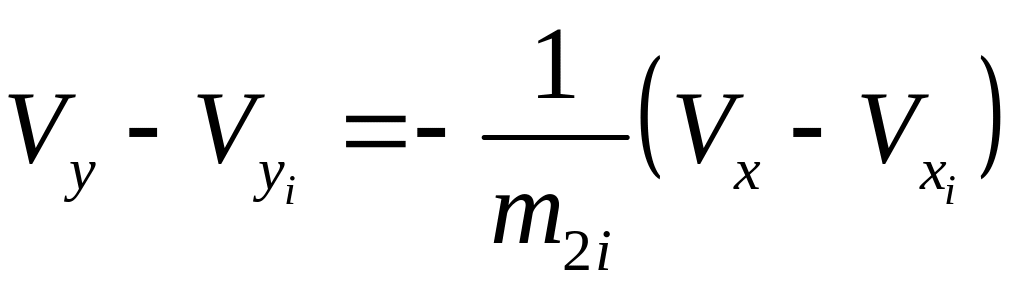 и
и
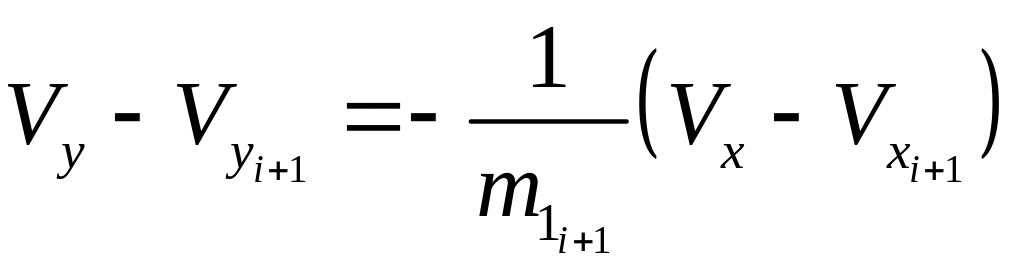 .
(5.22)
.
(5.22)
Система уравнений (5.21) позволяет определить координаты точ-ки . Решая систему уравнений (5.22). находим и в точке , а по ним и остальные параметры течения. Точно таким же образом определяются координаты всех других точек пересечения характеристик и находятся параметры течения в этих точках и т. д., пока не будут описаны подобным образом все точки рассматриваемой области течения. Крайние характеристики АС и ВС строятся в процессе решения задачи. Точность расчета зависит от количества выбранных точек на исходной кривой АВ (чем больше точек, тем выше точность).
Задача 2 (Задача Гурса)
Исходные данные: заданы скорости на двух характеристиках АВ и АС разных семейств, выходящих из точки А.
Т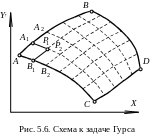 ребуется
определить:
поле скоростей в криволинейном
четырехугольнике (рис. 5.6), ограниченном
данными характеристиками и характеристиками
ВD
и СD,
исходящими из точек В
и С
(определенных в процессе решения задачи).
ребуется
определить:
поле скоростей в криволинейном
четырехугольнике (рис. 5.6), ограниченном
данными характеристиками и характеристиками
ВD
и СD,
исходящими из точек В
и С
(определенных в процессе решения задачи).
Решение:
Возьмем на АВ
и АС
ряд точек
![]() и
и
![]() .
Тогда угловую точку
.
Тогда угловую точку
![]() найдем как точку пересечения линий
возмущения разного семейства, проведенных
из точек
найдем как точку пересечения линий
возмущения разного семейства, проведенных
из точек
![]() (второго семейства) и
(второго семейства) и
![]() (первого семейства):
(первого семейства):
![]() ,
,
![]() .
.
Составляющие скорости в этой точке определим по уравнениям
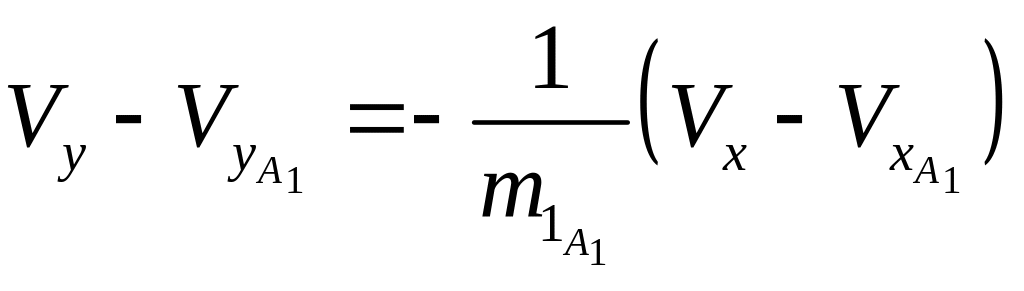 и
и
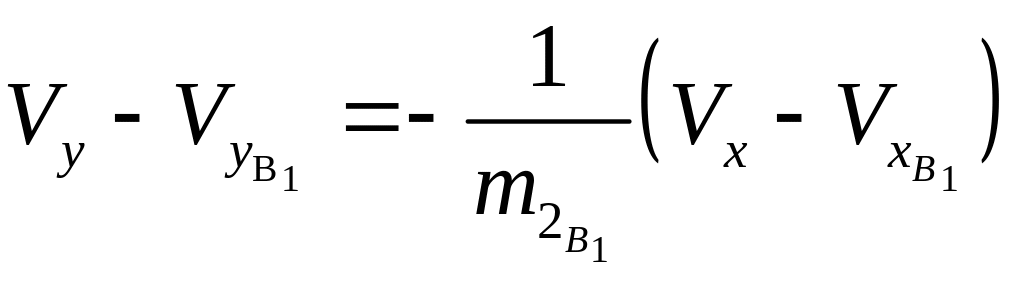 .
.
Затем
определим координаты и составляющие
скорости
для точки
![]() и т. д. для всей четырехугольной области
АВСD.
Определив величины составляющих
скорости, рассчитаем обычным порядком
остальные параметры течения.
и т. д. для всей четырехугольной области
АВСD.
Определив величины составляющих
скорости, рассчитаем обычным порядком
остальные параметры течения.
Задача 3
Исходные данные: заданы гидродинамические параметры на характеристике одного из семейств АВ и дана твердая стенка АС.
Требуется: определить параметры в треугольной области АВС (рис. 5.7), ограниченной твердой стенкой, заданной характеристикой АВ и характеристикой ВС, построенной в результате решения задачи.
Р ешение:
возьмем на характеристике АВ
ряд точек
.
Из точки
проведем линию возмущения второго
семейства до пересечения ее с твердой
стенкой в точке
ешение:
возьмем на характеристике АВ
ряд точек
.
Из точки
проведем линию возмущения второго
семейства до пересечения ее с твердой
стенкой в точке
![]() .
Координаты этой точки определим из
совместного решения уравнений линии
возмущения
.
Координаты этой точки определим из
совместного решения уравнений линии
возмущения
![]() и заданной поверхности стенки y
= y (x).
и заданной поверхности стенки y
= y (x).
В
точке
![]() направление скорости известно исходя
из следующих соображений. При безотрывном
обтекании стенки вектор скорости
направлен вдоль касательной к стенке
в точке
(условие непротекания). То есть
направление скорости известно исходя
из следующих соображений. При безотрывном
обтекании стенки вектор скорости
направлен вдоль касательной к стенке
в точке
(условие непротекания). То есть
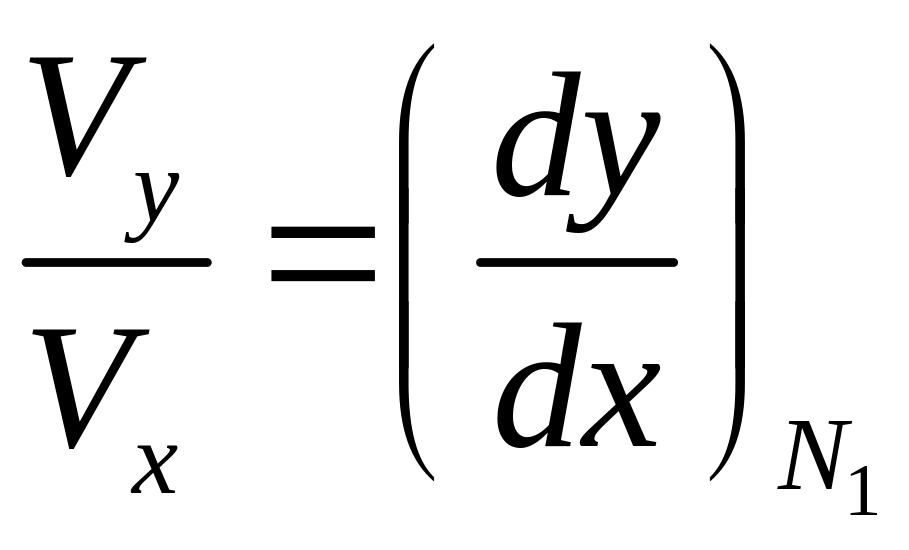 ,
и для нахождения составляющих скорости
используем уравнения
,
и для нахождения составляющих скорости
используем уравнения
и
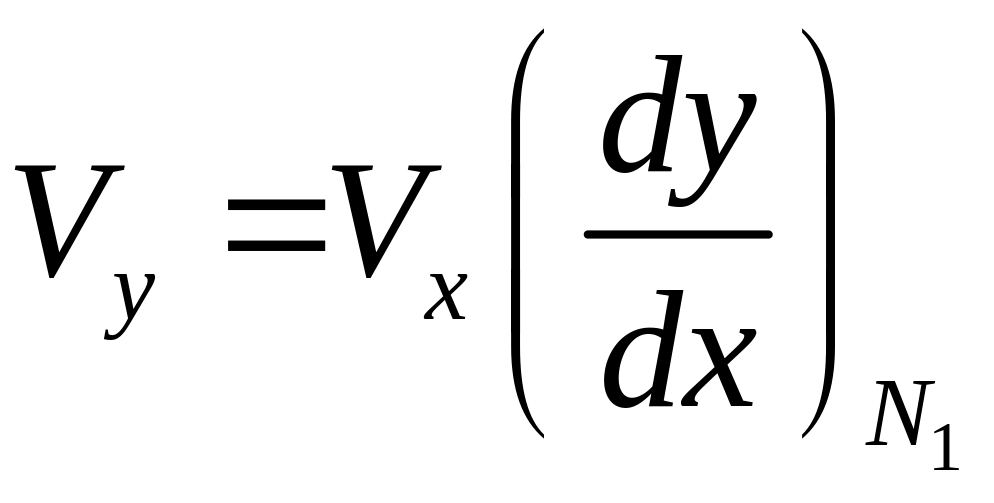 .
.
Затем,
зная
и
в точке
![]() и
,
находим координату точки
и составляющие скорости в ней, решая
задачу Гурса. Координаты точки
и
,
находим координату точки
и составляющие скорости в ней, решая
задачу Гурса. Координаты точки
![]() и значение скорости для нее определяем
так же, как и для точки
,
и далее определяем параметры течения
во всей искомой области АВС.
и значение скорости для нее определяем
так же, как и для точки
,
и далее определяем параметры течения
во всей искомой области АВС.
