Связь между скоростью течения газа и формой его струи

Для случая установившегося движения идеальной жидкости в трубке тока уравнение неразрывности можно записать в форме массового расхода .

Продифференцируем его и получим . Это выражение после его деления на равенство примет вид .

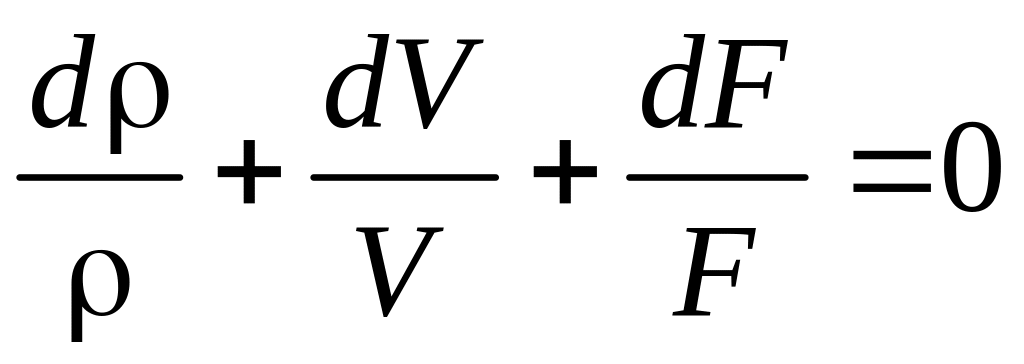Выразим через с помощью уравнения Бернулли и формулы для скорости звука (4.3): . Тогда исходное выражение после подстановки примет вид

, или . (4.21)

Уравнение (4.21) показывает, что связь между скоростью течения газа V и площадью поперечного сечения F имеет разный характер в зависимости от того, будет ли скорость течения больше или меньше скорости звука (рис. 4.8).

Если V < а, т. е. , то правая часть уравнения (4.21) будет отрицательной и знаки dF и dV будут, следовательно, разными. Это означает, что в дозвуковом потоке скорость газа меняется так же, как и в потоке несжимаемой жидкости, т. е. с увеличением площади поперечного сечения F скорость V убывает и наоборот (рис. 4.8, а, табл. 4.2).

Если же V > а, т. е. , то знак dF совпадает со знаком dV, иначе говоря, с увеличением F скорость V также увеличивается, а с уменьшением F – уменьшается (рис. 4.8, б). Такое явление в газе возможно потому, что увеличение скорости здесь сопряжено не только с понижением давления, как в несжимаемой жидкости, но и с разрежением, т. е. с уменьшением плотности. Расширение струек газа в сверхзвуковом течении ведет к расширению самого газа (в термодинамическом смысле), или к уменьшению давления, плотности и температуры и к увеличению скорости.

Таблица 4.2

Формы канала для разных случаев течения газа

Скорость течения	Форма насадка				Название насадка
Возрастает					Конфузор ( )
Уменьшается				Диффузор ( )

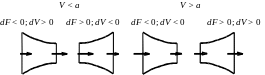
а б

Рис. 4.8. Изменение скорости вдоль канала:

а – в дозвуковом потоке; б – в сверхзвуковом потоке

П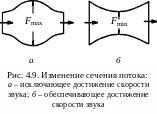 ри V = а dF = 0. При непрерывном изменении скорости течения (т. е. при ) это условие может быть реализовано только в экстремальном, а именно в минимальном, сечении потока (рис. 4.9). Действительно, если в начале расширяющейся части потока (рис. 4.9, а) скорость меньше скорости звука а, то она будет уменьшаться в направлении течения. В противном случае если на входе V будет больше а, то скорость течения увеличится. В обоих случаях при переходе через скорость течения никак не может сравняться со скоростью звука.

Наоборот, в сужающемся участке потока (рис. 4.9, б) дозвуковая скорость будет увеличиваться, а сверхзвуковая – уменьшаться, и в обоих случаях достижение скорости звука возможно. Сечение потока, в котором скорость течения V достигает скорости звука а ( ), называют критическим. Для газовой струи критическим сечением является ее минимальное сечение.

Эту особенность газовых струй учитывают при проектировании специальных насадков (сопел), которые должны обеспечивать истечение газа со сверхзвуковой скоростью.