
- •Глава 4 одномерные изоэнтропические течения газа
- •Распространение малых возмущений. Скорость звука
- •Основные соотношения для одномерных изоэнтропических потоков газа
- •Величины числа Маха и коэффициента скорости при характерных значениях скорости V
- •Газодинамические функции
- •Связь между скоростью течения газа и формой его струи
- •Формы канала для разных случаев течения газа
- •Сверхзвуковое сопло (сопло Лаваля)
- •Режимы работы сверхзвукового сопла
- •Контрольные вопросы и задания
Величины числа Маха и коэффициента скорости при характерных значениях скорости V
Скорость потока
|
0 |
|
|
Число Маха
|
0 |
1 |
|
Коэффициент
скорости
|
0 |
1 |
|
Отношение квадратов
скоростей
с учетом формулы (4.12) можно записать как
 и
и

 .
Отсюда получаем зависимость коэффициента
скорости от числа Маха:
.
Отсюда получаем зависимость коэффициента
скорости от числа Маха:
 .
(4.17)
.
(4.17)
Тогда формулы (4.9) можно представить через коэффициент скорости в виде
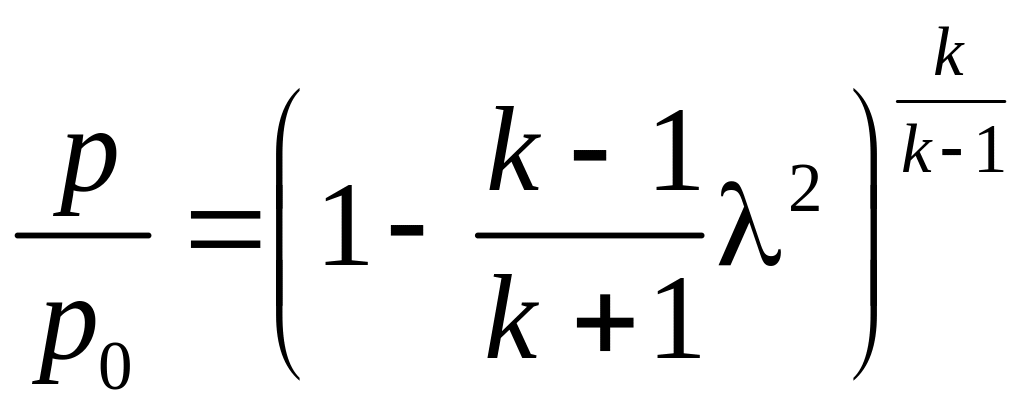 ,
,
 ,
,
 (4.18)
(4.18)
Ф
 ормулы
(4.16), (4.16а) и (4.18) показывают, что с ростом
чисел М и
ормулы
(4.16), (4.16а) и (4.18) показывают, что с ростом
чисел М и
![]() величины параметров
уменьшаются и в пределе их значения
стремятся к нулю, что может быть
справедливо только для идеального
газа.
величины параметров
уменьшаются и в пределе их значения
стремятся к нулю, что может быть
справедливо только для идеального
газа.
Формула (4.16) имеет большое практическое значение для нахождения числа М в дозвуковом потоке (в дозвуковых АДТ). Определяя экспериментально давление торможения и статическое давление в потоке p с помощью специального насадка – трубки Пито–Прандтля (рис. 4.6), по формуле (4.16) можно рассчитать число Маха набегающего потока.
Газодинамические функции
Мы установили
количественные соотношения между
текущими значениями
![]() и их величиной для заторможенного газа
(параметрами торможения). Эти уравнения
содержат М и
в высоких и дробных степенях, поэтому
их преобразование, получение явных
зависимостей между параметрами в общем
виде представляет трудности (при
современном состоянии программного
обеспечения и вычислительной техники
все делается довольно просто в численном
виде). Рассматривая уравнения газового
потока, можно заметить, что величины М
и
входят в них в виде нескольких часто
встречающихся комбинаций (выражений),
которые получили название газодинамических
функций.
Этим функциям присвоены сокращенные
обозначения, и их значения в зависимости
от М,
и
вычислены и сведены в таблицы.
и их величиной для заторможенного газа
(параметрами торможения). Эти уравнения
содержат М и
в высоких и дробных степенях, поэтому
их преобразование, получение явных
зависимостей между параметрами в общем
виде представляет трудности (при
современном состоянии программного
обеспечения и вычислительной техники
все делается довольно просто в численном
виде). Рассматривая уравнения газового
потока, можно заметить, что величины М
и
входят в них в виде нескольких часто
встречающихся комбинаций (выражений),
которые получили название газодинамических
функций.
Этим функциям присвоены сокращенные
обозначения, и их значения в зависимости
от М,
и
вычислены и сведены в таблицы.
Расчет газовых потоков с помощью таблиц газодинамических функций получил широкое применение в лабораторной практике.
Приведем простейшие функции, которые выражают связь между параметрами газа в потоке и параметрами торможения:
 ,
,
 ,
,
 .
(4.19)
.
(4.19)
Указанные соотношения связывают между собой параметры газа в одном и том же сечении потока.
Обычно в таблицах
независимым параметром считают
,
и ему ставят в соответствие значения
числа М и газодинамических функций.
Газодинамические функции
![]() связаны между собой через уравнение
состояния
связаны между собой через уравнение
состояния
![]() :
:
![]() .
.
Функции, позволяющие выразить расход газа, выглядят следующим образом:
через полное давление
![]() (4.20)
(4.20)
через статическое давление:

где
константа
 (для воздуха
).
(для воздуха
).
Ф ункция
ункция
![]() (рис. 4.7) имеет особенность, которая
заключается в том, что одному и тому же
значению
отвечают два значения скорости. Первое
из них – в диапазоне дозвуковых, а второе
– в диапазоне сверхзвуковых скоростей.
Поэтому при определении числа Маха или
коэффициента скорости по газодинамическим
таблицам эту особенность необходимо
помнить. С помощью функций
и
(рис. 4.7) имеет особенность, которая
заключается в том, что одному и тому же
значению
отвечают два значения скорости. Первое
из них – в диапазоне дозвуковых, а второе
– в диапазоне сверхзвуковых скоростей.
Поэтому при определении числа Маха или
коэффициента скорости по газодинамическим
таблицам эту особенность необходимо
помнить. С помощью функций
и
![]() получим два выражения для расхода:
получим два выражения для расхода:
 ,
,
где B – постоянный коэффициент, зависящий от физических свойств данного сорта газа (его величина для воздуха равна 0,0405). Получить выражение для В в общем виде читатели могут самостоятельно.
Функции, при помощи которых импульс газового потока выражается через полное и статическое давление, следующие:
![]() и
и
 .
.
Соответственно, получаем два выражения для расчета импульса газового потока:
 .
.
