Глава 4 одномерные изоэнтропические течения газа

Так как сжатие (расширение) газа сопровождается повышением (понижением) давления, то, следовательно, газ обладает свойствами упругого тела. Местное уплотнение малой интенсивности ( , ) будет распространяться в виде возмущения (изменения состояния), называемого волной, с некоторой скоростью . Такова же природа и звуковой волны, представляющей собой продольные волны малой интенсивности. Поэтому скорость распространения любых малых возмущений в газе равна скорости звука.

Распространение малых возмущений. Скорость звука

Поверхность, отделяющая область возмущений от невозмущенной области, называется фронтом волны. В однородной среде волны малой интенсивности распространяются с одинаковой скоростью во всех направлениях, и фронт волны представляет собой сферическую поверхность (сферическую волну).

П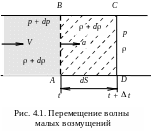 олучим формулу для расчета скорости звука. Зафиксируем два положения волны (рис. 4.1): за промежуток времени волна из положения AB переместилась в положение CD, пройдя расстояние . То есть скорость звука (скорость распространения волны возмущения) равна .

Сжимаемая среда за счет возмущения давления будет двигаться с малой скоростью . Возрастание плотности в области ABCD на величину происходит за счет втекания газа в область возмущения с этой скоростью. Масса газа, втекающего в объем ABCD, равна . Этот прирост массы в объеме ABCD равен . Тогда , и, учитывая, что , получим

. (4.1)

С другой стороны, импульс силы , вызвавший приток массы газа, должен быть равен изменению количества движения жидкости в области ABCD. Следовательно, , или . Учитывая выражение (4.1), имеем следующее: , т. е.

(4.2)

Отсюда следует, что скорость звука зависит от закона, связывающего изменение давления с изменением плотности. П. Лаплас показал, что звуковые колебания распространяются достаточно быстро, и теплообмен с окружающей средой не успевает произойти. Процесс распространения звуковых волн можно считать адиабатическим. Для адиабатического процесса . Тогда и формула для расчета скорости звука будет иметь вид

. (4.3)

Для воздуха , и скорость звука равна

. (4.4)

Рассмотрим, как распространяются волны малых возмущений при различных скоростях движения среды. Пусть точечный источник возмущений расположен в точке О (рис. 4.2). Если газ покоится ( ), то возмущения в моменты времени и т. д. образуют ряд концентрических сферических волн с центрами в точке О и радиусом от нуля до аt_i на рассматриваемом отрезке времени.

µ

а б

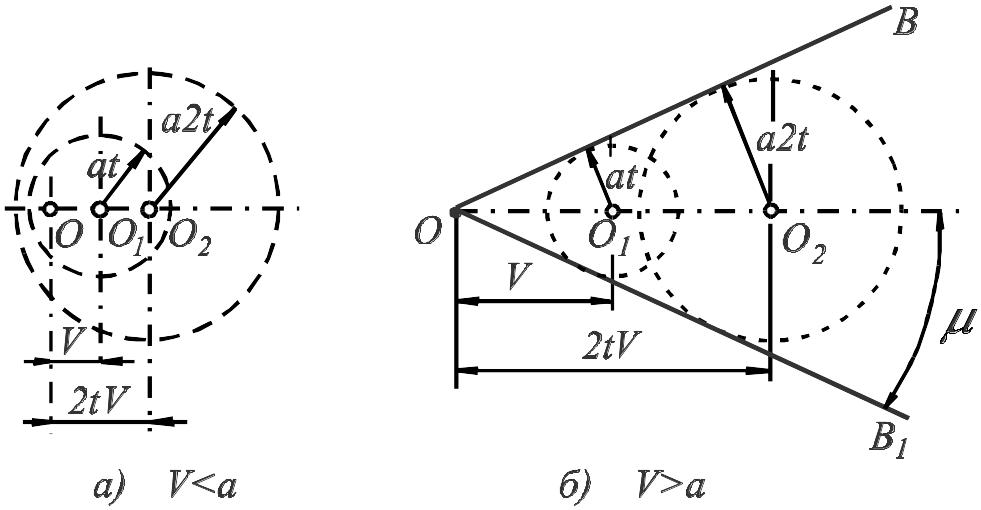
Рис. 4.2. Распространение слабых возмущений:

а – в дозвуковом потоке (V < а); б – в сверхзвуковом потоке (V > а)

Если источник возмущений движется с некоторой скоростью (или поток движется относительно источника возмущений), то картина распространения возмущений изменяется.

При движении точечного источника возмущений с дозвуковой скоростью V < а сферические волны смещаются в сторону источника, но опережают его, т. е. источник находится внутри сферической волны, вызванной этим телом (рис. 4.2, а). При звуковой скорости источника передний край волны возмущения и положение источника совпадают.

Когда скорость источника возмущений становится больше скорости распространения волны (V > a), тело обгоняет волны, оставляя их позади себя в виде расширяющегося конуса, вершиной которого является само тело (рис. 4.2, б). Возмущения при сверхзвуковых скоростях навстречу потоку не распространяются, т. е. не проникают вперед в невозмущенную область.

Этот конус является огибающей сферических волн возмущений и называется конусом возмущения, или конусом Маха. Конус возмущений разделяет области возмущенного и невозмущенного потока. Если этот конус рассечь плоскостью, проходящей через его ось, то можно получить прямые OB и OB₁, называемые линиями возмущений (линиями Маха), которые являются ударными волнами бесконечно малой интенсивности. Угол , равный половине угла при вершине конуса, называется углом возмущений. Этот угол связан со скоростью движения тела и скоростью звука зависимостью

или , (4.5)

где М – число Маха, – местная скорость потока; – местная скорость звука.

При  = /2 sin  = 1 и M = 1, т. е. V = а (скорость источника равна скорости звука). Из уравнения (4.5) видно, что с увеличением числа М уменьшается угол наклона линий слабых возмущений, т. е. зона возмущений сужается.