Глава 2 основы кинематики сплошной среды

Движение сплошной среды характеризуется, прежде всего, скоростями ее частиц. В каждый момент времени каждая частица имеет определенную по величине и по направлению скорость.

Если поле скоростей неизменно во времени, то движение называется стационарным (установившимся), если оно зависит от времени – нестационарным (в некоторых точках пространства движущейся жидкости характер движения зависит от выбора системы координат: связанной с телом или неподвижной).

В практике часто используют понятие средней скорости. Усреднение скорости производят либо по времени, либо по площади некоторого сечения потока.

Среднее значение скорости за промежуток времени представляет собой интеграл . Средняя величина скорости по некоторой площади определится как .

Вектор ускорения жидкой частицы, движущейся со скоростью V, является индивидуальной производной по времени от вектора скорости .

Методы описания движения жидкости

Задача кинематического изучения движения жидкости заключается в определении в каждой точке движущегося газа значения скорости для любого момента времени.

Движение газа можно изучать двумя методами – методом Эйлера или методом Лагранжа.

Метод Эйлера. В методе Эйлера фиксируется точка пространства с координатами x, y, z и исследуется изменение скорости частиц в этой точке с течением времени. Отслеживаемая скорость частиц является функцией координат и времени V = ƒ (t, x, y, z). Совокупность величин x, y, z, t называется переменными Эйлера.

Движение газа по методу Эйлера задается следующим образом:

(2.1)

Предполагая движение газа непрерывным, будем считать указанные функции однозначными, непрерывными и дифференцируемыми функциями координат x, y, z и времени t. В этом случае для нахождения траектории частиц газа следует в уравнениях (2.1) заменить на производные и интегрировать следующую систему дифференциальных уравнений:

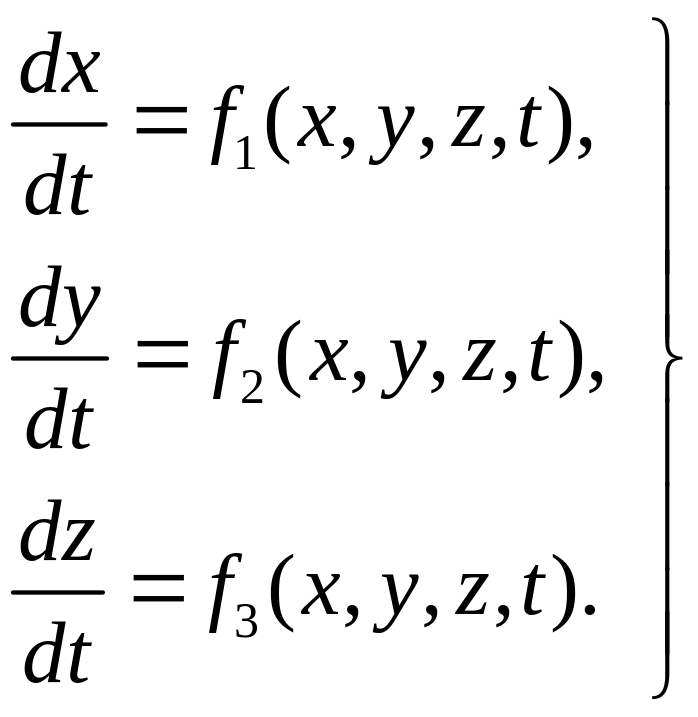(2.2)

После интегрирования системы (2.2) получим

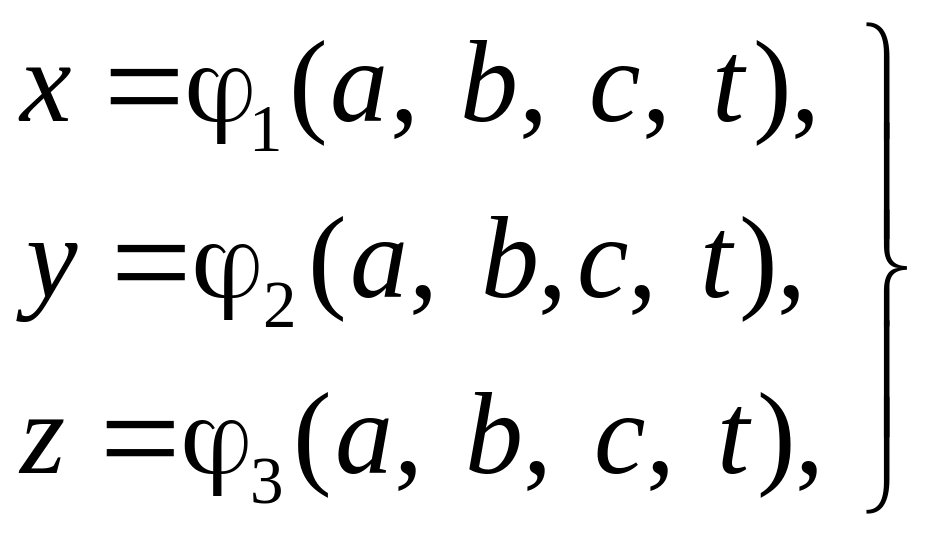
где a, b, c – произвольные постоянные, значения которых определяются исходя из начальных условий. Исключим время t и получим уравнение траектории частицы газа.

Проекции ускорения газовых частиц в переменных Эйлера следующие:

где – функции от x, y, z; x, y, z – функции от t.

По правилу дифференцирования сложной функции

. (2.3)

Так как , то выражения для проекций ускорения запишутся в виде

Следует помнить, что когда берутся полные производные, то учитывается не только изменение времени t, но и изменение координат (в зависимости от времени – x(t), y(t), z(t)) частицы газа при ее движении по траектории. Частные производные называются конвективными. Конвективная производная отражает то обстоятельство, что скорость движения изменяется при перемещении из одной точки пространства в другую. Конвективное ускорение имеет место практически всегда при стационарном и нестационарном движениях. Оно может быть равно нулю только тогда, когда .

Частные производные по времени берутся при фиксированных значениях координат и называются локальными (местными) производными. Локальная производная характеризует нестационарность процесса. При стационарном движении локальное ускорение всегда равно нулю. При нестационарном движении оно равно нулю только тогда, когда в данной точке скорость имеет экстремальное (максимальное или минимальное) значение во времени.

Метод Лагранжа. В методе Лагранжа фиксируются индивидуальные частицы газа и рассматривается их движение вдоль собственных траекторий. Так как газовых частиц бесчисленное множество, то охарактеризуем каждую частицу. В качестве характеристики частицы выберем ее координаты в начальный момент времени t = t₀ (a, b, c). Это означает, что из всей совокупности траекторий данной частице будет принадлежать та, которая проходит через точку a, b, c. Таким образом, координаты данной частицы x, y, z зависят от a, b, c, t – переменных Лагранжа, т. е.

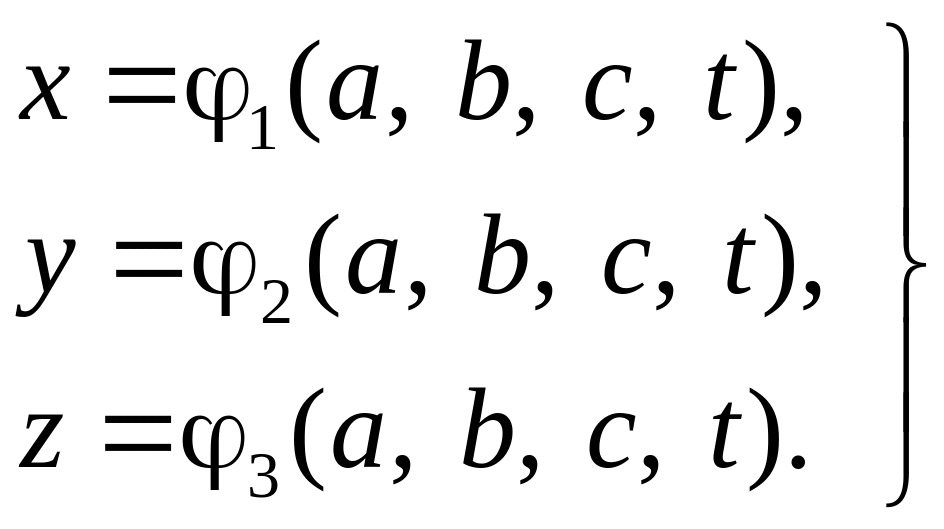. (2.4)

Уравнения (2.4) – это параметрические уравнения семейства траекторий, заполняющих все пространство, занятое газом.

Таким образом, если в методе Эйлера траектории движения частиц получаются интегрированием дифференциальных уравнений (2.2), то в методе Лагранжа они заданы функциями (2.4), из которых могут быть найдены проекции скорости и ускорения частиц:

, ,

, ,

, .

Однако для решения большинства практических задач аэродинамики нет необходимости знать траектории движения частиц. Чаще всего нужно иметь данные о величине скорости в данной точке пространства вне зависимости от индивидуальности частицы, проходящей через нее. Этим практическим вопросам отвечает метод Эйлера, который как наиболее простой чаще всего применяется в аэродинамике.