4.2. Измерение температуры газа в потоке назад

При движении газа с большими скоростями, когда влияние сжимаемости становится заметным, различают статическую температуру Т_ст и температуру торможения Т₀.

Статическая температура – это температура газа в рассматриваемой точке. Эту температуру покажет прибор (термометр), движущийся вместе с частицами газа при отсутствии излучения.

Т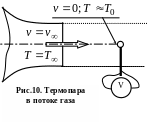 емпература торможения – это температура, которую имеет адиабатический заторможенный в данной точке поток. Эту температуру измерил бы датчик (термопара) (рис.10) в критической точке при отсутствии потерь тепла в окружающей среде. Создать такой датчик практически невозможно. Поэтому датчик температуры, помещенный в поток, измерит некоторую температуру , близко к . Датчик температуры характеризуется коэффициентом восстановления

.

Коэффициент восстановления учитывает теплообмен через газообразную среду, через материал насадка и крепления, а также излучение датчика. Коэффициент  определяют при помощи специальной градуировки датчика в аэродинамической трубе. Непосредственно измерить статическую температуру потока Т_cт практически невозможно. Зная температуру , измеренную датчиком, и его коэффициент восстановления, можно найти температуру торможения по формуле

где , М – местное число Маха.

Для измерения температуры газа применяют термопары железо-константан, хромель-коппель, хромель-алюмель. Величина ЭДС, пропорциональная температуре, измеряется милливольтметром. Для этой же цели применяться термометры сопротивления.

При малых скоростях потока измерение температуры с достаточной точностью производится обычным воздушным термометром, помещенным в форкамере трубы.

4.3. Теоретические основы измерения скорости дозвукового потока назад

В методике измерения скорости существует два приема. Первый может быть назван анемометрическим, а второй – пневмометрическим. Анемометр – это прибор, непосредственно измеряющий величину скорости. Пневмометр позволяет измерить скорость не непосредственно, а путем измерения давления, соответствующего измеряемой скорости. Основным способом определения скорости потока при аэромеханических исследованиях является пневмометрический из-за своей универсальности и ряда преимуществ.

Для измерения скорости дозвукового потока главным образом применяются косвенные методы, основанные на различных физических эффектах, вызываемых движением среды, или на связи скорости или числа Маха с другими параметрами потока, поддающимися измерению. Для изоэнтропического течения число Маха можно найти, воспользовавшись любым из соотношений:

, или .

Требуется лишь знать пару входящих в каждое из этих уравнений параметров заторможенной и движущейся жидкости (температуры, плотности или давления). Начальные параметры заторможенной жидкости и , остающиеся неизменными во всем поле изоэнтропического течения, сравнительно легко поддаются непосредственному измерению, например, в форкамере аэродинамической трубы, где скорость потока мала. Зная и , с помощью уравнения состояния можно найти . Относительно статических значений параметров потока следует иметь в виду, что в настоящее время нет метода, позволяющего осуществить непосредственное измерение и . Определить можно путем измерения скорости распространения звуковых волн, которая зависит от температуры газа и его физических свойств: . Однако скорость звука и, следовательно, температуру газа в точке потока определить невозможно, так как излучатель и приемник звуковых волн должны находиться на некотором, известном расстоянии друг от друга. Плотность в потоке сжимаемой жидкости можно определить, пользуясь косвенными методами, основанными на связи плотности с коэффициентами преломления, поглощения или излучения среды. Связанные с коэффициентом преломления оптические методы измерения плотности позволяют исследовать поле в возмущенных областях изоэнтропических и неизоэнтропических течений. Из всех трех статических параметров , и непосредственному измерению поддается лишь статическое давление . Поэтому основным, наиболее точным методом определения числа Маха и скорости потока вплоть до больших сверхзвуковых скоростей, является так называемый пневмометрический метод, основанный на измерении давления.

Используя уравнение Бернулли, выведенное в предположении, что газ сжимаем, можно получить формулу для определения числа Маха при изоэнтропическом течении в виде:

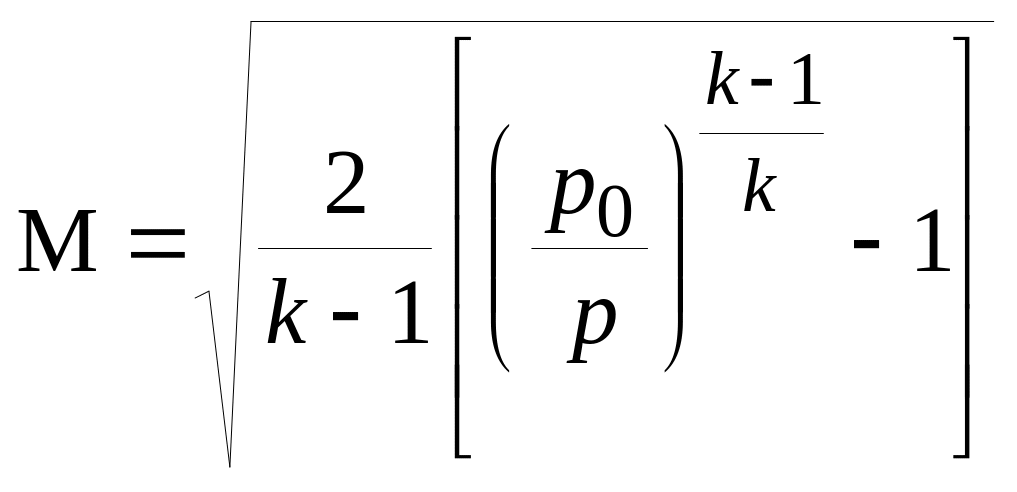(1)

На основе зависимости скорости звука от температуры и, учитывая, что , получим:

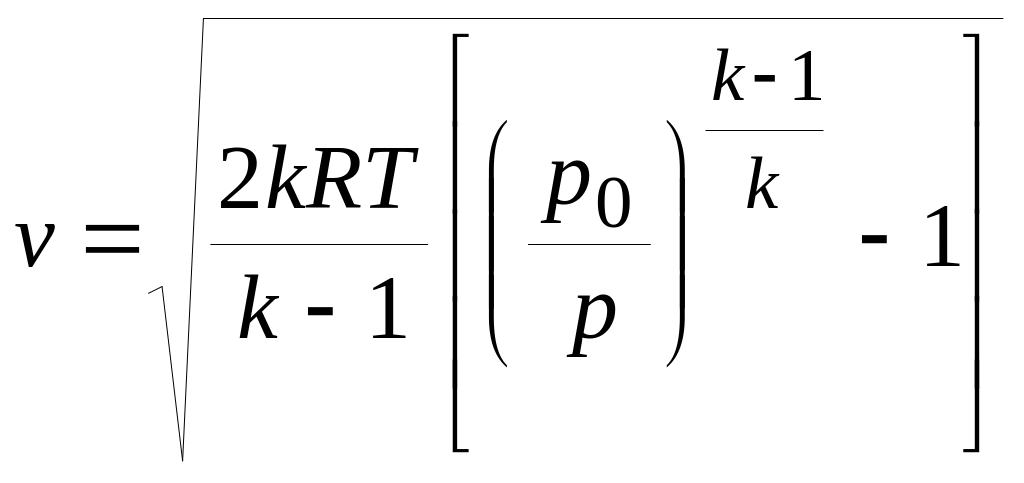(2)

Проанализировав (2) видим, что для определения скорости по значениям давлений требуется измерить три местных параметра , и . Так как измерение затруднительно, то местную температуру определяют, измеряя значение , и в формулу (2) подставляют величину .

Решая уравнение (1) относительно с использованием разложения в биноминальный ряд по степени , получим

, (3)

или , (4)

где .

При k = 1,4 выражение для будет иметь вид:

(5)

Формула (4) справедлива при числах Маха М < 1. Если число М достаточно мало, то , и уравнение (4) превращается в уравнение Бернулли для несжимаемой жидкости:

(6)

Для расчета скорости потока несжимаемой жидкости по формуле (6) достаточно измерить величину . Сравнивая выражения (4) и (6), замечаем, что величина представляет собой погрешность расчета давления без учета сжимаемости, отнесенную к скоростному напору. Значения в зависимости от скорости (числа М) для воздуха (k = 1,4), вычисленные по формуле (5), даны табл. 2.

Таблица 2

Погрешность расчета давления без учета сжимаемости среды

, м/с	34	68	102	136	170	204	238	272	306	340
М	0,1	0,2	0.3	0.4	0.5	0,6	0,7	0.8	0,9	1.0
, %	0,25	1.0	2,25	4.0	6.2	9,0	12,8	17,3	21,9	27,5

Относительная величина ошибки в измерении скорости при пренебрежении сжимаемостью (рис.11) равна: , где определяется по (6), а - по (4): . Учитывая (5), получаем (7)

Аналогично можно представить зависимость изменения плотности сжимаемой среды:

(8)

Согласно (5), (7) и (8) и табл. 2 видно, что сжимаемость воздуха уже при числе Маха М = 0,2 вносит погрешность в определение давления равную 1 %, а в определение скорости – равную 0,5 %. Кроме того, сжимаемость сильнее влияет на плотность, чем на скорость. При скоростях до 100 м/сек для определения скорости по измеренным давлениям можно воспользоваться формулой (6), а при скоростях превышающих 100 м/сек – формулой (4).

В еличина , называемая скоростным напором набегающего потока, имеет большое значение в экспериментальной аэродинамике. При определении безразмерных аэродинамических коэффициентов к величине скоростного напора набегающего потока относят значения сил и давлений, действующих на исследуемые в аэродинамических трубах модели.

Согласно (4) и (5), для сжимаемой жидкости величина , больше скоростного напора, , т.к. и .