7. Определение поля скоростей в рабочей части аэродинамической трубы

Поток газа, сформированный соплом аэродинамической трубы с открытой рабочей частью, обладает всеми свойствами затопленных струй. На рис.14 приведен пример поля скоростей в одном из сечений рабочей части. Как видно, в рабочей части трубы имеется значительная область равномерных прямолинейных скоростей – ядро потока, где может быть помещено испытуемое тело. От ядра потока к границам скорость падает до нуля. При проектировании АДТ важно стремиться к тому, чтобы ядро потока имело наибольшую протяженность. Поле скоростей трубы не должно заметно изменяться при переходе от одного сечения рабочей части к другому. Для характеристики равномерности поля скоростей используют безразмерный коэффициент поля скоростей , где – местная скорость в некоторой точке, – среднее значение скорости по сечению.

Ч аще величину определяют как отношение местной скорости в выбранной точке к скорости в фиксированной точке расположения контрольного насадка или к скорости , измеренной по перепаду давления. Тогда или

(14)

Среднее значение коэффициента поля в сечении рабочей части трубы можно рассчитать по формуле

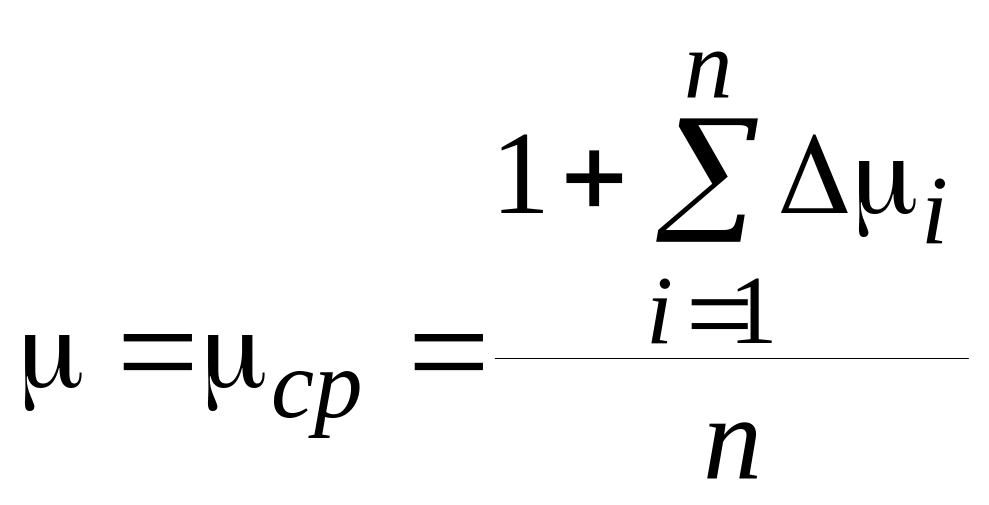, (15)

где , а – число точек сечения.

В трубах малых скоростей поле потока, как правило, обследуют одним насадком Пито-Прандтля, установленным на координатнике. Измерения обычно начинают в средней точке выбранного сечения, а затем, перемещая насадок в вертикальном направлении (вдоль оси ОУ) с некоторым шагом, равным примерно 0,05…0,1 сечения потока, определяют для соответствующих точек с координатами значения скоростных напоров. Аналогичные измерения осуществляют, перемещая насадок в горизонтальном направлении. Так как определение местных скоростей не может быть проведено при такой способе во всех намеченных точках одновременно, то может оказаться, что они будут соответствовать разным значениям скорости набегающего потока и, следовательно, эту скорость необходимо также определять при каждом отсчете местной скорости. Для этого используют метод определения скорости потока контрольным приемником давления или метод перепада давления. Величины скоростей и вычисляют по формулам (10) и (13) соответственно.

Обычно экспериментальные исследования ограничивают измерением скоростей в точках на взаимно перпендикулярных осях симметрии какого-либо сечения, что бывает достаточно для оценки равномерности потока. Для определения геометрии ядра потока в рабочей части необходимо измерить профили скорости по минимуму в двух поперечных сечениях, удаленных на значительное расстояние друг от друга.

Диаграмма испытания строится в произвольном, но удобном для чтения масштабе. При построении зависимостей обычно используют безразмерные координаты. Например, для описанной выше экспериментальной установки: , , где мм – ширина потока на срезе сопла.

8. Математическая обработка результатов эксперимента назад

После окончания эксперимента необходимо выполнить требуемые расчеты, провести анализ результатов эксперимента и сделать выводы.