3.2.5. Автоматы и языки

Рассмотрим ряд базовых определений.

Пусть V есть произвольный алфавит, а v есть буква в V. Назовем словом в V всякую последовательность букв из V. Число вхождений букв в слово назовем длиной слова. Пустое слово (слово длины 0) обозначим через L.

Множество всех слов длины n обозначим через . Множество всех слов (слов всевозможных длин) обозначим через , т.е. = L È È È È…

Языком в алфавите V назовем всякое подмножество L слов в этом алфавите, L Î .

Рассмотрим на множестве слов операцию конкатенации слов, определяемую как приписывание одного слова к другому. Пусть α, β Î и α = aba, β = aa, то конкатенация α.β = abaaa.

Назовем источником всякую диаграмму в алфавитах U и V, в которой выделены два подмножества вершин 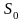, S Í U. Вершины из называются начальными, а из S – финальными.

Рассмотрим произвольный маршрут из вершины , Î , в вершину s, s Î S. Выпишем последовательность меток дуг этого маршрута в порядке прохождения дуг, получим слово в алфавите V.

Будем говорить, что слово несомо данным маршрутом или что данный маршрут несет слово.

Рассмотрим множество всех маршрутов из вершин множества в вершины множества S. Множество слов, несомых этими маршрутами, образуют язык. Будем говорить, что этот язык представляется данным источником.

На одной и той же диаграмме с помощью различных пар < , S> можно представлять различные языки.

Перенесем введенные понятия на автоматные диаграммы.

Пусть A = <X, Q, ψ> есть автомат без выхода, в котором выделено начальное состояние и множество S финальных состояний, S Í Q.

Тройку <A, , S> будем называть настроенным автоматом, а пару < , S> – его настройкой.

Язык L(A, , S) есть язык, представленный настроенным автоматом <A, , S>. Этот язык удобно задавать соответствующим настроенным источником в алфавитах Q, X.

На одной и той же автоматной диаграмме переходов с помощью различных пар < , S> (различных настроек диаграммы) можно задавать различные языки.

Произвольный язык L Í называется конечноавтоматным языком, если существует конечный настроенный автомат <A, , S>, представляющий этот язык.

3.2.6. Операции над конечноавтоматными языками

Перечислим основные операции над языками.

1. Дополнение. Если L есть произвольный язык в алфавите X, то = \ L есть его дополнение.

2. Объединение. Если , есть произвольные языки в алфавите X, то язык L = È есть их объединение.

3. Пересечение. Если , есть произвольные языки в алфавите X, то язык L = Ç есть их пересечение.

4. Отражение. Если L есть произвольный язык в алфавите X, то язык , полученный из слов языка L путем записи его слов в обратном порядке, называется отражением языка L.

5. Конкатенация. Если , есть произвольные языки в алфавите X, то язык L = × , полученный приписыванием к слову языка слова языка (L = {α×β, α Î ,β Î }), является конкатенацией языков , .

6. Итерация. Если L есть произвольный язык в алфавите X, то язык = L È L È L×L È L×L×L È…есть итерация языка L.

7. a - аннулирование. Если L есть произвольный язык в алфавите X, то язык, полученный из него вычеркиванием из всех слов языка L буквы a, называется a - аннулированием.

8. Проекция. Пусть U, V – произвольные алфавиты и L Í , тогда U-проекцией языка L называется язык, полученный из слов языка L вычеркиванием букв языка V.

Например, если ( , ), ( , ),… – слово языка L, то слово , ,… принадлежит U-проекции языка L.

Аналогичным образом определяется V-проекция языка L.

Теорема 3.1. Класс L(A, , S) конечноавтоматных языков замкнут относительно операций 1–8.