Глава 3. Анализ и синтез дискретных систем

3.1. Применение теории днф к синтезу комбинационных логических сетей (комбинационных схем)

Пусть некоторое техническое устройство имеет входы и выходы (входные и выходные полюсы). Через входные полюсы осуществляется воздействие окружающей среды на устройство, а через выходные полюсы наблюдается реакция устройства на входные воздействия и, возможно, осуществляется воздействие устройства на внешнюю среду.

Пусть сигналы, поступающие на устройство, и его наблюдаемые сигналы определенны на конечном множестве значений, в частности на множестве {0, 1}. Поступление сигналов и их наблюдение выполняются в определенные моменты времени. Поведение устройства вне этих моментов времени не рассматривается. Такие устройства принято называть дискретными.

Если реакция устройства в момент времени t зависит только от входного воздействия в момент времени t, то устройство называют комбинационным.

Если реакция устройства в момент времени t зависит не только от входного воздействия в момент времени t, но и от воздействий, поступавших на устройство ранее, то устройство называется последовательностным или устройством с памятью.

Сначала рассмотрим математические модели, описывающие поведение и структуру комбинационных дискретных устройств.

3.1.1. Логические элементы

Под элементом будем понимать объект, который характеризуется множеством полюсов и множеством операторов. Различают входные и выходные полюсы элемента. Операторами элемента могут быть булевы функции. Тогда, имея k входных полюсов и v выходных полюсов, элемент реализует систему из v булевых функций от k переменных. Элементу, как правило, сопоставляется некоторое техническое устройство.

Функция 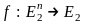, где 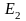= {0, 1}, называется функцией алгебры логики или булевой функцией.

Ограничимся пока рассмотрением элементов с k входными полюсами и одним выходным полюсом. Будем называть такие элементы (k, 1)-полюсниками. Каждый из них реализует одну булеву функцию. Среди (k, 1)-полюсников особую роль играют вентили, реализующие элементарные булевы функции: И, ИЛИ, НЕ И, НЕ ИЛИ, НЕ. К вентилям в последнее время относят элемент ИСКЛЮЧАЮЩЕЕ ИЛИ. На рис. 3.1 приведены примеры графического представления вентилей.

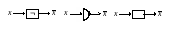
а) элемент НЕ

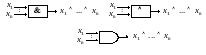
б) элемент И

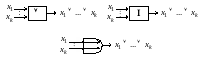
в) элемент ИЛИ

г) элемент НЕ И

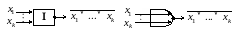
д) элемент НЕ ИЛИ

Рис. 3.1

Заметим, что сейчас, как правило, в качестве элементов дискретных устройств используются программируемые логические блоки (ПЛБ), которые реализуют произвольные булевы функции от фиксированного числа переменных. Программируются не только функции, но и связи между блоками. Программируемые блоки могут, в частности, выполнять две различные булевы функции фиксированного числа n переменных, n £ 4.

3.1.2. Комбинационные логические сети

Структура комбинационного дискретного устройства описывается логической сетью, показывающей, из каких элементов дискретное устройство состоит и как они связаны между собой.

Дадим индуктивное определение комбинационной логической сети (комбинационной схемы).

1. Всякий элемент e есть комбинационная схема. Полюсами этой схемы являются полюсы элемента e.

2. Если S – комбинационная схема, e – элемент, не содержащийся в S, то результат включения e в S, обозначенный через 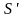, есть также комбинационная схема. Включение выполняется следующим образом. Входные полюсы элемента e отождествляются с полюсами схемы S так, что каждый полюс элемента e отождествляется не более чем с одним полюсом схемы S. Полюсами схемы являются полюсы схемы S, выходные полюсы элемента e и те входные полюсы этого элемента, которые не отождествлены с полюсами схемы S.

3. Других комбинационных схем нет.

На рис. 3.2 представлены схема S, элемент e и схема .

Комбинационная схема представляется ориентированным графом, в котором выделены вершины, называемые полюсами. Это значит, что комбинационная схема представляется ориентированной сетью. Вершины, не являющиеся полюсами (внутренние вершины сети), сопоставлены логическим элементам – отсюда название “логическая сеть”. В дальнейшем термины “комбинационная схема” и “комбинационная логическая сеть” будем использовать как синонимы. Из определения комбинационной схемы вытекают ее следующие свойства:

1. В комбинационной схеме отсутствуют ориентированные циклы.

2. Элементы схемы можно пронумеровать таким образом, что выход элемента с номером i не может быть отождествлен с входом элемента с номером j, если j < i.

Покажем, что комбинационная схема реализует систему булевых функций.

Пусть схема имеет n входных полюсов и m выходных полюсов. Сопоставим входным полюсам переменные ,…, .

Каждому полюсу схемы припишем булеву функцию следующим образом:

1. Если вершина сети есть входной ее полюс, то вершине приписывается тождественная функция , где i – номер полюса.

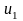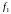2. Если вершина сети сопоставлена элементу e, реализующему функцию h( ,…, ), и вершинам ,…, приписаны функции ( ,…, ),…, ( ,…, ) от входных переменных сети, то элементу e приписывается функция h( ( ,…, ),…, ( ,…, )) от входных переменных сети.

3. Выполняя шаг 2, дойдем до элемента, выход которого является выходом схемы, приписав ему функцию от переменных ,…, .

Итак, система булевых функций описывает поведение комбинационного дискретного устройства. Система булевых функций извлекается из комбинационной схемы.

Комбинационная схема и система булевых функций являются математическими моделями, описывающими соответственно структуру и поведение дискретных устройств.

Выделяют задачи анализа и синтеза комбинационных схем.