4. Абсолютная величина вещественного числа

Абсолютной величиной (или модулем) числа х называется само число х, если x  0, или число - х, если х < 0. Абсолютная величина числа х обозначается символом | х |. Например, |+ 5| = 5; |- 5| = - (- 5) = 5; | 0 |= 0.

Основные свойства абсолютных величин:

1) | x |  0; 2) | x | = |- x |; 3) - | x | ≤ x ≤ | x |;

4) Неравенство | x | ≤ ( > 0) означает, что - ≤ x ≤ ;

5) Неравенство | x |   ( > 0) означает, что либо х  , либо х ≤ -;

6) | x ± y | ≤ | x | + | y |; 7) | x ± y |  | x | - | y |; 8) | x  y | = | x |  | y |;

9) | | = ( y  0 ).

Примеры с решениями

Пример 1. Доказать, что множество X= {1, } ограничено. Установить, какие числа являются его гранями. Найти точные верхнюю и нижнюю грани этого множества.

Решение. При любом натуральном n выполняются неравенства 0<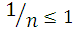 , поэтому множество X ограничено.

Докажем, что число 1 является точной верхней гранью множества X, т.е. что sup X =1. Для этого, согласно свойству точной верхней грани, надо показать, что для любого существует n такое, что выполняется неравенство .

Очевидно, что при n=1 выполняется , а это и доказывает утверждение - sup X =1.

Докажем теперь, что число 0 является точной нижней гранью множества X. Для этого надо проверить, что для любого существует n такое, что выполняется неравенство

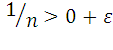. (1)

Действительно, решая неравенство (1), получаем 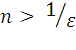. Взяв какое-нибудь натуральное число , получим требуемое n, а это, согласно определению точной нижней грани, и означает, что inf X =0.

Отметим, что данному множеству X точная верхняя грань 1 принадлежит и является его наибольшим числом, а точная нижняя грань 0 не принадлежит множеству X, и в этом множестве нет наименьшего числа.

Пример 2. Найти решения уравнений: 1). | x | = х + 2; 2). | x |= х - 2; 3). х + 2| x | = 3.

Решение. 1). При х  0 х = х + 2, откуда вытекает, что 0 = 2, т.е. рассмотренное уравнение не имеет решений.

При х < 0 получаем, что - х = х + 2, откуда следует, что х = -1 является единственным решением нашего уравнения.

2). При х  0 имеем х = х – 2 (т.е. 0 = - 2) и, следовательно, уравнение не имеет решений.

Если же х < 0 получаем, что – х = х - 2, откуда вытекает, что х = 1 > 0, что противоречит сделанному предположению (х < 0).

Таким образом, уравнение 2) не имеет решений.

3). При х  0 имеем х + 2х = 3, откуда х₁ = 1.

При х < 0 получаем х – 2х = 3, откуда х₂ = - 3.

Следовательно, х ₁ = 1 и х ₂ = - 3 есть решения уравнения.

Пример 3. Решить уравнение | х - 5| = х - 5.

Решение. По определению, | х | = х при х  0. Следовательно, данное уравнение представится в виде х – 5  0, откуда х  5.

Пример 4. Решить неравенство | 2 х – 1 | > 2 х - 1.

Решение. Так как | х |> х только при х < 0, то неравенство справедливо для тех х, при которых 2 х – 1 < 0, откуда х < .

Пример 5. Решить неравенство | х – 3 |  2.

Решение. В силу основных свойств модуля числа, х – 3  2 или х –3 ≤ - 2, откуда получаем ответ: либо х  5, либо х ≤ 1, т.е. множество всех решений рассматриваемого неравенства есть

Задачи для самостоятельного решения

Задача 1. Найти sup X и inf X ,если

1). X = { x_n : x_n = }; 2). X = { x_n : x_n =1 + };

3). X={ x_n : x_n = + + +…+ }.

Задача 2. Приведите примеры числовых множеств X, у которых:

a) sup X  X; б) sup X  X; в) inf Х  Х; г) inf Х  Х.

Задача 3. Приведите пример числового множества X, когда inf X = sup X.

Задача 4. Приведите пример числового множества X, когда inf Х  Х, a sup X  X.

Задача 5. Доказать, что множество Х = {... - 3, - 2, - 1, 0, 1, 2, 3...} всех целых чисел не ограничено ни снизу, ни сверху. В этом случае принято писать, что sup X = +  , а inf X = - .

Задача 6. Доказать, что, каковы бы ни были числа а и b, 0 < а < b, существует такое целое число n > 0, что а n > b.

Задача 7. Пусть X и Y — два непустых множества действительных чисел. Доказать, что если Y  X, то: a) sup Y ≤ sup X; б) inf Y  inf X.

Задача 8. Пусть X и Y — два непустых множества чисел, а X+Y – множество всевозможных чисел вида x + y; где x  X, y  Y. Показать, что sup ( X + Y ) = sup X + sup Y; inf (X + Y) = inf X + inf Y.

Задача 9. Пусть X и Y — два непустых числовых множества неотрицательных действительных чисел, а XY – множество всевозможных чисел вида xy; где x  X, y  Y. Показать, что sup (XY) = (sup X)(sup Y); inf (X·Y) = (inf X)(inf Y).

Задача 10. Пусть X — множество действительных чисел, а -X – множество всевозможных чисел вида y = - x; где x  X. Показать, что inf (-X)= - sup X, sup (-X)= - inf X.

Задача 11. Пусть X и Y — два непустых множества неотрицательных действительных чисел, а X-Y – множество всевозможных чисел вида x - y; где x  X, y  Y. Показать, что sup (X - Y) = (sup X) – (inf Y).

Задача 12. Решить уравнения и неравенства:

а) | x | = x + 1; б) | x | < x + 1; в) | x - 2| < 3; г) | x - 1|  2.

Задача 13. Решить уравнения и неравенства:

а) | x ² - 5 x + 1| = - (x ² - 5 x + 1); б) | x ² -5 x + 6| > x ² -5 x + 6; в) | | > ; г) | | = .

Задача 14. Решить уравнения и неравенства:

а) |x + 4| = |x – 4 |; б) | x - 1| + |1 - 2 x| = 2| x |; в) | x - 3| + | x + 3| > 8; г) | x + 3| - | x + 1| ≤ 2.

Задача 15. Решить уравнения:

а) | sin x | - sin x =2; б) x ² – 2| x | + 3= 0.

Задача 16. Решить уравнения и неравенства:

а) ||2 - 3 x | - 1| > 2; б) || x | - 2| ≤ 1; в) || x - 1| + 2| = 1;

г) || x + 1| - 2| = 2.

Задача17. Решить уравнения и неравенства:

а) |( x ² + 2 x + 5) + (x - 5)| = | x ² + 2 x + 5| + | x - 5|;

б) |( x ⁴ - 4 x) - ( x ² + 2)| = | x ⁴ - 4 x | - | x ² + 2|;

в) | x ² - 3 x | > | x ²| - |3 x |.

Задача 18. Решить неравенства:

а) | x ² - 3 x - 3 | > | x ² + 7 x - 13|; б) | x ² - 2 x - 3| < 3 x - 3.

Задача 19. Решить уравнения и неравенства:

а) | x | - 2| x + 1| + 3| x + 2| = 0; б) | x - 1| - | x | + |2 x + 3| > 3 x - 3;

в) x ² - |3 x + 2| + x = 0; г) x ² + 2| x + 3| - 10 ≤ 0.