Свойства действительных чисел
Операция сложения.
Для любых двух чисел a и b определено единственным способом число, называемое их суммой и обозначаемое a + b. Сумма обладает свойствами:
Для любых двух чисел a и b выполняется a + b= b + a. Это свойство называется переместительным (коммутативным) законом сложения.
Для любых трех чисел a, b, с выполняется a + (b + с)= (b + с)+а. Это свойство называется сочетательным (ассоциативным) законом сложения.
Существует число 0, называемое нулем, такое, что для любого числа a выполняется a + 0= a.
Для любого числа a существует число, обозначаемое -a и называемое противоположным данному, такое, что a +(- a)=0.
Далее вместо a +(- b) будем писать a - b.
Операция умножения.
Для
любых двух чисел a
и b
определено единственным способом
число, называемое их произведением
и обозначаемое a
b.
Произведение обладает свойствами:
Для любых двух чисел a и b выполняется a b= b a. Это свойство называется переместительным (коммутативным) законом умножения.
Для любых трех чисел a, b, с выполняется a
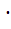(b
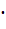с)=
(b
с)
а.
Это свойство называется сочетательным
(ассоциативным) законом умножения.Существует число 1, называемое единицей, такое, что для любого числа a выполняется a 1= a.
Для любого a
0
существует число, обозначаемое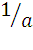 
и называемое обратным данному, такое,
что a
=1.
Связь операции сложения и умножения.
Для любых трех чисел a, b, с выполняется a (b + с)= b а + с а. Это свойство называется распределительным (дистрибутивным) законом умножения относительно сложения.
Упорядоченность.
Для любых двух чисел a и b определено одно из соотношений a < b (a меньше b), a = b (a равно b), a > b (a больше b) так, что выполняются свойства:
Если a > b , то для любого с выполняется a + c > b + c.
Если a > b, то для любого с > 0 выполняется a c > b c.
Свойство непрерывности.
Каковы бы ни были непустые множества
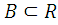у которых для любых элементов a
A,
b
B
выполняется неравенство a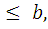
то существует такое число
z,
что для всех x
A,
y
B
выполняется
x
.
Числовые промежутки
Отрезок, интервал, полуинтервал записываются соответственно как
[a,b]={x
: a 
x
b},
(a,b)={x
: a 
x
b},
[a,b)={x : a x < b}, (a,b]={x : a x b}.
Бесконечные промежутки записываются:
(a,
+∞)={x
:x
> a},
(-∞,a)
= {x
:x
< a},
(-∞,+∞)={x
:x
R}.
Интервал
(а
– 
а
),
где 
,
называют 
- окрестностью точки а
и обозначают
(а).
Точные грани числовых множеств
Множество
X
действительных чисел (
)
называется ограниченным сверху, если
существует число c
такое, что все элементы множества X
не превосходят c,
т.е.
Множество
называется ограниченным снизу, если
существует число d
такое, что все элементы множества X
не меньше d,
т.е.
Множество
называется ограниченным, если оно
ограничено как сверху, так и снизу, т.е.
Последнее условие равносильно условию
Если
множество 
ограничено сверху, то наименьшее из
чисел, ограничивающее его сверху,
называют его точной верхней гранью или
супремумом (supremum).
Число a является точной верхней гранью множества , если выполняются следующие условия:
1)
а;
2)
a
–
.
Точная верхняя грань множества обозначается sup X.
Если множество ограничено снизу, то наибольшее из чисел, ограничивающее его снизу, называют его точной нижней гранью или инфинумом (infinum).
Число b является точной нижней гранью множества , если выполняются следующие условия:
1)
b;
2)
b
+
.
Точная нижняя грань множества обозначается inf X.
Всякое ограниченное сверху (снизу) непустое множество действительных чисел имеет точную верхнюю (нижнюю) грань.
Если множество не ограничено сверху (снизу sup X = +∞), то пишут (соответственно inf X =- ∞).