8. Похідні вищих порядків

До цього часу ми розглядали похідну від функції ,яку називають похідною першого порядку. Але похідна сама є функцією, яка може мати похідну.

Означення. Похідною n-го порядку називається похідна від похідної (n-1)-го порядку.

Позначення похідних: – другого порядку (або друга похідна), – третього порядку (або третя похідна).

Для позначення похідних вищих порядків використовуються арабські цифри і дужки або римські цифри, наприклад, або і т.д.

Приклад. Знайти перші три похідні від функції

Розв’язання. .

4.7. Диференціал функції і наближені обчислення

Згідно з означенням похідної функції маємо

.

З другого боку, змінна величина відрізняється від своєї границі на нескінченно малу , тому

. (8)

У формулі (8) доданок є нескінченно малою величиною вищого порядку, ніж .

З цього випливає, що при перший доданок у формулі (8) є головною частиною приросту функції. Він є лінійним відносно .

Означення. Головну лінійну частину приросту функції називають диференціалом цієї функції. Диференціал функції позначають через або .

Таким чином

.

Якщо взяти , тоді , а отже . Тому можемо записати формулу для обчислення диференціала у вигляді

.

З останньої рівності одержуємо, що , тобто похідну від функції можна трактувати як відношення диференціалу функції до диференціалу незалежної змінної.

Так як при , та із формули (8) випливає, що похибка у наближеній рівності

(9)

дорівнює і є нескінченно малою більш високого порядку ніж , коли

Рівність (9) часто використовується у наближених обчисленнях.

Якщо , то і рівність (9) набуває вигляду

.

Приклад 1. Нехай . Оскільки , то при достатньо малих х маємо .

Аналогічно можна показати, що при достатньо малих х мають місце наближені рівності , , , .

Приклад 2. Нехай r – ставка банківського відсотку (за рік). Знайдемо кількість років n, на протязі яких початкова сума внеску збільшиться у два рази. Оскільки за n років внесок збільшиться в раз, то фактично нам потрібно розв’язати рівняння .

Логарифмуючи це рівняння, одержимо . Звідки .

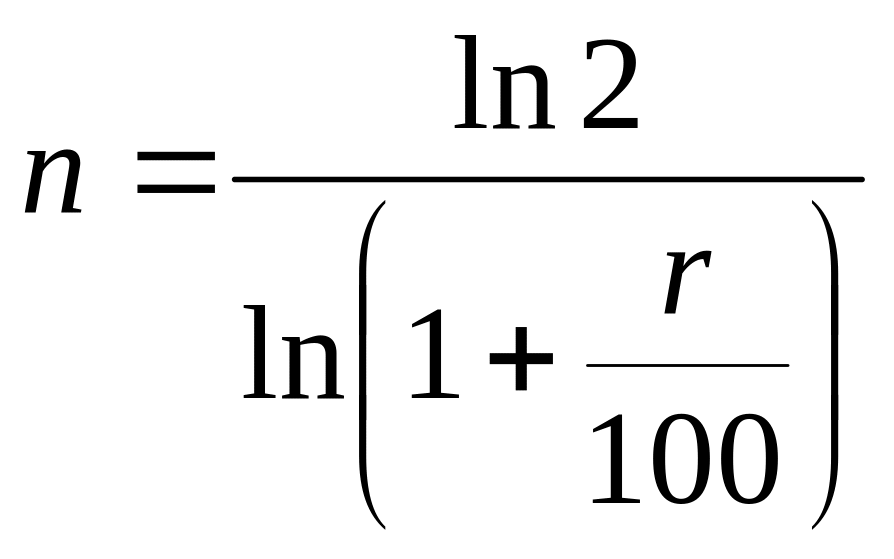Замінюючи логарифм у знаменнику його наближеним значенням, одержимо . Так як , то час подвоєння внеску буде (правило сімдесят).

Якщо, наприклад, відсоткова ставка – 10%, то час подвоєння внеску буде приблизно 7 років. А більш точне значення роки.

4.8. Логарифмічна похідна

Означення. Логарифмічною похідною додатної функції називається похідна . Оскільки , то згідно правила диференціювання складної функції одержимо наступне співвідношення для логарифмічної похідної: .

Якщо похідну розглядати як швидкість зміни функції у, то величину природно вважати її відносною швидкістю зміни або її темпом росту.

Застосування логарифмічної похідної. Нехай – наближена величина внеску в момент часу t. Чи можна визначити (наближено) ставку банківського відсотку r за допомогою функції К(t)? Якщо відсотки нараховуються один раз за період часу ∆t, то відсотки за вказаний період будуть дорівнювати (ми вважаємо, що r номінальна ставка за рік, ∆t – частка року). Оскільки приріст внеску і відсотки від внеску – теж саме, то . Звідси

.

Нехай функція має похідну . Тоді приріст функції можемо (наближено) замінити на диференціал , в результаті чого одержимо

.

Висновок: ставка банківського відсотка r співпадає з логарифмічною похідною від величини внеску.

Приклад. Нехай , де t – число років від відкриття внеску, К₀ – величина внеску в початковий момент часу t=0. Тоді ми можемо визначити, як змінювалась ставка відсотку . Дійсно

або у відсотках .

Так, через два роки після відкриття внеску ставка була річних, через 5 років ставка зменшилась до 25% річних і т.д. Відмітимо, що абсолютна швидкість росту внеску при цьому не спадала, а зростала, оскільки .

Завдання для самостійної роботи

1. Знайти похідні першого порядку заданих функцій:

,	,	,
,	,	,
,	,	,
,	,	,
,	,	,
,	,	,
,	,	,
,	,	,
,	,

2. Знайти похідні першого порядку функцій, заданих неявно та параметрично:

, , , , , ,

, , , , , , .

3. Який кут утворює з віссю абсцис дотична парабола , яка проведена в точці М(2;3)? Записати рівняння цієї дотичної.

4. Скласти рівняння дотичної і нормалі до кривої в точці М(1;-1)

5. Скласти рівняння дотичної до гіперболи , проведеної в точці М(-9;-8).

6. Знайти похідні другого порядку:

а) , б) , в) , г) , д) ,

е) , ж) , з) .

7. Знайти похідні третього порядку: а) , б) .

8. Обчислити наближені значення:

а) , б) , в) , г) .

12