
- •Краткое описание метода конечных элементов для линейных задач.
- •Общие положения
- •Библиотека конечных элементов для линейных задач.
- •Универсальный стержень (кэ 10)
- •Универсальные конечные элементы балок-стенок, тонких плит и пологих оболочек (типы кэ 11, 12, 21-24,27, 30, 41, 42, 44)
- •Универсальные конечные элементы пространственной задачи теории упругости (кэ 31-34,36)
- •Специальные конечные элементы (кэ 51, 53,54,55)
- •Решение системы канонических уравнений
- •Расчет на динамические воздействия
- •2. Для сейсмической нагрузки
- •3. Для импульсивной и ударной нагрузок
- •4. Для гармонической нагрузки вычисляются суммарные по всем формам инерционные силы s1 и s2 , соответствующие косинусоидальной (действительной) и синусоидальной (мнимой) составляющим:
- •Суперэлементное моделирование
- •Принципы определения расчетных сочетаний усилий (рсу)
- •Стержни
- •Плоское напряженное состояние
- •Оболочки
- •Объемные элементы
- •Загружения
- •Расчет на устойчивость
- •Решение нелинейных задач
- •Общие положения
- •Расчет физически нелинейных задач
- •Библиотека законов деформирования материалов
- •Типы дробления сечений стержней
- •Типы арматурных включений
- •Библиотека конечных элементов для физически нелинейных задач
- •Стержневые конечные элементы (кэ 210 и 205)
- •Конечные элементы тонких пластин и пологих оболочек (кэ 221-224, 227, 230, 241, 242, 244)
- •Конечные элементы плоской деформации грунтов (кэ 281, 282, 284)
- •Конечные элементы для решения пространственной задачи теории упругости (кэ 231-234, 236)
- •Библиотека конечных элементов для геометрически нелинейных задач
- •Универсальный стержневой элемент (кэ - 310)
- •Конечный элемент предварительного натяжения (кэ 308)
- •Конечные элементы тонких пологих оболочек (кэ 341, 342, 344)
- •Специальные конечные элементы односторонних связей
- •Одноузловой элемент односторонней связи (тип кэ-261)
- •Двухузловой элемент одностоpонней связи (тип кэ - 262)
- •Специализированный процессор монтаж для расчета сооружений в стадии возведения
- •Замечания по составлению расчетных схем и некоторые пояснения.
- •Принципы построения конечно-элементных моделей
- •Рациональная разбивка на конечные элементы
- •Глобальная, местная и локальная системы координат
- •Объединение перемещений
- •Абсолютно жесткие вставки
- •Угол чистого вращения
- •Моделирование податливости узлов сопряжения элементов
- •Моделирование шарниров в стержневых и плоскостных элементах
- •Расчет на заданные перемещения
- •Введение связей конечной жесткости
- •Расчет на температурные воздействия
- •Моделирование предварительного напряжения
- •Учёт прямой и косой симметрии
- •Вычисление коэффициентов постели упругого основания
- •Учет работы конструкций совместно с упругим основанием
- •Расчет оболочек и плит, подкреплённых рёбрами
- •Задание весов масс и динамических воздействий
- •Сбор нагрузок на фундаменты
- •Расчетные сочетания нагрузок
- •Согласованная система координат для пластин
- •Принципы анализа результатов расчета
- •Правила знаков при чтении результатов расчета.
- •Результаты расчета на динамические воздействия
- •Суммарные усилия от динамических воздействий
- •Документирование
- •Жесткостные характеристики элементов
- •Проверка прочности по различным теориям
- •Главные напряжения
- •Кэ плоской задачи теории упругости
- •Кэ плиты
- •Кэ объемного ндс
- •Кэ оболочки
- •Стержневые кэ
- •Вычисление эквивалентных напряжений
- •Результаты расчета
- •Расчет и проектирование стальных конструкций
- •Назначение и возможности
- •Проектируемые сечения
- •Задание дополнительных данных для расчета
- •Конструктивные и унифицированные элементы
- •Проверки несущей способности элементов
- •Описание алгоритмов
- •Сквозной расчет
- •Локальный расчет
- •Представление результатов расчета
- •Подбор и проверка армирования в железобетонных элементах
- •Армирование стержневых элементов
- •Проверка заданного армирования
- •Армирование пластинчатых элементов
Результаты расчета на динамические воздействия
При расчете на сейсмические, ветровые с учетом пульсации, ударные и импульсивные воздействия определяются собственные частоты i(i<KF), где KF - количество форм, заданное пользователем. Вычисляются также периоды собственных колебаний Ti , формы колебаний, инерционные силы и соответствующие им перемещения и усилия. При этом каждая форма порождает единственную составляющую инерционных сил.
При расчете на гармонические колебания каждая i-тая форма колебаний порождает пару инерционных сил - вещественную составляющую и мнимую составляющую. Эта пара составляющих и называется i-тым вариантом. Составляющие инерционных сил варианта не имеют физического толкования, но их использование в качестве статических загружений позволяет определить амплитудные значения перемещений, усилий и напряжений для этого варианта.
Количество вычисляемых вариантов и количество учитываемых форм - это не одно и то же. 1-ая форма колебаний порождает 1-ю и 2-ю составляющие, которые образуют 1-й вариант. 2-ая форма колебаний порождает 3-ю и 4-ю составляющие, которые образуют 2-ой вариант, и т.д.
При расчете на гармонические колебания без учета частотных зон (модуль 24) по умолчанию производится учет резонансных состояний для частот i, предшествующих заданной вынужденной частоте . Пусть К количество форм собственных колебаний, для которых частоты i<, где -заданная частота вынужденных колебаний. Если К<(kf/2) ( где – целая часть, kf – заданное количество форм колебаний), то К=(kf/2), и тогда рассматривается всего К вариантов данного загружения. Из них (К-1) вариант соответствует вынужденным частотам i=i (i<К), а К-тый вариант соответствует заданной вынужденной частоте .
В противном случае рассматривается (К+1) вариантов. Из них К вариантов соответствует вынужденным частотам i=i (iК), а (К+1)-ый вариант соответствует заданной вынужденной частоте .
От учета предшествующих частот при задании исходных данных можно отказаться.
При расчете на гармонические колебания с учетом частотных зон (модуль 28) принимаются во внимание как возможная погрешность в определении собственных частот, так и возможное изменение собственных частот конструкций в процессе их эксплуатации. При введении так называемых частотных зон предполагается, что внутри них должно находиться расчетное значение собственной частоты. Границы частотных зон определяются по формулам:
![]() ;
; ![]() ; (10.1)
; (10.1)
где
![]() ,
,
![]() -левая и правая границы частотной зоны;
-левая и правая границы частотной зоны;
![]() - погрешность в определения частоты,
заданная в зависимости от типа конструкций
и расчетной схемы;
- погрешность в определения частоты,
заданная в зависимости от типа конструкций
и расчетной схемы;
![]() - 1-я частота собственных колебаний,
определенная в результате расчета.
- 1-я частота собственных колебаний,
определенная в результате расчета.
При расчете на гармонические колебания с помощью модуля 28 предполагается, что частоты собственных колебаний конструкции могут иметь любое значение в пределах расширенных частотных зон, полученных с учетом возможной погрешности в определении частот. Поэтому при гармонической нагрузке частоты собственных колебаний определяются следующим образом:
если вынужденная частота попадает в К-ю частотную зону (рис. 10.1.а) то
![]() при
при
![]() ,
,
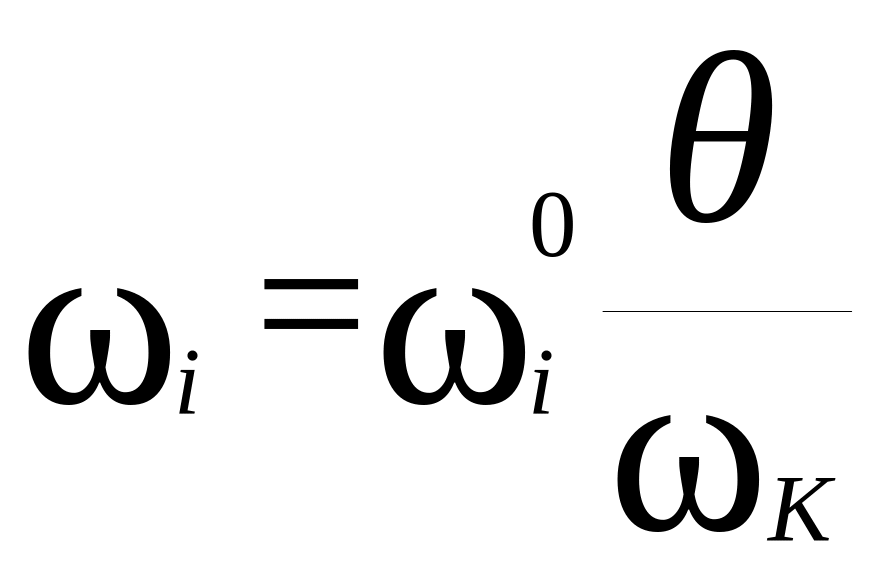 при
при
![]() ,
то есть собственная
,
то есть собственная
частота К-й частотной зоны принимается равной вынужденной частоте, а остальные частоты принимаются пропорционально. Если вынужденная частота попадает в межчастотную зону (рис. 10.1.б), то собственные частоты принимаются равными сначала левым границам частотных зон, а затем - правым.
а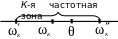 )
)
б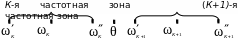 )
)

Рис. 10.1 Определение частот собственных колебаний.
а) - при попадании вынужденной частоты в частотную зону,
б) - при попадании вынужденной частоты в межчастотную зону.
При разложении гармонической нагрузки по формам собственных колебаний учитывается следующее количество частот: три первых частоты, а затем четыре, которые лежат в области возмущающей нагрузки - по две частоты, находящиеся справа и слева.
Если величина вынужденной частоты меньше основной или больше самой высокой частоты, то в расчете учитываются три первых или три первых и две последних частоты.
На основании введения частотных зон учитывается возможное количество вариантов инерционных сил при попадании частоты возмущающей силы в частотные и межчастотные зоны. В первом случае количество вариантов инерционных сил соответствует количеству попаданий частоты возмущающей силы в частотные зоны, но не более пяти. Во втором случае количество вариантов инерционных сил зависит от соотношения величины частоты возмущающей силы и частот собственных колебаний.
Если частоты силы больше максимального или меньше минимального значений частоты собственных колебаний, то количество вариантов инерционных сил равно одному. Если же частота возмущающей силы попадает в межчастотную зону, то количество вариантов инерционных сил равно двум.
Амплитудные значения вещественной и мнимой составляющих инерционных сил при действии гармонической силы (Pcost) определяются согласно формулам:
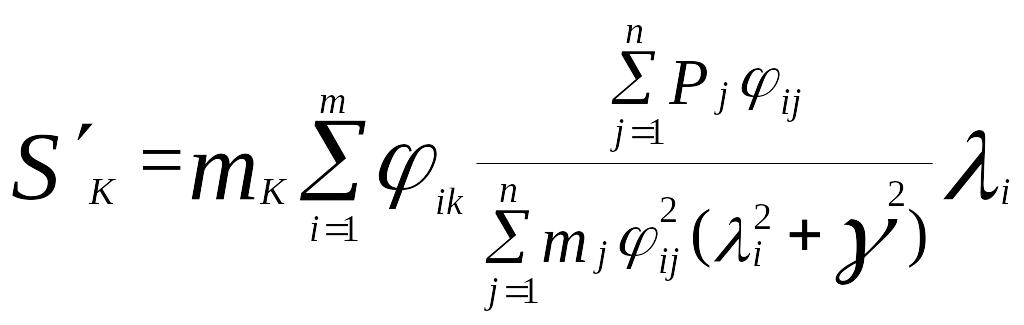 , (10.2)
, (10.2)
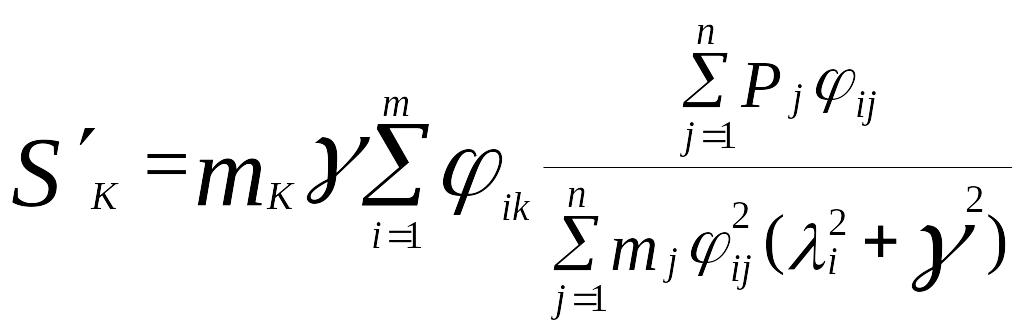 , (10.3)
, (10.3)
Здесь
Sk, Sk – соответственно вещественная и мнимая составляющие инерционной силы по направлению k–той степени свободы;
Pj – амплитуда внешнего воздействия по j–той степени свободы;
mk, mj – массы, действующие по направлению k–той и j–той степеней свободы;
ij, ik – относительные ординаты i-той формы собственных колебаний по направлению j-той и k–той степеней свободы;
i =1-2/i2, где - - частота вынужденных колебаний, i – частота i-той формы собственных колебаний;
- коэффициент неупругого сопротивления материала.
