13. Учёт прямой и косой симметрии

Если рассчитываемая схема имеет плоскости симметрии, то для уменьшения размерности задачи рекомендуется вводить в расчет часть схемы, ограниченную этими плоскостями.

На узлы, лежащие в плоскости прямой симметрии, налагаются связи, ортогональные этой плоскости, а при косой симметрии - параллельные ей. В табл.9.1 показано, по каким направлениям степеней свободы на эти узлы накладываются связи.

Таблица 9.1

	Симметрия
	прямая			косая
Плоскости симметрии или параллельные ей	XOZ	XOY	YOZ	XOZ	XOY	YOZ
Налагаемые связи	Y,UX, UZ	Z,UX, UY	X,UY, UZ	X,Z, UY	X,Y, UZ	Y,Z UX

Если плоскость симметрии не параллельна ни одной из плоскостей общей системы координат, то наложение соответствующих связей можно выполнить с помощью локальной системы координат узла.

Если имеются абсолютно жёсткие связи, не совпадающие с направлением осей общей системы координат, то они реализуются также с помощью локальной системы координат узла.

14. Вычисление коэффициентов постели упругого основания

В ПК ЛИРА реализована модель основания П.Л. Пастернака [24], которая характеризуется двумя коэффициентами постели C1 (тс/м3), C2 (тс/м), описывающими только вертикальные деформации (осадки) оснований и фундаментов. При этом параметр C2 учитывает работу грунта за пределами фундамента. В случае C2 = 0 модель Пастернака является аналогом классической модели основания Винклера.

Для одного или для двух слоев основания П.Л. Пастернак предлагает следующие формулы (даны для справки).

1. Ленточный фундамент на однослойном основании:

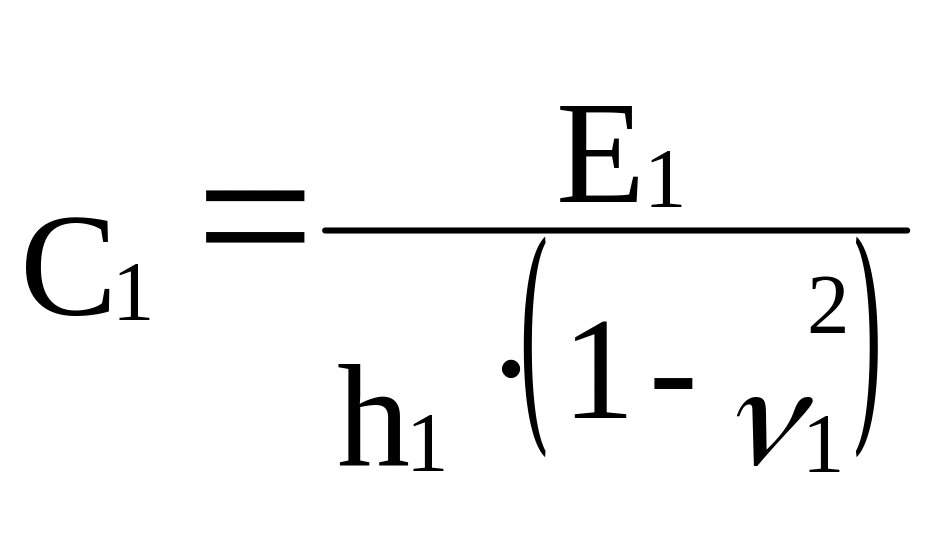(9.2)

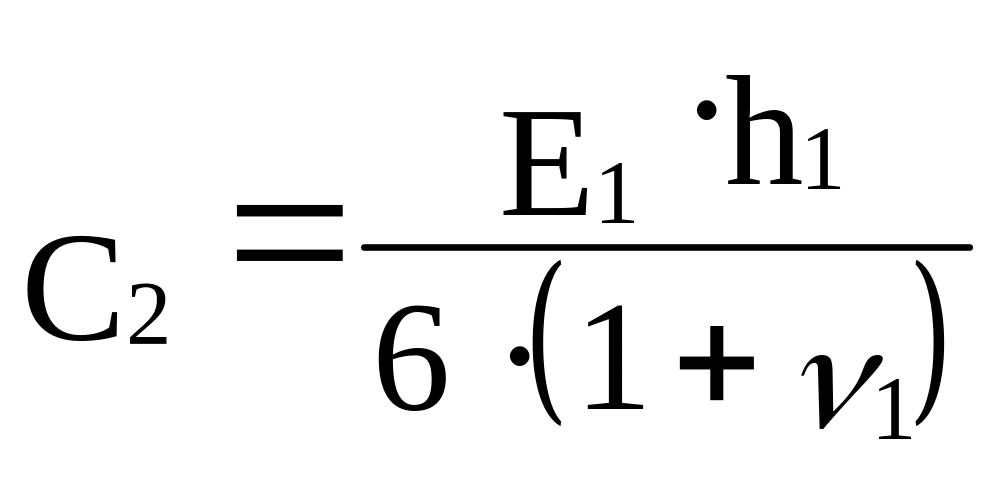(9.3)

2. Ленточный фундамент на двухслойном основании:

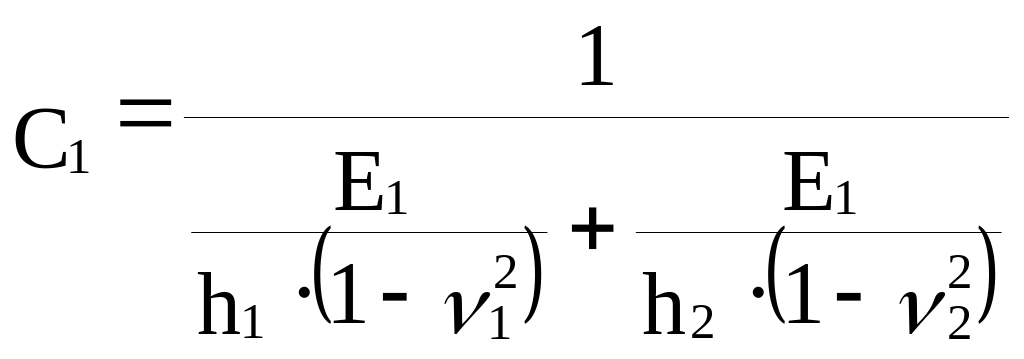(9.4)

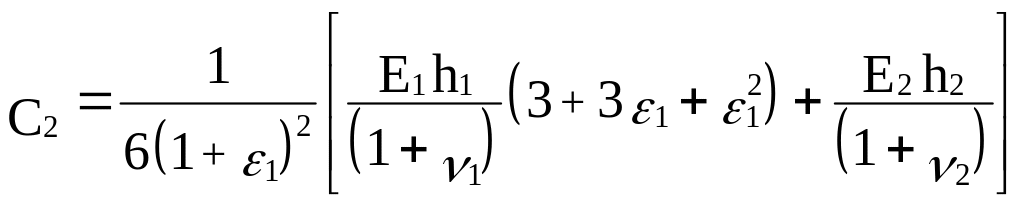(9.5)

3. Плитный фундамент на однослойном основании:

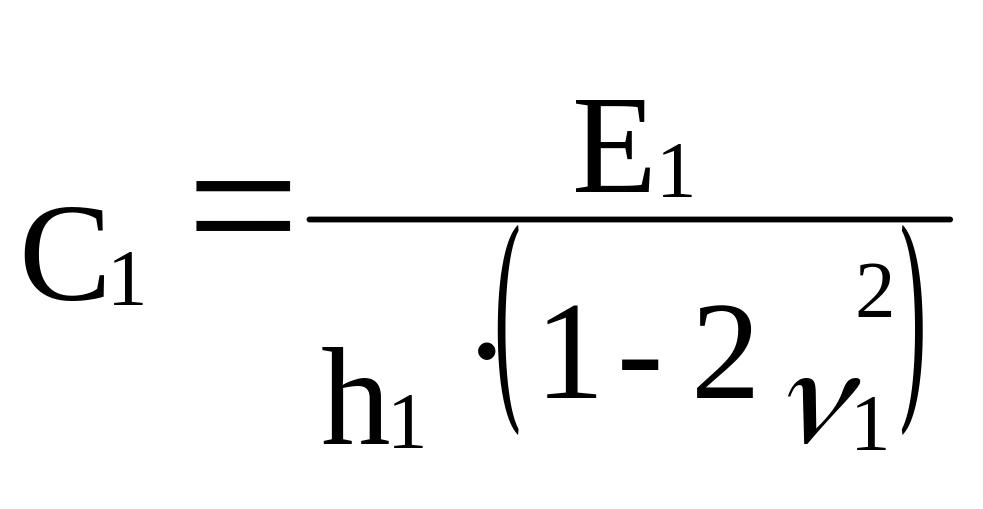(9.6)

(9.7)

4. Плитный фундамент на двухслойном основании:

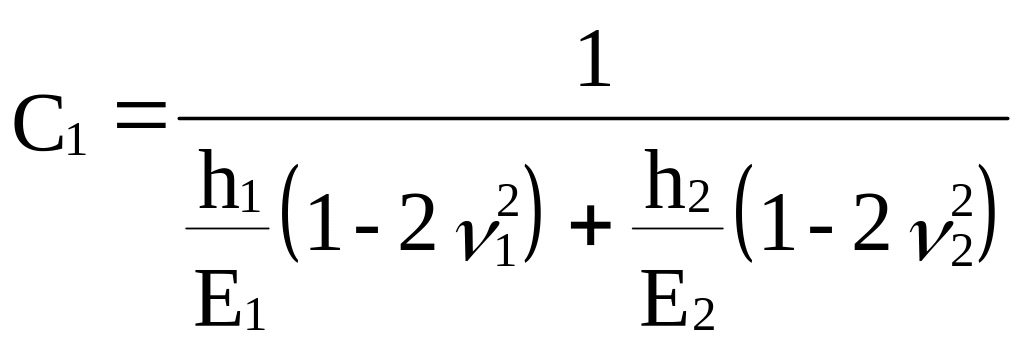(9.8)

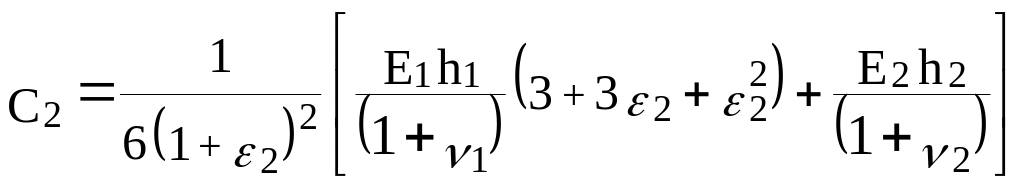(9.9)

где : E₁, v₁, h₁, E₂, v₂, h₂, - соответственно модуль деформации, коэффициент Пуассона и толщина первого и второго слоев сжимаемой толщи грунтового основания, глубина (H) которой определяется по нормам;

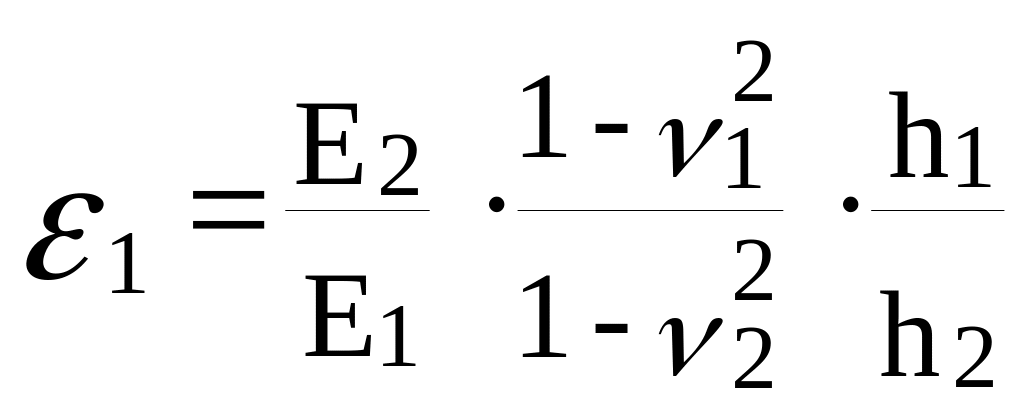(9.10)

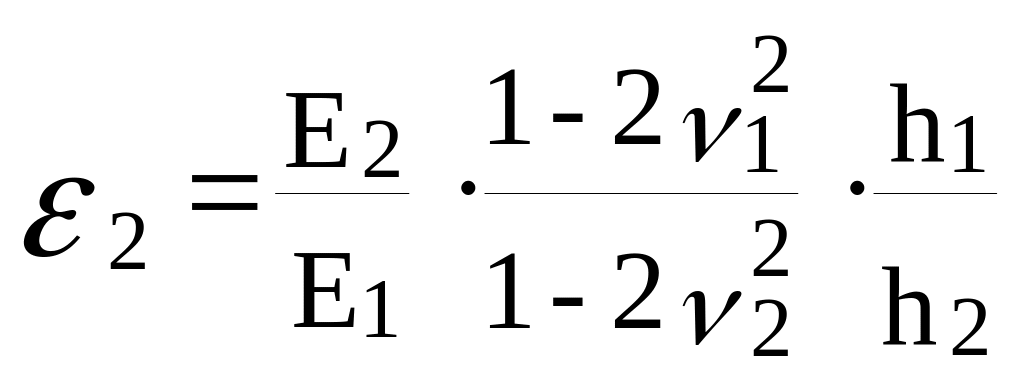(9.11)

Вычисление коэффициентов постели С1 и С2 в ПК ЛИРА производится по схеме линейно деформируемого полупространства с усредненными характеристиками многослойного основания – модулем деформации E_гр и коэффициентом Пуассона _гр:

E_гр = (z_pk*h_k)/(z_pk*h_k/E_k),

_гр= (_k*h_k)/Н_с ( k=1-> m), где

z_pk - среднее дополнительное вертикальное напряжение в подслое k (каждый слой дробится на 8 подслоев);

h_k – толщина подслоя k;

E_k – модуль деформации подслоя k;

_k – коэффициент Пуассона подслоя k;

Н_с – глубина сжимаемой толщи;

m – количество подслоев.

С1 = Е_гр/(Н_с*(1- _гр²));

С2 = Е_гр*Н_с/(6(1+ _гр)). (9.12)