Пример 1.

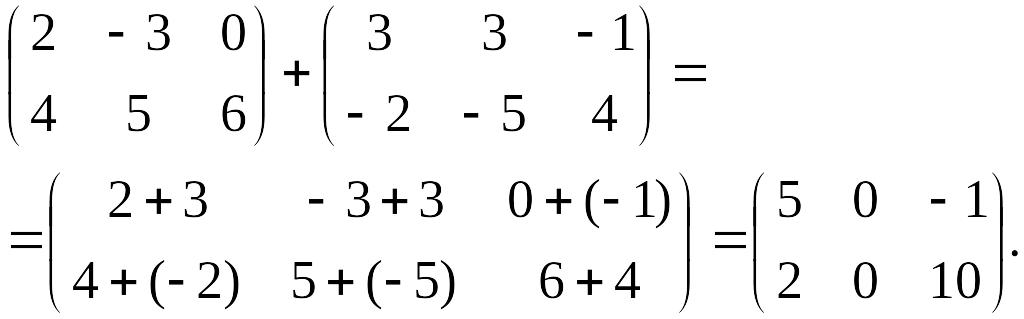
Пример 2. Найти произведение матриц и :

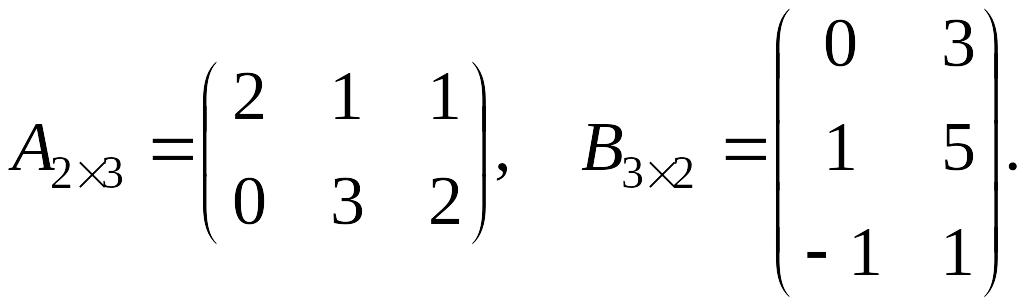
Решение:

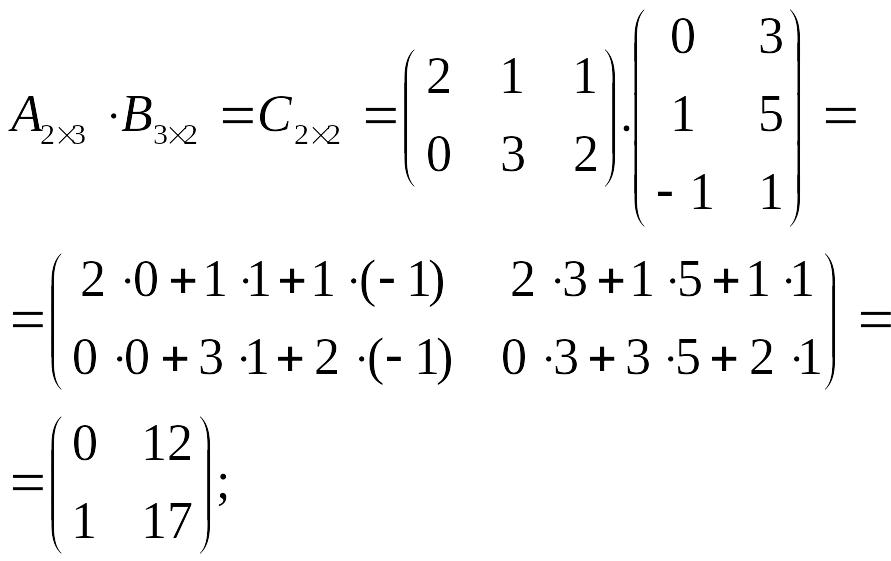
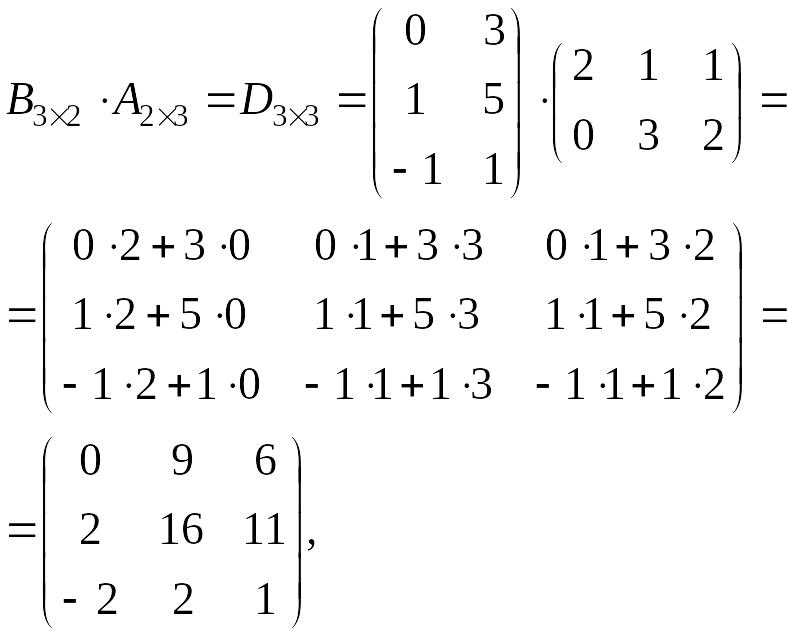
т.е. .

Пример 3. Найдём обратную матрицу:

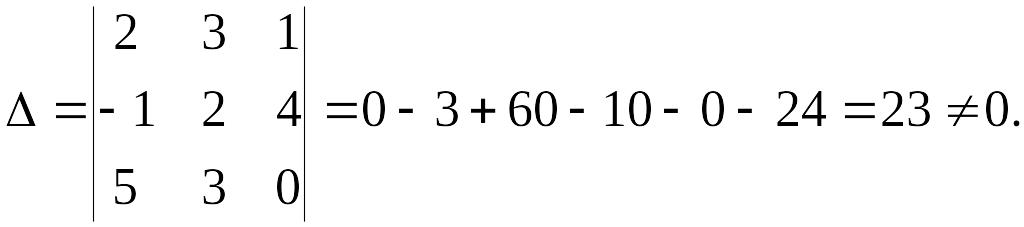
Обратная матрица имеет вид:

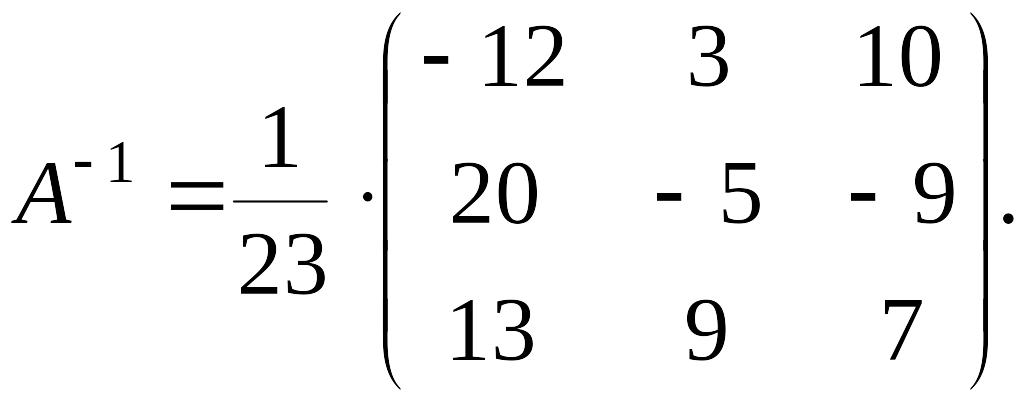
Индивидуальные задания для самостоятельного решения

Найти обратную матрицу для матрицы

9.Показать, что матрица А является обратной для матрицы В, если

10.Найти обратную матрицу для матрицы

Практическое занятие № 7 Решение систем алгебраических уравнений методом Крамера.

Цель: Обеспечить усвоение понятий: определитель, правило Крамера. Сформировать умения находить решение систем линейных алгебраических уравнений, используя правило Крамера. Развивать умения самостоятельной работы, логическое мышление, правильно формулировать свои мысли в процессе общения, систематизировать полученные знания. Воспитать познавательный интерес.

Студент должен знать:

• формулы для вычисления определителей второго и третьего порядков;

• правило Крамера.

Студент должен уметь:

• находить определитель матрицы,

• формулы Крамера.

Вопросы для самоконтроля

1. Определитель матрицы.

2. Формулы Крамера.

3. Алгоритм решения системы линейных алгебраических уравнений, используя правило Крамера.

Типовое задание

Пример 1.

Решить систему уравнений методом Крамера.

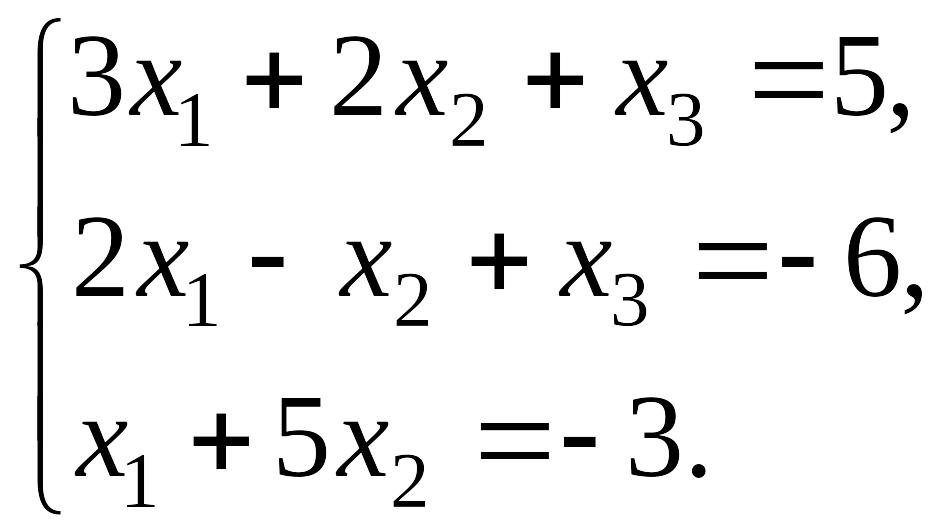
Решение:

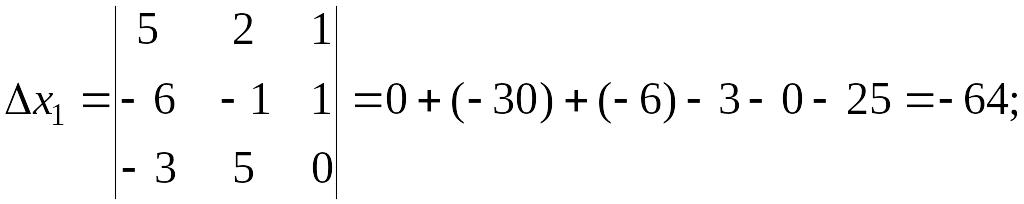
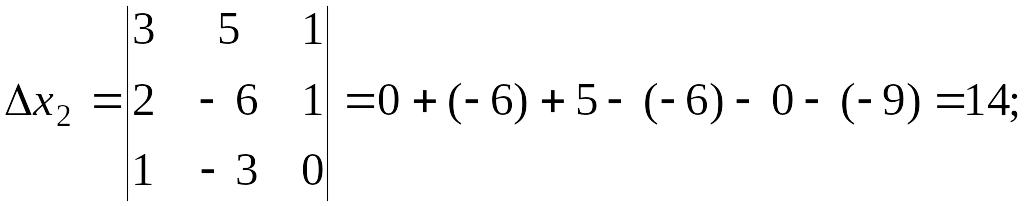
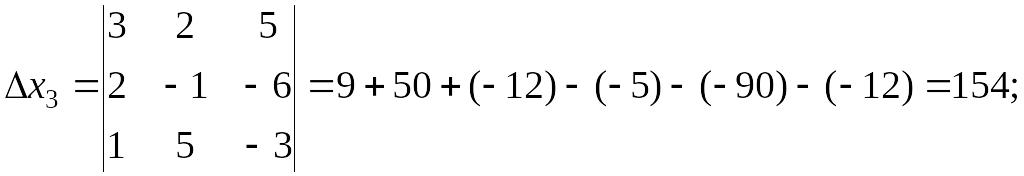
ПРОВЕРКА:

Индивидуальные задания для самостоятельного решения

Решить систему линейных уравнений методом Крамера:

1. 2. 3. 4.

5. 6) 7) 8)

9. 10.

Практическое занятие № 8 Решение простейших задач на определение вероятности с использованием теорем сложения и умножения вероятностей.

Цель: Обеспечить закрепление понятий: зависимые, независимые события, условная вероятность. Сформировать умения и навыки применять при решении задач теоремы сложения и умножения вероятностей, понятие условной вероятности.

Студент должен знать:

• понятия зависимые, независимые события, условная вероятность,

• теорему сложения вероятностей,

• теорему умножения вероятностей,

• понятие условной вероятности.

Студент должен уметь:

• решать простейшие задачи на определение вероятности с использованием теоремы сложения вероятностей.

Вопросы для самоконтроля

1. Зависимые, независимые события.

2. Условная вероятность.

3. Теорема сложения вероятностей.

4. Теорема умножения вероятностей.

Типовое задание

Пример 1. Вероятность того, что стрелок при стрельбе по мишени выбьет:

10 очков - 0,15; 9 очков - 0,2; 8 очков - 0,3; 7 очков - 0,35.

Найти вероятность того, что стрелок выбьет более 7 очков.

Решение:

= {стрелок выбьет 10 очков};

= {стрелок выбьет 9 очков};

= {стрелок выбьет 8 очков};

= {стрелок выбьет 7 очков}.

А = {стрелок выбьет более 7 очков} =

={стрелок выбьет 8 или 9 или 10 очков}

, «+» - логическое «или»

события , и несовместные события, так как в одном опыте одновременно произойти не могут.

По теореме сложения вероятностей для несовместных событий, получим:

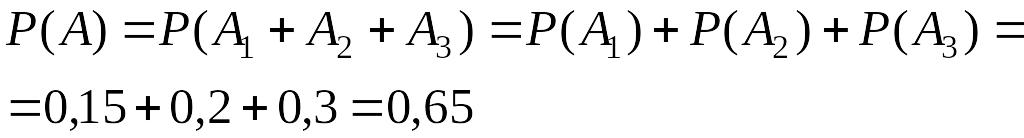
Ответ:

Вероятность того, что стрелок выбьет более 7 очков, равна 0,65.

Пример 2.

Подбрасывается игральный кубик.

Какова вероятность того, что выпадет число, кратное двум или кратное трем?

Решение:

А = {Выпадет число, кратное двум или кратное трем}

В = {выпадет число, кратное двум} = {2, 4, 6},

С = {выпадет число, кратное трем} = {3, 6}.

Логическому «или» соответствует знак «+».

А = В + С

Для того, чтобы найти вероятность события А нужно применить теорему сложения.

Далее необходимо определить события В и С являются совместными или несовместными.

Так как события В и С могут одновременно появится в одном опыте

(если выпадет 6), то события В и С – совместны.

По теореме сложения вероятностей для совместных событий

где - число исходов, благоприятствующих событию А

n – общее число исходов

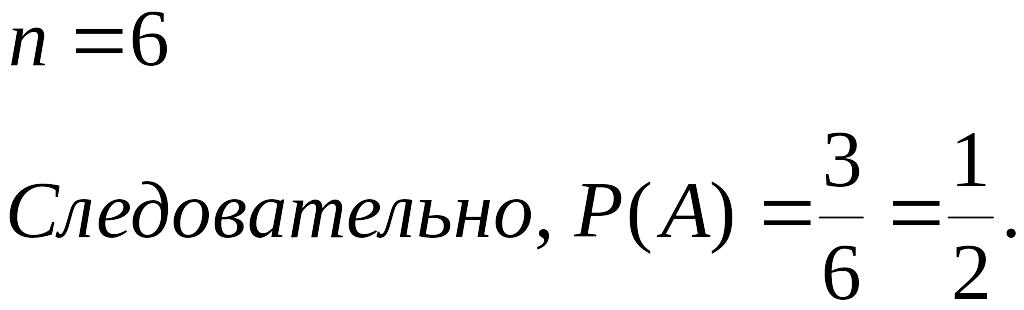
где - число исходов, благоприятствующих событию В

так как умножение событий – это событие, состоящее в их совместном появлении.

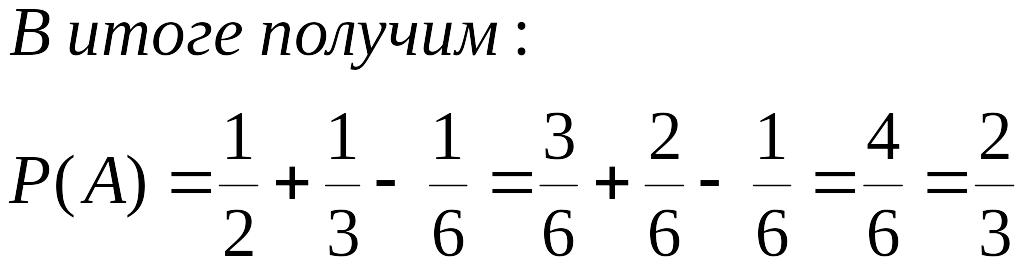
Ответ: Вероятность того, что выпадет число, кратное двум или трем, равна 2/3.

Пример 3. Студент ищет нужную формулу в трех справочниках. Вероятность того, что он найдет эту формулу в 1-ом справочнике, равна 0,9, во 2-ом – 0,7 и в 3-ем – 0,4. Найти вероятность того, что студент найдет нужную формулу хотя бы в одном справочнике.

Решение:

={студент найдет формулу в 1-ом справочнике},

={студент найдет формулу во 2-ом справочнике},

={студент найдет формулу в 3-ем справочнике},

={студент найдет нужную формулу хотя бы в одном справочнике}.

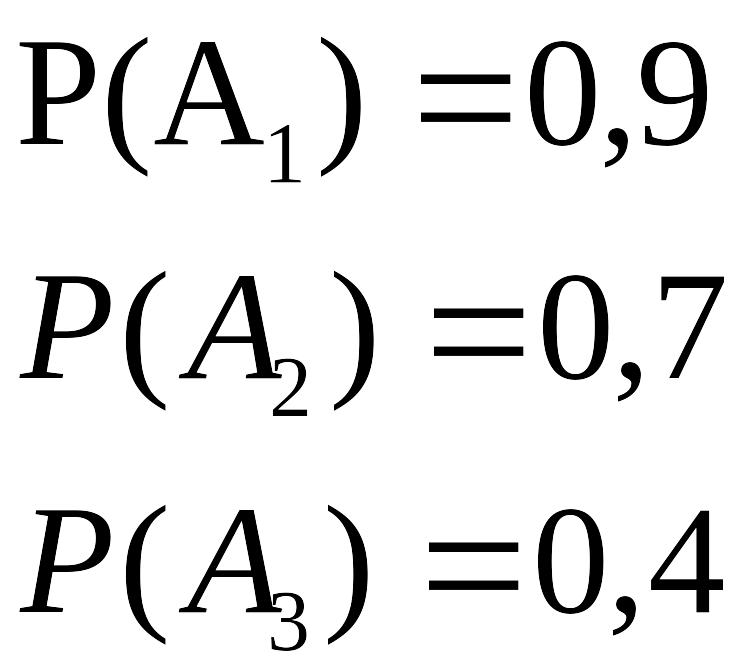
Вероятность появления хотя бы одного события находим по формуле:

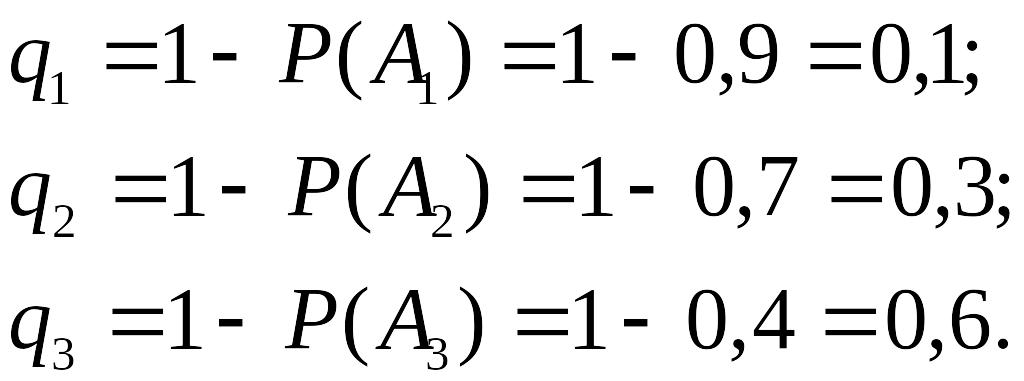
Ответ:

Вероятность того, что студент найдет нужную формулу хотя бы в одном справочнике, равна 0,982.

Индивидуальные задания для самостоятельного решения

1. На стеллаже библиотеки в случайном порядке расставлено 15 учебников, причём пять из них в переплёте. Библиотекарь берёт наудачу три учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплёте.

2. Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сработает первый сигнализатор, равна 0,95, второй – 0,8. Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.

3. Устройство состоит из трёх элементов, работающих независимо. Вероятности безотказной работы (за время t) первого, второго и третьего элементов соответственно равны 0,6; 0,7; 0,8. Найти вероятности, что за время t будут работать: а) только один элемент; б) только два элемента; в) все три элемента.

4. В читальном зале имеется 6 учебников, причём три из них в переплёте. Библиотекарь берёт наудачу два учебника. Найти вероятность того, что оба учебника окажется в переплёте.

5. Среди 100 лотерейных билетов есть 5 выигрышных. Найти вероятность того, что два наудачу выбранные билета окажутся выигрышными.

6. В цехе работают 7 мужчин и 3 женщины, по табельным номерам наудачу отобраны 3 человека. Найти вероятность того, что все отобранные лица окажутся мужчинами.

7. В ящике 10 деталей, среди которых 6 окрашенных. Сборщик наудачу извлекает 4 детали. Найти вероятность того, что все извлечённые детали окажутся окрашенными.

8. В электрическую цепь последовательно включены три элемента, работающие независимо один от другого. Вероятности отказа первого, второго и третьего элементов соответственно равны: 0,1; 0,15; 0,2. Найти вероятность того, что тока в цепи не будет.

9. Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросить четыре бомбы, вероятности попадания которых соответственно равны: 0,3; 0,4; 0,6, 0,7.

10. Вероятность хотя бы одного попадания стрелком в мишень при трёх выстрелах равна 0,875. Найти вероятность попадания при одном выстреле.

Семинарское занятие №1,2 Защита реферата, доклада, презентации.

Цель: Ознакомление с применением производной в экономике, теорией одноресурсной и многоресурсной фирмы, с комплексными числами.

Студент должен знать:

• • Понятие производной и ее применение при решении экономических задач.

  • Функциональные зависимости, используемые в экономике.

  Формулу Уилсона.

• Понятие комплексного числа и его виды.

Темы для обсуждения:

«Применение производной в экономике», «Функциональные зависимости, используемые в экономике», «Экономическая интерпретация непрерывности», «Теория одноресурсной и многоресурсной фирмы», «Формула Уилсона (работа идеального склада)», «Прибыль фирмы и объём поступления налогов при данной налоговой ставке», «Комплексные числа».

Список литературы

Основные источники:

1. Григорьев, С. Г. Учебник / С. Г. Григорьев, С. В. Задулина. – М.: Академия, 2005. – 384 с.

Дополнительные источники:

1. Григорьев, В. П. Элементы высшей математики: учебник для студентов учреждений среднего профессионального образования / В. П. Григорьев, Ю. А. Дубинский. – 4-е изд. – М.: Академия, 2008. – 320 с.

2. Партыка Т.Л. Математические методы: учебник / Т. Л. Партыка, И. И. Попов. – М.: ФОРУМ-ИНФРА-М, 2005. - 464 с.

3. Данко, П. Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч.1: Учебное пособие для вузов / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова, С. П. Данко. – 6-е изд. – М.: Оникс, 2007. – 304 с.

4. Данко, П. Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч.2: Учебное пособие для вузов / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова, С. П. Данко. – 6-е изд. – М.: Оникс, 2007. – 416 с.

Интернет-источники:

1. http://en.edu.ru - естественно-научный портал

2. http://www.bestlibrary.ru - On–line библиотека

3. http://www.km.ru/literature/ - электронная библиотека LIB.KM.ru