
- •Е.В. Сорокина дискретная МатЕматика
- •1. Множества и основные операции над ними
- •1.1. Множества, способы их задания Вопросы для повторения
- •1.2. Основные операции над множествами Вопросы для повторения
- •Тестовые задания
- •2. Основные понятия комбинаторики
- •2.1. Перестановки, размещения и сочетания Вопросы для повторения
- •2.2. Бином Ньютона Вопросы для повторения
- •Тестовые задания
- •3. Алгебра логики
- •3.1. Логика высказываний и предикатов
- •Вопросы для повторения
- •3.1.1. Определения и свойства логических операций. Сложные высказывания
- •3.1.2. Таблицы истинности
- •3.2. Булевы функции
- •Вопросы для повторения
- •3.2.1. Определения и свойства логических операций. Сложные высказывания
- •3.2.2. Минимизация булевых функций с помощью карт Карно
- •3.2.3. Анализ и синтез комбинационных устройств в заданном базисе
- •Тестовые задания
- •4. Элементы теории графов
- •4.1. Основные понятия теории графов Вопросы для повторения
- •4.2. Сетевое планирование Вопросы для повторения
- •5. Теория алгоритмов и конечные автоматы
- •5.1. Алгоритмы Вопросы для повторения
- •5.2. Построение конечных автоматов Вопросы для повторения
- •Список рекомендуемой литературы
- •Оглавление
- •Дискретная математика
Тестовые задания
Пусть Х,
Y
– произвольные множества,
![]() ;
– пустое множество.
;
– пустое множество.
1. Найти
![]() .
.
Ответы:
1.
![]() 2.
3. Х
2.
3. Х
2. Найти
![]() .
.
Ответы:
1.
![]() 2.
Y
3.
2.
Y
3.
![]()
3. Найти U\Y.
Ответы:
1.
2.
![]() 3.
3.
![]()
2. Основные понятия комбинаторики
Пусть имеется
множество, содержащее n
различных элементов. Каждое упорядоченное
подмножество состоящее из k
элементов, взятых из n
данных называется размещением
из n
элементов по k
элементов (n
k
0):
![]() .
.
Размещения из n
элементов по n элементов называются
перестановками из n элементов:
![]() .
.
Пусть имеется
множество, состоящее из n
элементов. Каждое его подмножество,
содержащее k
элементов,
называется сочетанием
из n
по k
элементов:
![]() .
.
Свойства сочетаний:
1. ![]() . 2.
. 2. ![]() .
.
Двучлен (а+b)n носит название бинома Ньютона, где а, b – произвольные числа, а n – натуральное произвольное число. Для произвольных чисел а и b и произвольного натурального числа n справедлива формула Ньютона:
![]() =
=![]() .
.
Правая часть
формулы называется разложением
натуральной степени бинома.
Коэффициенты
![]() называются биномиальными
коэффициентами.
называются биномиальными
коэффициентами.
Отметим некоторые характерные особенности формулы Ньютона.
1. Правая часть
формулы Ньютона содержит (n
+ 1)
слагаемых. 2. ![]() –
формула (k
+ 1)
члена разложения бинома Ньютона. 3. Показатели
степени при a
в каждом следующем члене разложения
на единицу меньше, чем в предыдущем,
показатели степени при b
на единицу больше. Сумма
показателей степени при a
и b
в каждом члене разложения равна
n. 4. Биномиальные
коэффициенты разложения, одинаково
удаленные от конца разложения, равны,
так как по свойству сочетаний
=
–
формула (k
+ 1)
члена разложения бинома Ньютона. 3. Показатели
степени при a
в каждом следующем члене разложения
на единицу меньше, чем в предыдущем,
показатели степени при b
на единицу больше. Сумма
показателей степени при a
и b
в каждом члене разложения равна
n. 4. Биномиальные
коэффициенты разложения, одинаково
удаленные от конца разложения, равны,
так как по свойству сочетаний
=
![]() . 5. Сумма
всех биномиальных коэффициентов равна
2n,
где n
– показатель
бинома.
. 5. Сумма
всех биномиальных коэффициентов равна
2n,
где n
– показатель
бинома.
2.1. Перестановки, размещения и сочетания Вопросы для повторения
1. Что называется перестановкой?
2. Что называется размещением?
3. Что называется сочетанием?
2.1. Вычислить:
 .
.
Решение
=
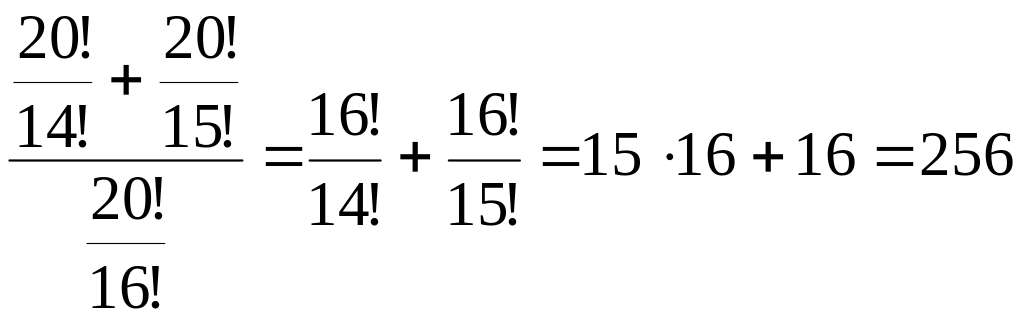 .
.
2.2. Сколько различных двузначных чисел можно образовать из цифр 1, 2, 3, 4 при условии, что в каждом числе нет одинаковых цифр?
Решение
Число различных
двузначных чисел равно числу размещений
из 4 элементов по 2, т.е.
![]() .
Положим n =
4, k
= 2. Получим
.
Положим n =
4, k
= 2. Получим
![]() =
=
=
=
![]() =4
3 = 12.
=4
3 = 12.
2.3. Сколько шестизначных чисел, кратных пяти, можно составить из цифр 1, 2, 3, 4, 5, 6 при условии, что в числе цифры не повторяются.
Решение
Цифра пять обязана стоять на последнем месте. Остальные пять цифр могут стоять на оставшихся пяти местах в любом порядке. Следовательно, искомое число шестизначных чисел, кратных пяти, равно числу перестановок из пяти элементов. Получим Р5 = 5! = 1 2 3 4 5 = 120.
2.4. Группу курсантов должна экзаменовать по математике комиссия из двух преподавателей. Сколькими способами может быть составлена такая комиссия, если в училище пять преподавателей по математике?
Решение
Способы составления комиссии отличаются друг от друга хотя бы одним преподавателем, т.е. комиссия – это подмножество, состоящее из двух различных элементов, множества, состоящего из 5 различных элементов. Число таких способов будет
![]() .
.
2.5. Найти n,
если
![]()
2.6. В розыгрыше первенства по футболу было сыграно 153 матча. Каждые две команды встречались между собой один раз. Сколько команд участвовало в розыгрыше первенства?
2.7. На пять сотрудников выданы три путевки. Сколькими способами их можно распределить, если:
1) все путевки различны;
2) все путевки одинаковы?
2.8. Во взводе три сержанта и 20 солдат. Сколькими способами можно выделить одного сержанта и трех солдат для патрулирования?
2.9. Во взводе 25 человек. Нужно выбрать замкомвзвода, журналиста и книгоношу. Сколькими способами это можно сделать?
2.10. Из цифр 1, 2, 3, 4, 5 составлены различные пятизначные числа, не содержащие одинаковых цифр. Сколько среди этих чисел таких, которые: 1) начинаются цифрой 3; 2) не начинаются цифрой 5; 3) начинаются с числа 54; 4) не начинаются с числа 54; 5) являются четными; 6) делятся на 4?
2.11 Сколько различных трехцветных флагов с тремя горизонтальными полосами можно получить, если использовать: 1) три цвета; 2) четыре цвета?
