Уровни реалистичности изображений

Псевдофотореалистичное изображение (shading, rendering) – закраска с учетом моделируемых источников света. Интенсивность закраски (ярче, темнее) зависит от типа моделируемого источника света и взаимной ориентации поверхностей объекта и источников света.

Модели источников света:

• Точеченый источник (Солнце, лампа)

• Распределенный источник (группа ламп)

• Рассеянный естественный свет – наиболее простая модель, так как обеспечивает постоянное освещение всех поверхностей, независимо от их ориентации.

Для повышения реалистичности изображения используются тени, которые отбрасывает объект, освещенный точечным источником света.

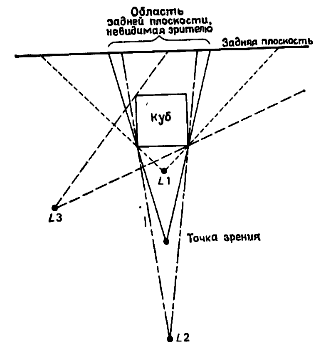
Наблюдателю видны тени от источников света L1 и L3.

Таким образом, если объект А отбрасывает тень на Б, то А находится между Б и источником света.

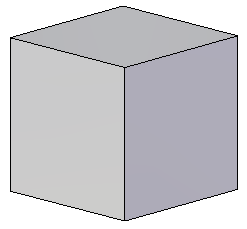
Следующий способ повышения реалистичности изображения – воспроизведение свойств поверхности: матовость, блеск, отражение, полупрозрачность, фактура. Это уже фотореалистичные изображения (rendering, ray trace).

7. Алгоритмы удаления скрытых линий и поверхностей

Дано: 3D-объем и видовые параметры, описывающие тип проекции, проекционную плоскость и т.д.

Требуется: определить, какие ребра и поверхности объекта видимы, если смотреть из центра проекции (для центральных проекций) или вдоль направления проецирования (для параллельных проекций).

Есть два основных подхода к решению задачи для объекта, представленного совокупностью n-угольных граней:

1. Необходимо определить, какая грань видна в каждой точке разрешения экрана дисплея. Чтобы выяснить, какая грань является ближайшей к наблюдателю, необходимо проверить все n граней для каждой точки разрешения экрана. Для N таких точек число проверок пропорционально произведению n*N, где N ~ 2 000 000 (алгоритм работает в пространстве изображений)

2. Каждая из n граней сравнивается с оставшимися (n – 1) гранями. В этом случае число проверок пропорционально n², где n ~ 100 000 - 200 000 (алгоритм работает в пространстве объекта)

Упрощение сравнения по глубине. Перспективное преобразование.

Удаление скрытых поверхностей должно проводиться в трехмерном пространстве до проекцирования на плоскость, при котором теряется информация о Z-координате, необходимая для выполнения сравнения по глубине.

Основное сравнение по глубине можно свести к решению следующей задачи: закрывает ли одна из двух заданных точек P₁(x₁,y₁,z₁) и P₂(x₂,y₂,z₂) другую?

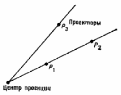Иначе: лежат ли точки P₁(x₁,y₁,z₁) и P₂(x₂,y₂,z₂) на одном и том же проекторе?

Если лежат, то сравнивая z₁ и z₂, можно определить, какая из двух точек ближе к наблюдателю.

При параллельном проецировании (проекторы параллельны оси Z) точки лежат на одном проекторе, если , .

При центральном проецировании (проекторы выходят из начала координат) точки лежат на одном проекторе, если , (надо сделать 4 операции деления!).

Лишних операций можно избежать, если провести такое преобразование трехмерного объекта, при котором параллельная проекция преобразованного объекта представляла бы то же самое, что и центральная проекция исходного объекта. Преобразование деформирует объект и переносит центр проекции в бесконечность в направлении –Z, при этом проекторы оказываются параллельными.

Д о преобразования: После преобразования:

После преобразования куб искажается так, что сохраняется относительная глубина, прямые линии и плоскости, и в то же время производится перспективное укорачивание.

Матрица преобразует нормированный видимый объем (пирамиду) при центральной проекции в прямоугольный параллелепипед, который определяется соотношениями: , , (*).

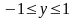Однако отсечение нельзя производить относительно прямоугольного параллелепипеда (*), так как деление на z, выполняемое в матрице М, приводит к потере информации, необходимой для определения знака z-координаты точки. Отсечение относительно нормированного видимого объема можно выполнить до преобразования М, а затем результат умножить на М.

Далее можно приступить к удалению скрытых поверхностей, считая, что теперь мы работаем только с параллельными проекциями.

Примечание об однородных координатах:

Пространство: (X,Y,Z,W)

Нормированные координаты: , ,

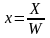Отсекающие пределы: , , .
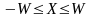
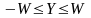