
- •Cовременный подход к конструированию (cad/cam/cae/pdm)
- •Технологии cad/cam/cae
- •2. Технологии моделирования в mcad-системах
- •Технологии описания 3d-геометрии
- •Моделирование на основе истории построений
- •Моделирование без истории построений
- •То, что вы видите, не всегда есть то, что вы получаете ...
- •4. Параметрическое и ассоциативное конструирование Способы создания параметризованной геометрической модели
- •Параметрическое конструирование с полным набором связей или “жесткая” параметризация (Parametric Design)
- •Параметрическое конструирование с неполным набором связей или “мягкая” параметризация (Variational Design)
- •Ассоциативное конструирование (Associative Design)
- •Ассоциативная геометрия (Associative Geometry)
- •Объектно-ориентированное конструирование (Feature-Based Modeling)
- •5. Состав и инструменты системы геометрического моделирования (сгм)
- •Геометрическое моделирование
- •Параметрическое и объектно-ориентированное моделирование
- •Сборочное конструирование
- •Анализ свойств модели
- •Создание и оформление чертежей
- •6. Методы создания реалистичных трехмерных изображений
- •Методы представления отношений по глубине
- •Параллельные проекции
- •Перспективные проекции
- •Уровни реалистичности изображений
- •7. Алгоритмы удаления скрытых линий и поверхностей
- •Упрощение сравнения по глубине. Перспективное преобразование.
- •Исключение сравнения по глубине с помощью оболочек
- •Алгоритм сортировки по глубине
- •Алгоритм, использующий z-буфер
- •Алгоритм построчного сканирования
- •Эффективность алгоритмов
- •8. Модели расчета освещенности граней в пространстве
- •Диффузное отражение и рассеянный свет
- •Зеркальное отражение
- •9. Закраска полигональной сетки
- •Однотонная закраска
- •Интерполяция значений интенсивности (метод Гуро)
- •Интерполяция вектора нормали (метод Фонга)
- •Расчет теневых участков
- •Поверхности, пропускающие свет
- •Направленное пропускание света
- •Моделирование пропускания света без преломления
- •Идея алгоритма трассировки лучей
- •Детализация поверхности
- •10. Цвет в компьютерной графике
- •Ахроматический цвет
- •Аппроксимация полутонами
- •Хроматический цвет
- •Физика и физиология цвета
- •Цветовой график мко
- •Цветовые модели для растровой графики
- •Модели rgb (Red, Green, Blue) и cmy (Cyan, Magenta, Yellow)
- •Цветовая модель yiq (ntsc)
- •Цветовая модель yuv (pal)
- •Цветовая модель hsv
- •Цветовая модель hls
- •Цветовая модель l*a*b
Однотонная закраска
Вычисляется один уровень интенсивности, который используется для закраски всего многоугольника. При этом предполагается, что:
Источник света находится в бесконечности, и поэтому
 постоянно на всей полигональной грани.
постоянно на всей полигональной грани.Точка зрения находится в бесконечности, и поэтому
 постоянно на всей полигональной грани.
постоянно на всей полигональной грани.Многоугольник представляет реальную моделируемую поверхность, а не является аппроксимацией криволинейной поверхности.
Е сли
условия 1) или 2) являются неприемлемыми,
то можно использовать усредненные
значения
и
,
вычисленные в центре многоугольника.
сли
условия 1) или 2) являются неприемлемыми,
то можно использовать усредненные
значения
и
,
вычисленные в центре многоугольника.
Условие 3) в гораздо большей степени влияет на результат закраски, так как значения интенсивностей для соседних граней могут существенно отличаться, что дает резкий перепад (дискретность) интенсивности на всех граничных ребрах. (AutoShade 1.0)
Интерполяция значений интенсивности (метод Гуро)
Этот метод позволяет устранить дискретность изменения интенсивности (но неполностью).
Закраска по методу Гуро выполняется в 4 этапа:
Вычисление нормали к поверхности.
В
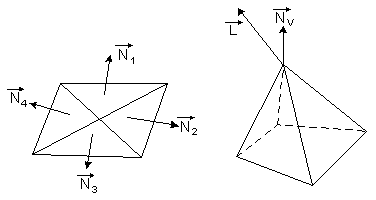 ычисление
нормали в вершинах путем усреднения
нормалей по всем смежным граням.
ычисление
нормали в вершинах путем усреднения
нормалей по всем смежным граням.
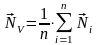 ,
где
n – число прилегающих
к вершине
граней.
В нашем случае:
,
где
n – число прилегающих
к вершине
граней.
В нашем случае:

Вычисление значений интенсивности в вершинах с использованием нормалей в вершинах и какого-либо метода закраски.
Каждый многоугольник закрашивается путем линейной интерполяции значений интенсивности в вершинах сначала вдоль каждого ребра, а затем между ребрами вдоль сканирующей строки.
Ф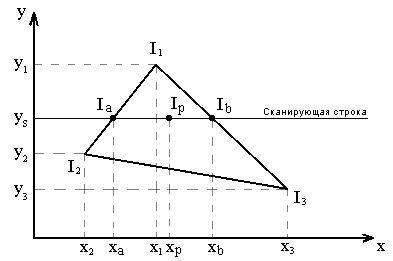 ормулы
интерполяции:
ормулы
интерполяции:
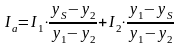
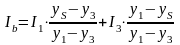

– результат
интерполяции вдоль ребра между значениями
 и
и
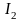 .
.
 – результат
интерполяции вдоль ребра между значениями
и
– результат
интерполяции вдоль ребра между значениями
и
 .
.
– результат интерполяции вдоль сканирующей строки между значениями и .
Интерполяция вдоль ребер легко объединяется с алгоритмом удаления скрытых линий и поверхностей.
Для цветных поверхностей отдельно интерполируется каждая компонента цветовой модели.
Интерполяция вектора нормали (метод Фонга)
Этот
метод основан на интерполяции вектора
нормали
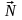 к поверхности вдоль видимого интервала
на сканирующей строке внутри многоугольника.
к поверхности вдоль видимого интервала
на сканирующей строке внутри многоугольника.
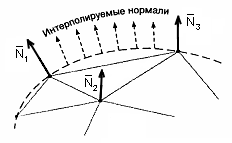
Векторная интерполяция помогает восстановить естественную кривизну поверхности, аппроксимированной многоугольниками.
Для каждой точки грани используется своя «нормаль», направление которой может отличаться от направления истинной нормали к грани. Эти векторы ориентируются таким образом, что являются нормалями некоторой воображаемой выпуклой или вогнутой поверхности, которой принадлежат вершины грани. Таким образом, фактически рассчитывается закраска не плоской грани, а искривленной поверхности, что позволяет эффективно сгладить «граненую» структуру объекта.
Интерполяция выполняется между начальной и конечной нормалями, которые сами являются результатами интерполяции вдоль ребер многоугольника между нормалями в вершинах.
Нормали в вершинах, в свою очередь, вычисляются так же, как и в методе Гуро.
Метод Фонга дает лучший результат для модели зеркального отражения, так как более точно воспроизводятся зеркальные блики.
