
Уровень с
Лестница - стремянка состоит из двух половинок одинаковых по размерам, но разных по массе. Лестницу ставят на горизонтальный пол. На какой максимальный угол можно раздвинуть половинки, если коэффициент их трения о пол равен 0,5? Массы половинок равны 3m и m. (≈ 73,8º)
Проволочный прямоугольный треугольник с углом = 30º поставлен вертикально. По катетам треугольника без трения могут скользить две бусинки связанные нитью (рис. 11.34). Массы бусинок равны m1 = 100 г и m2 = 300 г. Определить силу натяжения нити и угол в положении равновесия. Будет ли положение равновесия устойчивым? ( 79º; 2,65 Н; будет)
Две гладкие наклонные плоскости наклонены под углами 30º и 60º к горизонту и составляют двугранный угол. В этот угол кладут гладкий однородный стержень (рис. 11.35). Какой угол будет составлять стержень с горизонтом в положении равновесия? Будет ли положение равновесия устойчивым? (30º; не будет)
Д
 иск
насажен на горизонтальный вал. Радиус
диска равен 20 см, а радиус вала –
2 см. Для того, чтобы стащить диск с
вала, его нужно тянуть с силой 100 Н. Для
облегчения этой операции к ободу диска
прикладывают касательную силу 8 Н и
одновременно тянут его с силой F.
При каком значении F диск
начнет сниматься с вала? (60 Н)
иск
насажен на горизонтальный вал. Радиус
диска равен 20 см, а радиус вала –
2 см. Для того, чтобы стащить диск с
вала, его нужно тянуть с силой 100 Н. Для
облегчения этой операции к ободу диска
прикладывают касательную силу 8 Н и
одновременно тянут его с силой F.
При каком значении F диск
начнет сниматься с вала? (60 Н)Два одинаковых тяжелых ящика лежат на полу. Их пытаются сдвинуть с места, вставив между ними лом (рис. 11.36). Какой из ящиков сдвинется раньше? (Правый)
Невесомый стержень длиной l вращается с постоянной скоростью вокруг вертикальной оси О, проходящей через один из его концов. На другом конце стержня укреплен диск, который катится по горизонтальной поверхности (рис. 11.37). Масса диска m, коэффициент трения между диском и поверхностью . Найти момент силы на оси О. Ось диска составляет угол со стержнем.
![]()
Т
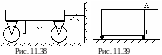 ележка
приводится в движение пружиной как
показано на рисунке. В начальном
состоянии тележка удерживается нитью,
а пружина растянута силой F.
Точка крепления пружины к колесу
находится на расстоянии l
над центром колеса (рис. 11.38). Радиус
колеса тележки равен R,
а масса тележки - m. С каким
ускорением начнет двигаться тележка,
если перерезать нить? Массой колес
пренебречь. Считать, что колеса не
проскальзывают.
ележка
приводится в движение пружиной как
показано на рисунке. В начальном
состоянии тележка удерживается нитью,
а пружина растянута силой F.
Точка крепления пружины к колесу
находится на расстоянии l
над центром колеса (рис. 11.38). Радиус
колеса тележки равен R,
а масса тележки - m. С каким
ускорением начнет двигаться тележка,
если перерезать нить? Массой колес
пренебречь. Считать, что колеса не
проскальзывают.
![]()
Однородный прямоугольный ящик лежит на гладкой горизонтальной поверхности на двух опорах. Ящик начинают тянуть горизонтальной силой, приложенной в точке А. Какая из опор при этом сильнее давит на поверхность? А если сила приложена в точке В (рис. 11.39)? (Правая; левая)
В предыдущей задаче высота ящика равна а, длина - b, а масса - m. Горизонтальную силу прикладывают сначала в точке А, а затем в точке В. При каком значении силы одна из опор оторвется от поверхности?
![]()
Автомобиль имеет две оси, расстояние между которыми равно l. Центр масс автомобиля расположен посередине между осями и на высоте h над землей. Какое максимальное ускорение может развить автомобиль, если ведущая ось: а) задняя; б) передняя? Коэффициент трения между колесами и дорогой равен , размерами и массой колес пренебречь.
![]()
Автомобиль массой М поднимается с постоянной скоростью вверх по дороге, образующей угол с горизонтом. Найти силу взаимодействия ведущих (задних) колес с дорогой. Расстояние между осями колес автомобиля L, центр масс находится посередине между осями колес и на высоте h. На передние колеса сила трения не действует.
![]()
Какой максимальной длины доску можно забить между двумя вертикальными стенами. Расстояние между стенами равно l, коэффициент трения между ними и доской равен , массой доски пренебречь (рис. 11.40).
![]()
Я
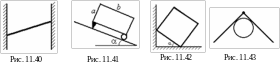 щик
размерами a
b стоит с одной
стороны на колесиках, а с другой - на
жестком упоре. Ящик ставят на наклонную
плоскость колесиками вниз (рис. 11.41).
При этом он начинает скатываться, когда
угол наклона плоскости равен
= 15º. При каком угле наклона начнет
скатываться ящик, если его поставят на
наклонную плоскость колесиками вверх?
Принять b = 2a.
Размерами колес и упора пренебречь.
щик
размерами a
b стоит с одной
стороны на колесиках, а с другой - на
жестком упоре. Ящик ставят на наклонную
плоскость колесиками вниз (рис. 11.41).
При этом он начинает скатываться, когда
угол наклона плоскости равен
= 15º. При каком угле наклона начнет
скатываться ящик, если его поставят на
наклонную плоскость колесиками вверх?
Принять b = 2a.
Размерами колес и упора пренебречь.
![]()
Кубик стоит наклонно в углу комнаты (рис. 11.42). При каком наименьшем значении угла возможно такое равновесие, если коэффициент трения везде одинаков и равен ?
![]()
Два одинаковых однородных стержня соединены шарнирно и лежат на гладком горизонтальном цилиндре, радиус которого равен R (рис. 11.43). В положении равновесия угол между стержнями равен 90º. Какова длина стержней? Устойчиво ли такое положение равновесия? (L = 4R; устойчиво)
Г
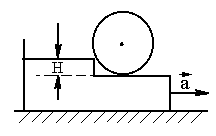 оризонтальная
доска имеет ступеньку высотой Н, в
которую упирается свободно лежащий на
доске однородный цилиндр радиуса R >
H. Доску двигают горизонтально с
ускорением а. Определить максимально
возможное ускорение аmax, при
котором цилиндр еще не будет подниматься
на ступеньку. Трением пренебречь.
оризонтальная
доска имеет ступеньку высотой Н, в
которую упирается свободно лежащий на
доске однородный цилиндр радиуса R >
H. Доску двигают горизонтально с
ускорением а. Определить максимально
возможное ускорение аmax, при
котором цилиндр еще не будет подниматься
на ступеньку. Трением пренебречь.
![]()
Три одинаковых цилиндра сложены вместе и находятся между двумя вертикальными стенами, удерживаясь силами трения (рис. 11.44). Считая коэффициент трения везде одинаковым, найти при каком минимальном значении коэффициента трения возможно такое равновесие?
![]()
Т
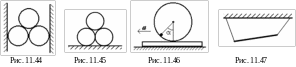 ри
одинаковых бревна сложены вместе и
лежат на горизонтальной поверхности
как показано на рис. 11.45. При каком
коэффициенте трения это возможно,
считая его везде одинаковым.
ри
одинаковых бревна сложены вместе и
лежат на горизонтальной поверхности
как показано на рис. 11.45. При каком
коэффициенте трения это возможно,
считая его везде одинаковым.
![]()
Невесомый обруч, к которому прикреплен небольшой грузик, стоит на доске, движущейся с горизонтальным ускорением а (рис. 11.46). Угол известен и постоянен. Найти ускорение. Обруч по доске не скользит.
![]()
Н
 еоднородный
стержень висит на двух нитях как показано
на рис. 11.47. Построением найти центр
тяжести стержня.
еоднородный
стержень висит на двух нитях как показано
на рис. 11.47. Построением найти центр
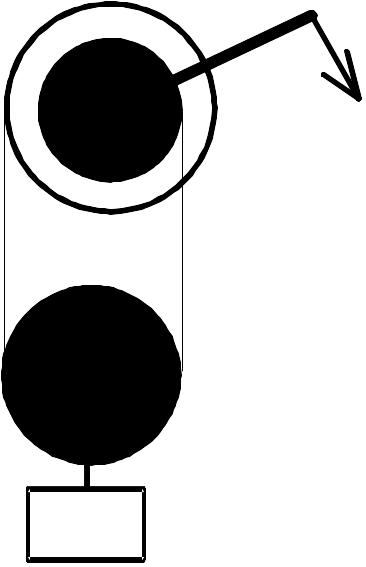
тяжести стержня.Какой груз можно поднять с помощью дифференциального ворота, прикладывая к рукоятке силу 2,5 Н? Длина рукоятки равна 1 м, радиус большого цилиндра - 20 см, радиус малого - 10 см, момент силы трения на оси ворота составляет 20% от момента приложенной силы. (40 Н)
Стержень, шарнирно прикрепленный к полу, опирается на лежащий на полу цилиндр (рис. 11.48). При каком максимальном значении угла наклона стержня возможно равновесие системы, если коэффициент трения между стержнем и цилиндром равен . Трение между цилиндром и полом велико.
![]()
З
 аторможенный
блок, через который перекинута нить с
грузами массой m1
и m2 на концах,
уравновешен на равноплечных весах
(рис. 11.49). На сколько следует изменить
массу гирь на другой чашке весов, чтобы
равновесие сохранилось после освобождения
блока?
аторможенный
блок, через который перекинута нить с
грузами массой m1
и m2 на концах,
уравновешен на равноплечных весах
(рис. 11.49). На сколько следует изменить
массу гирь на другой чашке весов, чтобы
равновесие сохранилось после освобождения
блока?
![]()
Невесомые стержни АВ и ВС соединены шарнирно между собой и с вертикальной стенкой. Угол между стержнями равен . К середине стержня АВ подвешен груз массой m (рис. 11.50). Определить силы давления стержня АВ на шарниры А и В.
![]()
Невесомый стержень АВ шарнирно прикреплен к стене в точке А и удерживается под углом 45° к стене горизонтальной растяжкой ВС (рис. 11.51). В точках B и D к стержню через неподвижный блок подвешен груз массой m (точка D - середина стержня). Найти силу натяжения растяжки ВС и силу реакции в шарнире. (T = 0,75mg; F = 1,25mg)
В стену на одной вертикальной линии вбито два гвоздя. На них вешают тонкий обруч массой m, как показано на рис. 11.52. С какой силой обруч давит на гвозди, если расстояние между гвоздями равно радиусу обруча? (
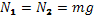 )
)Какой минимальной силой можно опрокинуть через ребро однородный куб массой m, лежащий на горизонтальной поверхности? Каким должен быть при этом коэффициент трения куба о поверхность?
![]()
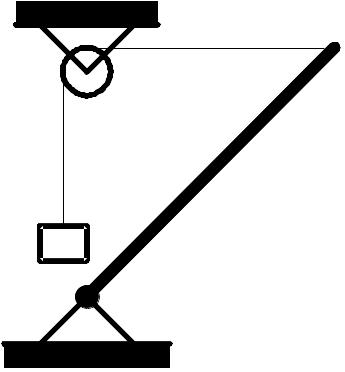
Однородный шарнирно закрепленный стержень удерживается под углом 450 к горизонту горизонтальной нитью, перекинутой через неподвижный блок. Для удержания стержня в таком положении на другой конец нити надо повесить груз массой m. Какой груз должен висеть на нити, чтобы удержать стержень в горизонтальном положении? Шарнир и ось блока находятся на одной вертикали. (
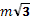 )
)Однородная тонкая пластинка имеет форму треугольника со сторонами 13 см, 14 см, 15 см. На каком расстоянии от второй стороны находится центр тяжести пластинки? (4 см)
Каким должен быть минимальный коэффициент трения, чтобы клин, заколоченный в бревно, не выскакивал из него? Угол при вершине клина = 30°. ( 0,27)
Гладкий стержень согнут в виде угла и расположен так, что биссектриса угла вертикальна. На угол надели петлю из легкой нити, на которой закреплен небольшой груз (рис. 11.53). Определить угол , который образует нить, отходящая от груза, в положении равновесия.
= 180° - 2
К
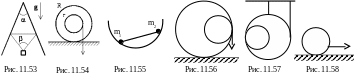 атушку
тянут за нитку, пропущенную в отверстие
стола (рис. 11 54). При каком значении
коэффициента трения катушка будет
проворачиваться на месте. Радиусы
катушки R и r.
Массой катушки пренебречь.
атушку
тянут за нитку, пропущенную в отверстие
стола (рис. 11 54). При каком значении
коэффициента трения катушка будет
проворачиваться на месте. Радиусы
катушки R и r.
Массой катушки пренебречь.
![]()
На внутренней поверхности гладкой сферы лежит невесомый стержень с маленькими шариками массами m1 и m2 на концах (рис. 11.55). Длина стержня равна радиусу сферы. Найти угол между стержнем и горизонталью.
![]()
Однородная пластина имеет форму круга радиусом R. В пластине вырезано отверстие радиусом R/2, касающееся края пластины. Пластину поставили вертикально на горизонтальную поверхность. Какую вертикальную силу в точке касания надо приложить к пластине, чтобы центры пластины и отверстия находились на одном горизонтальном уровне (рис. 11.56)? Масса пластины с вырезом равна m.
![]()
Тонкий однородный диск радиусом R подвешен на двух нитях, как показано на рис. 11.57. В диске вырезано отверстие радиусом R/2, касающееся края диска. Найти силы натяжения нитей, если толщина диска равна h, а плотность материала диска ρ.
![]()
Шар радиусом R и массой m движется поступательно по горизонтальной поверхности под действием постоянной силы натяжения нити F. Точка закрепления нити находится на высоте h (рис. 11.58). Чему равно ускорение шара?

![]()
Прямоугольный брусок с размерами а х b равномерно тянут по горизонтальной поверхности за веревку, угол наклона которой может меняться. Коэффициент трения равен . При каком угле наклона брусок начнет приподниматься?
![]()
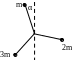
Вертушка состоит из трех легких одинаковых стержней, скрепленных в одной точке. Углы между стержнями одинаковы. На свободных концах стержней закреплены маленькие шарики массами m, 2m и 3m. Вертушка может свободно вращаться вокруг горизонтальной оси, проходящей через точку скрепления стержней. Чему равен угол α в положении равновесия системы. (30º)
