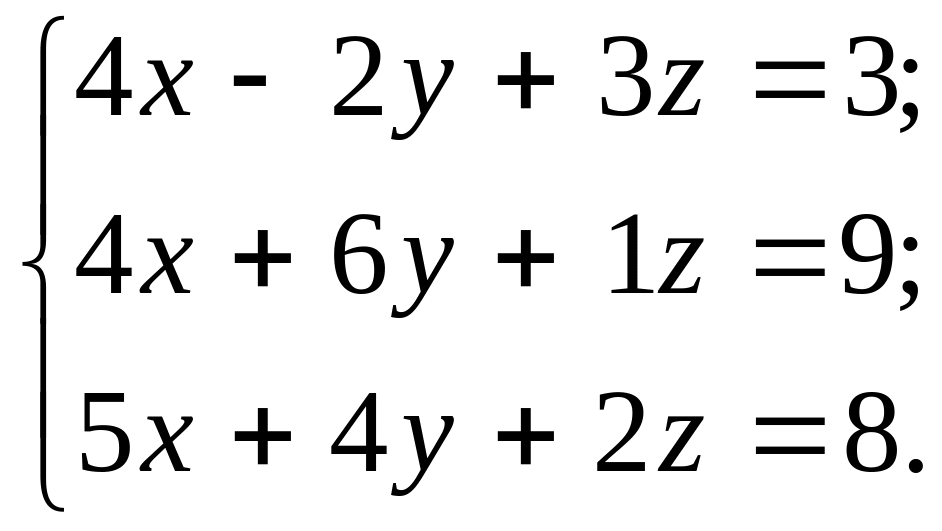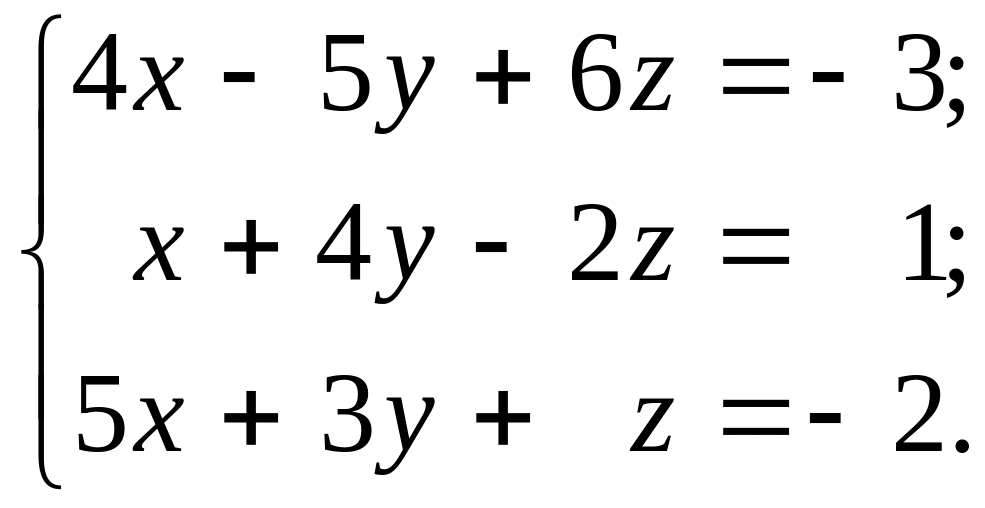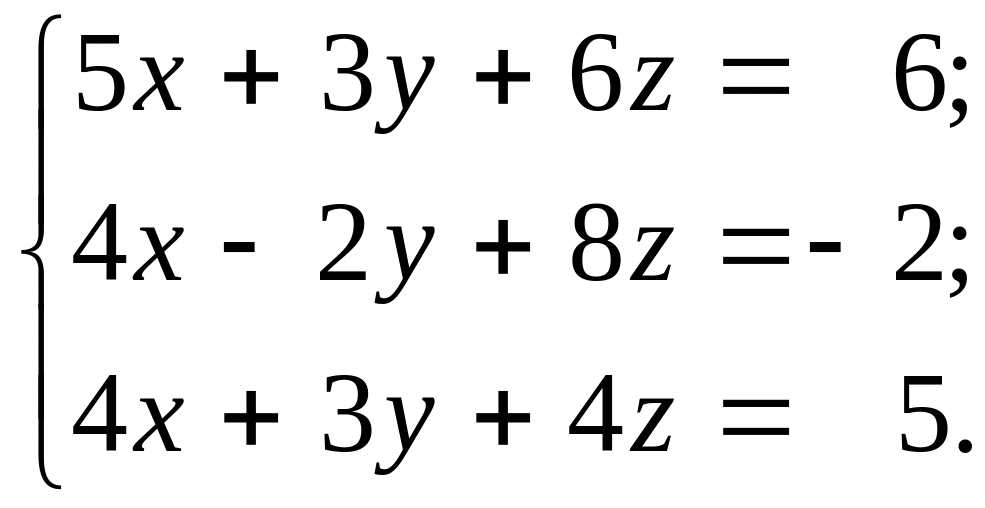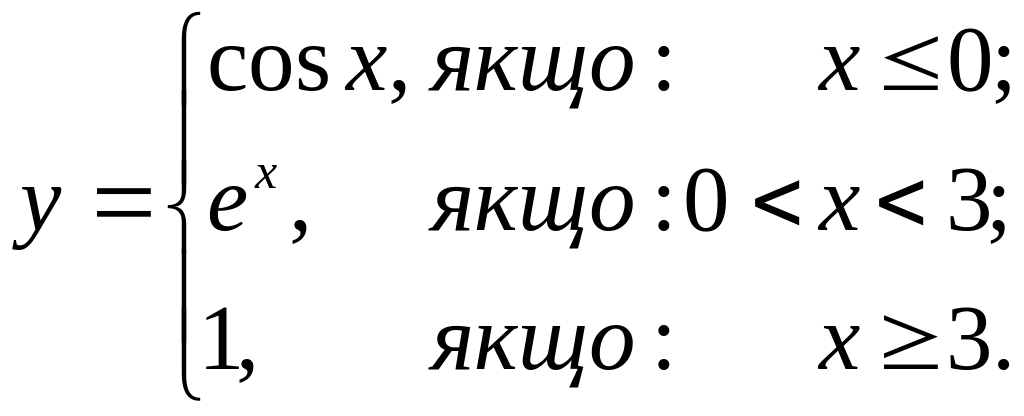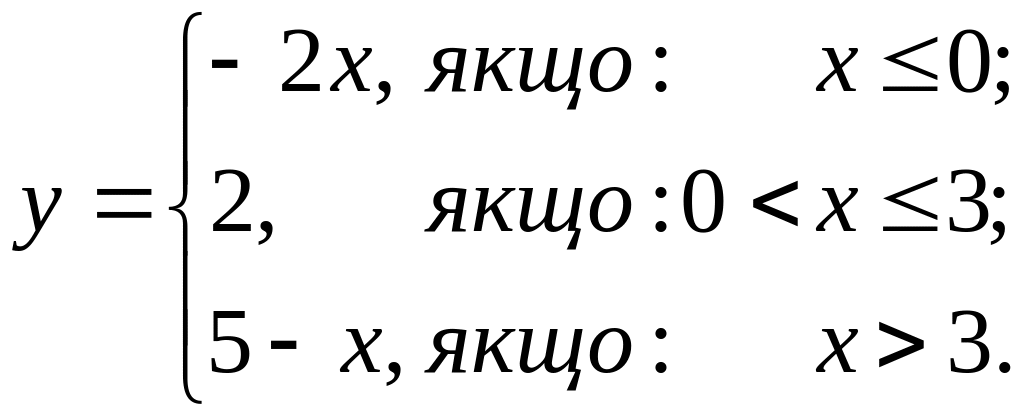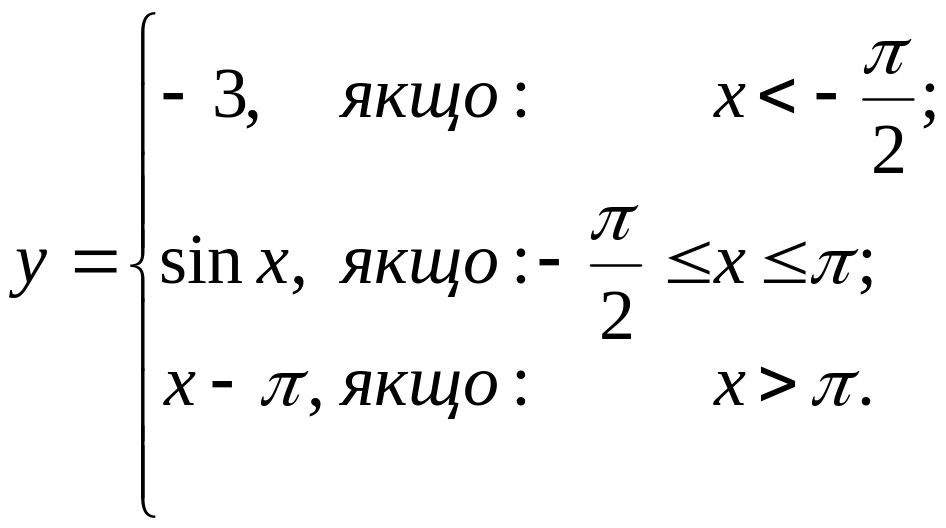Індивідуальне семестрове завдання
з вищої математики
Галузь знань – 0306 – „Менеджмент і адміністрування”
Напрям підготовки – 6.030601 „Менеджмент”
освітньо-кваліфікаційний рівень – бакалавр
(денна форма навчання)
на І семестр
МОВ, МОТ, МВД-12
доцент: Сукач Т.Н.
Алчевськ, 2012
1. Решить систему линейных алгебраических уравнений:
Методом Крамера; Методом Гаусса; Матричным методом.
1)
|
2)
|
3)
|
4)
|
5)
|
6)
|
7)
|
8)
|
9)
|
10)
|
11)
|
12)
|
13)
|
14)
|
15)
|
16)
|
17)
|
18)
|
19)
|
20)
|
21)
|
22)
|
23)
|
24)
|
25)
|
26)
|
27)
|
28)
|
29)
|
30)
|
2. Дані про виконання балансу за звітний період (в умов. Грош. Од.) наведено в таблиці:
Галузь виробництва |
Розподіл випуску продукції в галузях |
Обсяг кінцевої продукції |
Обсяг валової продукції |
|
1 |
2 |
|||
1 |
9 |
25 |
50+N |
100 |
2 |
8 |
27 |
165 |
200 |
(N – номер варіанту).
Обчислити необхідний обсяг валової продукції кожної галузі, якщо обсяг кінцевої продукції першої галузі збільшиться вдвоє, а другої – не зміниться.
3. Даны вершины треугольника АВС. Найти: 1) длину стороны ВС; 2) уравнение ВС; 3) уравнение высоты АМ; 4) длину высоты АМ; 5) площадь треугольника АВС; 6) величину угла В; 7) координаты точки пересечения медиан треугольника.
№ |
А |
В |
С |
№ |
А |
В |
С |
1 |
1, 1 |
-3,-2 |
3,-4 |
16 |
3, 0 |
-1,-6 |
-3, 1 |
2 |
1,-1 |
-3, 1 |
3, 3 |
17 |
3, 1 |
-1, 4 |
-3,-1 |
3 |
1, 2 |
-3,-1 |
0,-2 |
18 |
3,-1 |
-1, 1 |
0,-4 |
4 |
-1, 1 |
-3,-2 |
2,-2 |
19 |
0, 3 |
6,-1 |
-1,-3 |
5 |
-1, 2 |
6, 0 |
0,-2 |
20 |
0,-3 |
4, 6 |
-1,-2 |
6 |
-1, 0 |
3, 4 |
6,-2 |
21 |
-3, 0 |
2, 3 |
6,-1 |
7 |
0, 1 |
4, 3 |
6,-1 |
22 |
3, 4 |
-1, 1 |
2,-1 |
8 |
1, 0 |
-3,-2 |
3,-3 |
23 |
4, 3 |
6,-1 |
1, 0 |
9 |
0,-1 |
-6, 1 |
-4,-5 |
24 |
4,-3 |
1, 1 |
7, 2 |
10 |
2, 1 |
-3, 0 |
-1,-5 |
25 |
-3, 4 |
0,-2 |
6, 1 |
11 |
2,-1 |
0, 6 |
-5, 0 |
26 |
1, 0 |
0, 2 |
-1, 1 |
12 |
2, 3 |
-2, 5 |
-6, 0 |
27 |
0, 1 |
-2, 0 |
-1,-1 |
13 |
-3, 2 |
2, 3 |
6, 1 |
28 |
2, 1 |
0, 3 |
-1, 2 |
14 |
3, 2 |
-2, 5 |
-1, 5 |
29 |
-1, 0 |
2, 2 |
5,-2 |
15 |
-3,-2 |
0,-5 |
5, 0 |
30 |
0,-2 |
5, 2 |
7,-4 |
4. Даны вершины пирамиды ABCD. Найти: 1) периметр основания АВС; 2) угол между ребрами АВ и AD; 3) площадь грани АВС; 4) уравнение плоскости АВС; 5) проекцию АВ на AD; 4) объем пирамиды ABCD; 5) длину высоты пирамиды DO; 6) канонические уравнения прямой, проходящей через точку D перпендикулярно плоскости ABC.
№ |
A |
B |
C |
D |
1 |
1, 0, 0 |
0, 2, 1 |
2, 3, 4 |
-2, 1, 3 |
2 |
2, 0, 0 |
1, 2, 2 |
-1, 1, 1 |
3,-1, 1 |
3 |
3, 0, 0 |
1, 1, 1 |
2, 1, 0 |
-1, 2, 2 |
4 |
-1, 0, 0 |
2, 1, 0 |
3, 2,-1 |
1, 1, 1 |
5 |
-2, 0, 0 |
2, 1, 2 |
3,-1, 2 |
1, 2, 1 |
6 |
-3, 0, 0 |
3, 1, 1 |
2,-1, 2 |
1, 2, -1 |
7 |
1, 1, 0 |
2, 0, 1 |
1, 3, 0 |
0, 0, 4 |
8 |
1, 2, 0 |
-2, 0, 1 |
0, 3, 4 |
3, 1, 2 |
9 |
1, 3, 0 |
3, 1, 2 |
-1, 2, 1 |
-2, 1,-1 |
10 |
1,-1, 0 |
2, 1, 1 |
-1, 2, 2 |
0, 0, 3 |
11 |
1,-2, 0 |
2, 0, 0 |
0,-2, 1 |
4, 1, 2 |
12 |
1,-3, 0 |
3, 0, 1 |
2, 1, 2 |
-1, 2, 3 |
13 |
2, 1, 0 |
3, 2, 2 |
1, 0, 1 |
-1, 3, 3 |
14 |
2, 2, 0 |
1, 3, 1 |
-1, 1, 2 |
3,-1, 3 |
15 |
2,-2, 0 |
-1, 3, 4 |
-1, 4, 2 |
1,-2, 2 |
16 |
-2, 1, 0 |
1,-1, 1 |
2, 2, 2 |
3, 0, 3 |
17 |
-2,-1, 0 |
1, 1,-1 |
3, 2, 1 |
4, 0, 2 |
18 |
2, 0, 1 |
3, 2, 2 |
-1, 1, 0 |
0,-1, 3 |
19 |
3, 0, 1 |
4, 2, 2 |
2,-1, 1 |
-2, 2, 0 |
20 |
1, 0, 1 |
2,-2, 3 |
0, 1, 2 |
3, 3, 0 |
21 |
-2, 0, 1 |
2, 2, 2 |
1, 1, 3 |
-1, 3,-1 |
22 |
-2, 0,-1 |
2,-1, 0 |
1, 1, 1 |
3, 4, 2 |
23 |
2, 0, 2 |
3, 1, 1 |
1, 2,-1 |
-1, 3, 0 |
24 |
3, 0, 2 |
2, 2, 1 |
4, 1, 0 |
-1, 4, 3 |
25 |
3, 0, 4 |
1, 1, 3 |
2,-1,-1 |
4, 2, 1 |
26 |
2, 0, 4 |
1, 1, 2 |
-1, 2, 0 |
0,-1, 3 |
27 |
2, 0, 0 |
0, 0, 0 |
1,-1, 0 |
1, 1, 0 |
28 |
0, 0, 1 |
0, 0,-2 |
1, 0, 0 |
0,-1, 1 |
29 |
1, 1,-1 |
1, 0, 0 |
0, 1, 0 |
0, 0, 1 |
30 |
0, 1,-1 |
1,-1, 0 |
2, 1,-1 |
3, 2, 1 |
5. Вычислить (без правила Лопиталя) границы:
1). 
2). 
.
3). 
.
4). 
.
5). 
.
6). 
.
7). 
.
8). 
.
9). 
.
10). 
; 
.
11). 
12). 
13). 
14). 
15). 
16). 
17). 
18). 
19). 
20). 
21). 
22). 
23). 
24). 
25). 
26). 
27). 
28). 
29). 
30). 
6. Исследовать на непрерывность функцию и классифицировать точки разрыва:
1).
|
2). |
3).
|
4).
|
5).
|
6).
|
7).
|
8).
|
9).
|
10).
|
11).
|
12). |
13). |
14).
|
15).
|
16).
|
17).
|
18).
|
19).
|
20).
|
21).
|
22).
|
23). |
24). |
25).
|
26).
|
27).
|
28).
|
29).
|
30).
|
7. Найти производные данных функций:
1). 
2). 
3). 
4). 
5). 
6). 
7). 
8). 
9). 
10). 
11). 
12). 
13). 
14). 
15). 
16). 
17). 
18). 
19). 
20). 
21). 
22). 
23). 
24). 
25). 
26). 
27). 
28). 
29). 
30). 
8. Провести полное исследование функций и построить их графики:
1). 
2). 
3). 
4). 
5). 
6). 
7). 
8). 
9). 
10). 
11). 
12). 
13). 
14). 
15). 
16). 
17). 
18). 
19). 
20). 
21). 
22). 
23). 
24). 
25). 
26). 
27). 
28). 
29). 
30). 
9. Известны общие затраты
производства продукции и функция спроса
на продукцию
(рыночная цена как функция объема
спроса).
Найти точку равновесия (Р*, х*), максимизирующую общую прибыль.
,
.
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
, 
,
,
,
,
,
,
,
,
,
,
,
,
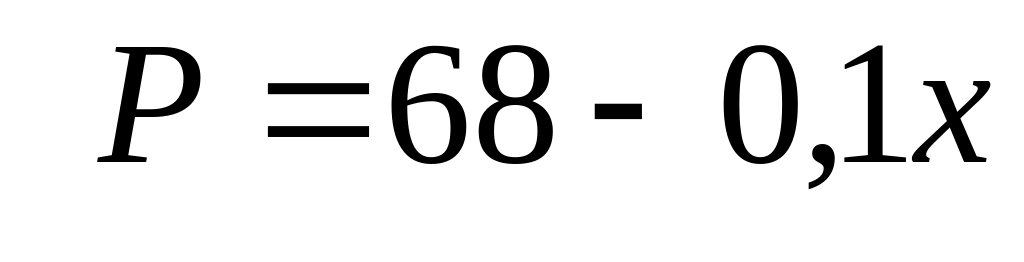
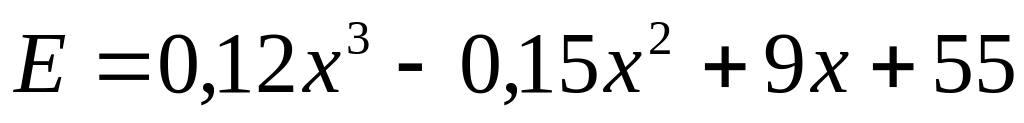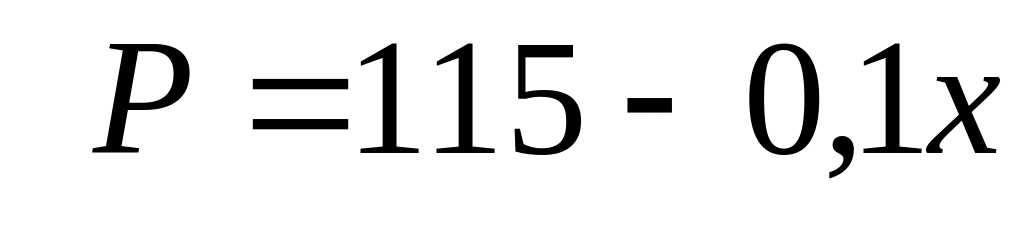
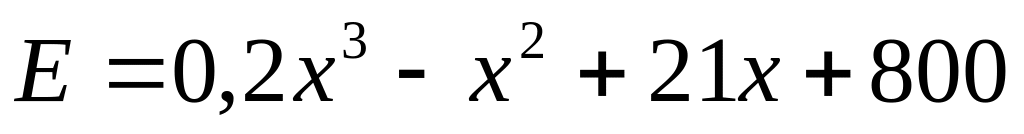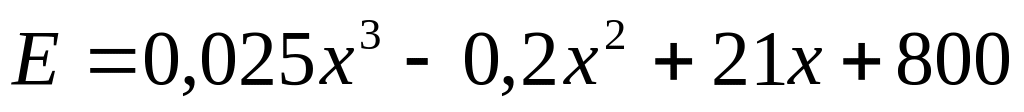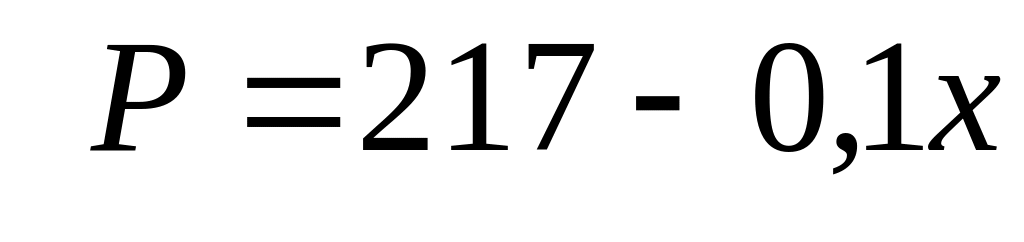
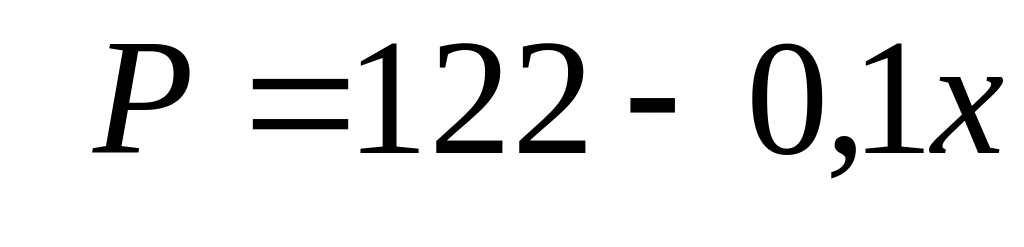
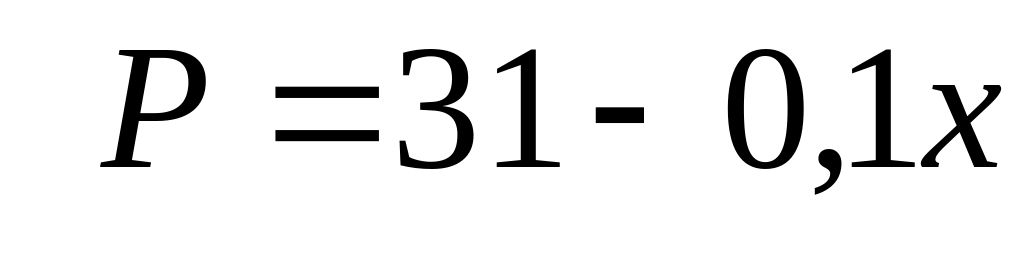
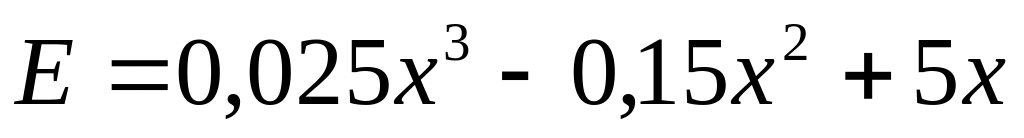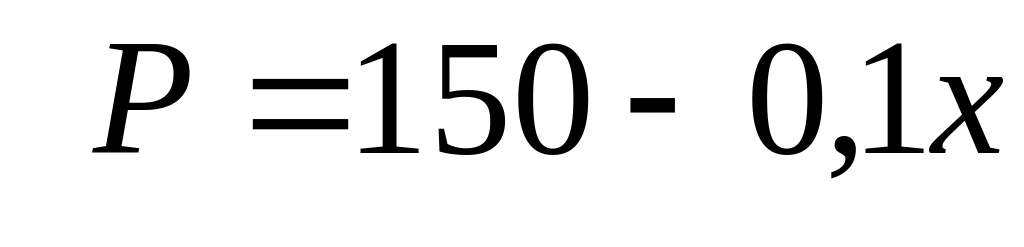
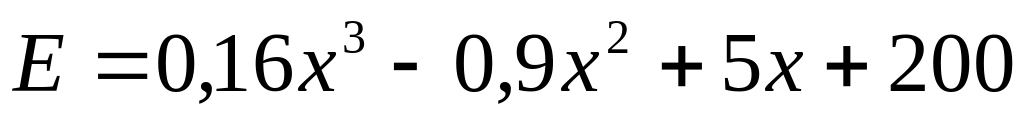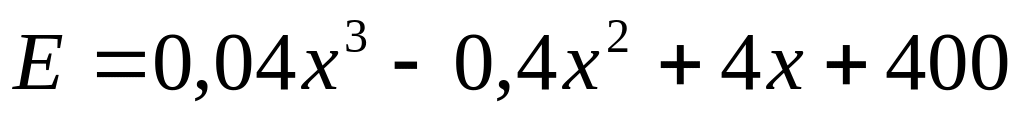