
- •§1. Скалярные и векторные поля.
- •§2. Поверхности и линии уровня.
- •§3. Производная по направлению скалярного поля.
- •Контрольное задание 2.
- •§4. Градиент скалярного поля.
- •Контрольное задание 3.
- •§5. Векторные линии поля.
- •Контрольное задание 4.
- •§6. Линейный интеграл векторного поля.
- •Формула Грина.
- •Контрольное задание 5.
- •§7. Потенциальное векторное поле.
- •Примеры потенциальных полей.
- •Контрольное задание 6.
- •§8. Поток векторного поля.
- •Контрольное задание 7.
- •§9. Дивергенция векторного поля. Соленоидальное векторное поле.
- •Формула Остроградского – Гаусса.
- •Контрольное задание 8.
- •§10. Ротор (вихрь) векторного поля. Формула Стокса.
- •Контрольное задание 9.
- •§11. Операторы Гамильтона и Лапласа.
- •Дифференциальные операции второго порядка.
- •Запись дифференциальных операций второго порядка в операторной форме.
- •Контрольное задание 10.
- •Ответы к контрольным заданиям.
- •Список литературы.
- •Оглавление.
- •Скалярные и векторные поля. 4
Контрольное задание 8.
1. Найти дивергенцию
поля
![]() .
Исследовать положение источников и
стоков.
.
Исследовать положение источников и
стоков.
2. Найти поток
векторного поля
![]() через полную поверхность тела,
определяемого неравенствами:
через полную поверхность тела,
определяемого неравенствами:
![]() .
.
3. Найти поток
векторного поля
![]() через полную поверхность тела,
определяемого неравенствами:
через полную поверхность тела,
определяемого неравенствами:
![]() .
.
4. Найти поток
векторного поля
![]() через полную поверхность тела,
определяемого неравенствами:
через полную поверхность тела,
определяемого неравенствами:
![]() .
.
5. Вычислить поток
векторного поля
![]() :
а) через боковую поверхность конуса
:
а) через боковую поверхность конуса![]() в направлении внешней нормали;
б) через всю поверхность
сферы
в направлении внешней нормали;
б) через всю поверхность
сферы
![]() в направлении внешней нормали.
в направлении внешней нормали.
§10. Ротор (вихрь) векторного поля. Формула Стокса.
Пусть
- векторное поле, заданное в конечной
области G
с гладкой (или кусочно-гладкой) границей
σ и
![]() - единичный вектор внешней нормали к σ
в точке M.
Вектор-функция
- единичный вектор внешней нормали к σ
в точке M.
Вектор-функция
![]()
называется циркуляцией поля по границе области G.
Если существует
предел при стягивании объёма V,
заключённого
внутри
в точку
![]() :
:
![]() ,
,
то вектор
![]() называется ротором или вихрем поля
в точке
и обозначается символом
называется ротором или вихрем поля
в точке
и обозначается символом
![]() .
По определению:
.
По определению:
 .
.
это плотность циркуляции векторного поля по границе области.
Пусть в области G
задано векторное поле
.
Пусть
-
внутренняя точка области G,π
–некоторая плоскость, проходящая через
эту точку.
- единичный вектор внешней нормали к π,
L-
замкнутый
контур, лежащий в плоскости и ограничивающий
область Ф,
такую, что
- внутренняя точка области Ф.
Тогда принимают
 (24)
(24)
В правую часть формулы (24) входят величины, инвариантные относительно выбора системы координат (циркуляция векторного поля вдоль замкнутого контура и площадь плоской области).
Если компоненты
поля
имеют непрерывные частные производные
по
![]() ,
то вектор ротора поля
вычисляется по формуле:
,
то вектор ротора поля
вычисляется по формуле:
![]() . (25)
. (25)
В частности, для
плоского поля
![]() :
:
![]() .
.
Определение 12.
Если в каждой
точке области выполняется равенство
![]() ,
то поле
называется безвихревым.
,
то поле
называется безвихревым.
Теорема. В односвязной области всякое безвихревое поле потенциально.
![]() .
.
Это является необходимым и достаточным условием потенциальности поля в поверхностно односвязной области. Если область не является поверхностно односвязной, то условие не достаточно для потенциальности поля.
Формула Стокса.
Пусть в области G
определено
векторное поле
![]() .
L
– замкнутый контур, расположенный в
области G.
σ – поверхность,
ограниченная контуром L,
гладкая или
кусочно-гладкая.
.
L
– замкнутый контур, расположенный в
области G.
σ – поверхность,
ограниченная контуром L,
гладкая или
кусочно-гладкая.
![]() - единичный вектор нормали на выбранной
стороне поверхности σ
. Пусть
функции
непрерывны вместе со своими частными
производными. Тогда справедлива формула
Стокса:
- единичный вектор нормали на выбранной
стороне поверхности σ
. Пусть
функции
непрерывны вместе со своими частными
производными. Тогда справедлива формула
Стокса:
![]() .
(26)
.
(26)
Ориентация контура L согласована с ориентацией поверхности σ по правилу правого винта. Или:
![]() . (27)
. (27)
Левая часть формулы
Стокса – это циркуляция векторного
поля
вдоль контура L,
а правая
представляет собой поток через поверхность
σ
векторного поля
![]() .
В векторной форме формулу Стокса можно
записать так:
.
В векторной форме формулу Стокса можно
записать так:
![]() . (28)
. (28)
Физический смысл формулы Стокса: циркуляция векторного поля вдоль замкнутого контура равна потоку ротора этого поля через произвольную поверхность, натянутую на этот контур.
Формула Стокса остаётся справедливой и в случае, когда поверхность σ является плоской областью, параллельной какой-нибудь координатной плоскости. Тогда формула Стокса превращается в формулу Грина:
![]() .
.
Пример 22.
Найти ротор векторного поля
![]() и убедиться, что новое поле
и убедиться, что новое поле
![]() является соленоидальным.
является соленоидальным.
Решение. По формуле (25) имеем:
![]() .
.
Вычислим
![]() по формуле (29):
по формуле (29):
![]() .
.
Ответ: Так как
![]() ,
поле
является соленоидальным, ч.т.д.
,
поле
является соленоидальным, ч.т.д.
Пример 23.
Проверить, является ли потенциальным
векторное поле
![]() .
.
Решение. По формуле (25) имеем:

Ответ: данное поле
является потенциальным, т.к.
![]() .
.
Пример 24.
В
Рисунок 17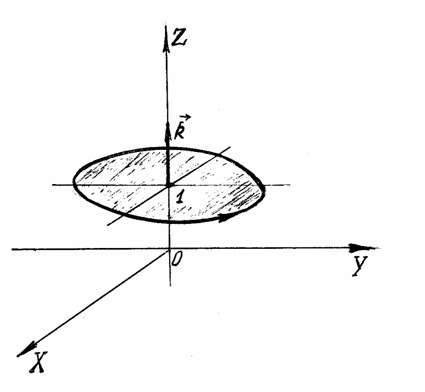
![]() по эллипсу
по эллипсу
![]() .
Обход контура против часовой стрелки,
если смотреть из точки M(0,0,3).
Ответ проверить по формуле
Стокса.
.
Обход контура против часовой стрелки,
если смотреть из точки M(0,0,3).
Ответ проверить по формуле
Стокса.
Решение.
1) По формуле (7): Ц![]() .
.
Примем:
![]() ,
тогда
,
тогда
![]() ,
,![]() .
Ц
.
Ц![]()
![]() .
.
2)По формуле Стокса:
Ц![]() .
.
Вычислим
по формуле (25):![]() .
.
В качестве σ
выберем
плоскость
z=1,
тогда
![]() и
и
![]() .
.
Тогда Ц![]() .
Площадь эллипса с полуосями a
и
b
равна
.
Площадь эллипса с полуосями a
и
b
равна
![]() .
.
Ответ: Ц![]() .
.
П
Рисунок 18
![]()
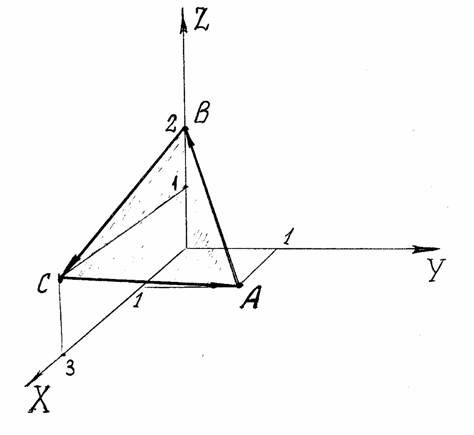 по контуру
треугольника
ABC
, где
A(1,1,0),
B(0,0,2),
C(3,0,1),
двумя способами: 1) с помощью криволинейного
интеграла, 2) по формуле Стокса.
по контуру
треугольника
ABC
, где
A(1,1,0),
B(0,0,2),
C(3,0,1),
двумя способами: 1) с помощью криволинейного
интеграла, 2) по формуле Стокса.
Выяснить, как зависит циркуляция от расположения контура в данном поле.
Решение.
1) По формуле (7):
Ц![]() (см.
рис.17)
(см.
рис.17)
Составим уравнения прямых, содержащих стороны треугольника.
![]()
![]()
![]()
 Ц
Ц![]()
2) Вычислим циркуляцию
по формуле Стокса: Ц
.
В качестве поверхности σ
выберем
плоскость
треугольника ABC.
Тогда
![]() .
Единичный вектор нормали, составляющий
острые углы с осями координат:
.
Единичный вектор нормали, составляющий
острые углы с осями координат:
![]() .
.
Найдём
по формуле (25):![]() ,
,
![]() .
.
Тогда Ц![]() ,
ч.т.д.
,
ч.т.д.
3) Исследуем поведение циркуляции при перемещении нашего контура в пространстве. Для этого используем определение скалярного произведения.
Ц![]() ,
где
–
угол между векторами
и
.
,
где
–
угол между векторами
и
.
Видим, что циркуляция зависит от этого угла . Отсюда следует, что если треугольник ABC перемещается в пространстве параллельно своему исходному положению, то угол не меняется, и циркуляция по контуру остаётся равной 9, а при повороте контура меняется направление вектора , что влечёт изменение циркуляции.
Циркуляция достигнет
максимального значения, когда
![]() ,
т.е. когда
,
т.е. когда
![]() .
В этом случае Ц
.
В этом случае Ц![]() .
.
Если
![]() ,
то Ц=0.
,
то Ц=0.
Ответ:Ц=9,
Ц
![]() .
.
Пример 26.
Вычислить
циркуляцию векторного поля
![]() вдоль линии L
пересечения поверхности
вдоль линии L
пересечения поверхности
![]() и цилиндра
и цилиндра
![]() ,
используя формулу Стокса, если нормаль
к поверхности образует острый угол с
осью OZ.
,
используя формулу Стокса, если нормаль
к поверхности образует острый угол с
осью OZ.
Р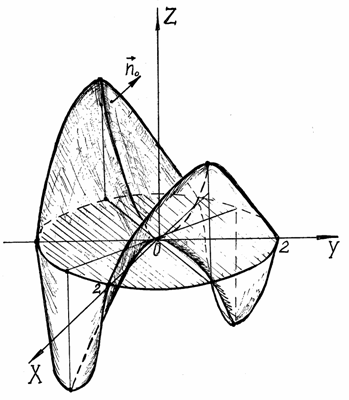 ешение.
ешение.
П
Рисунок 19![]() .
.
Найдём
по формуле (25):
![]() .
.
Л
Рис18![]() .
Нормаль к ней получим по формуле:
.
Нормаль к ней получим по формуле:
![]() ,
где
,
где
![]() .
Т.е
.
Т.е
![]() .
Данный вектор образует острый угол с
осью OZ,
что и требуется по условию задачи.
Тогда
.
Данный вектор образует острый угол с
осью OZ,
что и требуется по условию задачи.
Тогда
![]() ,
т. к.
из уравнения поверхности. Получаем Ц
,
т. к.
из уравнения поверхности. Получаем Ц![]() - поверхностный интеграл первого рода.
- поверхностный интеграл первого рода.
Для его вычисления
спроектируем
на плоскость
XOY.
Проекцией является круг![]() .
.
Имеем
![]() .
.
Тогда: Ц .
.
Ответ: Ц=0.
