
- •§1. Скалярные и векторные поля.
- •§2. Поверхности и линии уровня.
- •§3. Производная по направлению скалярного поля.
- •Контрольное задание 2.
- •§4. Градиент скалярного поля.
- •Контрольное задание 3.
- •§5. Векторные линии поля.
- •Контрольное задание 4.
- •§6. Линейный интеграл векторного поля.
- •Формула Грина.
- •Контрольное задание 5.
- •§7. Потенциальное векторное поле.
- •Примеры потенциальных полей.
- •Контрольное задание 6.
- •§8. Поток векторного поля.
- •Контрольное задание 7.
- •§9. Дивергенция векторного поля. Соленоидальное векторное поле.
- •Формула Остроградского – Гаусса.
- •Контрольное задание 8.
- •§10. Ротор (вихрь) векторного поля. Формула Стокса.
- •Контрольное задание 9.
- •§11. Операторы Гамильтона и Лапласа.
- •Дифференциальные операции второго порядка.
- •Запись дифференциальных операций второго порядка в операторной форме.
- •Контрольное задание 10.
- •Ответы к контрольным заданиям.
- •Список литературы.
- •Оглавление.
- •Скалярные и векторные поля. 4
Формула Грина.
Для плоского векторного поля имеет место следующее утверждение.
Если функции
![]() и их частные производные
и их частные производные
![]() непрерывны в замкнутой области
непрерывны в замкнутой области
![]() Г,
где Г
– граница односвязной области G,
то
Г,
где Г
– граница односвязной области G,
то
![]() - формула
Грина. (10)
- формула
Грина. (10)
![]() обозначает
положительное направление обхода
(против часовой стрелки).
обозначает
положительное направление обхода
(против часовой стрелки).
Пример 12. Используя
формулу Грина, вычислить циркуляцию
векторного поля
![]() по
контуру, состоящему из отрезков OA,
OB
и большей дуги окружности
по
контуру, состоящему из отрезков OA,
OB
и большей дуги окружности
![]() ,
соединяющей точки A
и B,
если
,
соединяющей точки A
и B,
если
![]() ,
,
![]() ,
,
![]() .
.
Р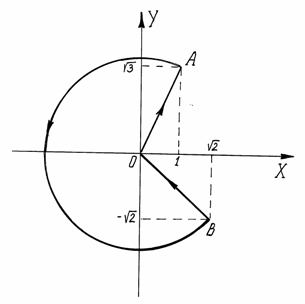 ешение.
ешение.
Рисунок 8![]() .
.
![]() ,
,![]() ;
;
![]() ,
,
![]() .
Ц
.
Ц![]()
 .
.
Проверим ответ,
вычислив циркуляцию непосредственно
по контуру с помощью линейного интеграла:
Ц![]() .
.
![]() .
.
![]()
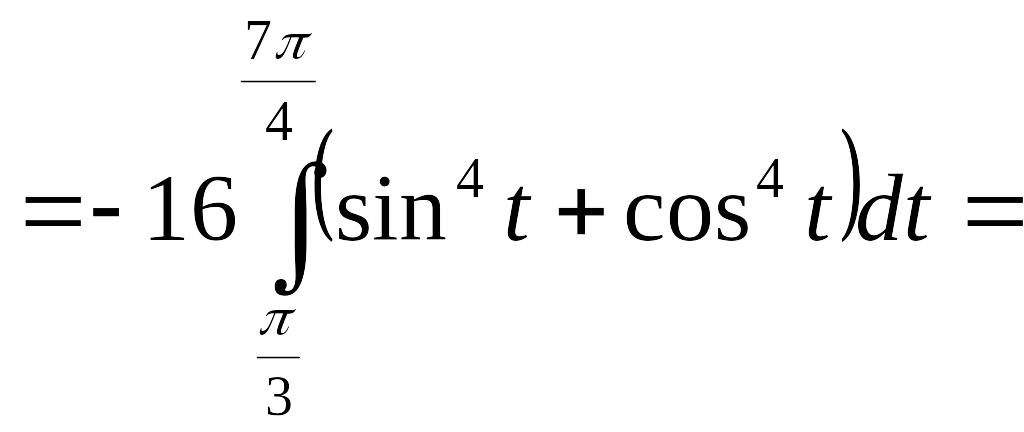
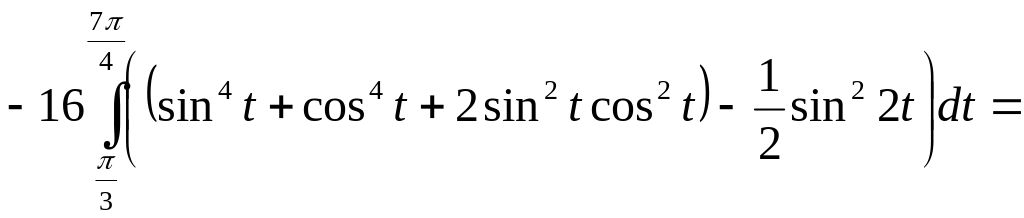
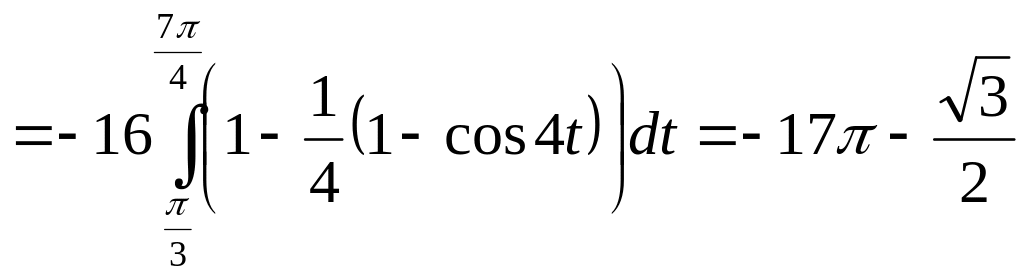 .
.
![]() .
.
Ответ:
Ц![]() .
.
Контрольное задание 5.
Вычислить линейные интегралы векторного поля:
1)
![]() по
ломаной
по
ломаной
![]() .
.
2)
![]() по эллипсу а)
по эллипсу а)
![]() ,
б)
,
б)
![]() .
.
3) Вычислить
циркуляцию векторного поля
![]() вдоль эллипса, полученного от пересечения
цилиндра
плоскостью
вдоль эллипса, полученного от пересечения
цилиндра
плоскостью
![]() в направлении по часовой стрелке, если
смотреть из точки (0;10;0).
в направлении по часовой стрелке, если
смотреть из точки (0;10;0).
4) Вычислить линейный
интеграл векторного поля![]() вдоль ломаной линии ABOC,
где
вдоль ломаной линии ABOC,
где
![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
5) Найти работу
поля
![]() вдоль
части линии пересечения цилиндров
вдоль
части линии пересечения цилиндров
![]() и
и
![]() от точки
от точки![]() через
через
![]() до точки
до точки
![]() .
.
§7. Потенциальное векторное поле.
Определение 7.
Векторное
поле
называется потенциальным в области G,
если существует
такая скалярная функция
![]() ,
что её градиент равен
:
,
что её градиент равен
:![]() .
.
Функция
называется скалярным потенциалом
векторного поля
.
Если
,
то из определения (6) следует, что
![]()
Пусть функции
![]() имеют непрерывные частные производные
в односвязной области G.
Тогда для
потенциального поля
можно доказать эквивалентность следующих
утверждений:
имеют непрерывные частные производные
в односвязной области G.
Тогда для
потенциального поля
можно доказать эквивалентность следующих
утверждений:
1) Имеют место
равенства:
![]() (11)
(11)
Для плоского поля:
![]() . (11.1)
. (11.1)
Это необходимые и достаточные условия потенциальности поля.
2) Циркуляция
векторного поля по любому замкнутому
контуру
![]() равна нулю.
равна нулю.
3) В области
![]() существует скалярная функция
существует скалярная функция
![]() ,
полный дифференциал которой совпадает
с подынтегральным выражением
,
полный дифференциал которой совпадает
с подынтегральным выражением
![]() линейного интеграла, т. е.
линейного интеграла, т. е.
![]() В этом случае функция
В этом случае функция
![]() определяется не однозначно, а с точностью
до постоянного слагаемого, т.к.
определяется не однозначно, а с точностью
до постоянного слагаемого, т.к.![]()
4) Криволинейный
интеграл потенциального векторного
поля не зависит от пути, соединяющего
две произвольные точки
![]() и
и
![]() ,
а зависит только от положения этих
точек. Имеет место формула
Ньютона-Лейбница.
,
а зависит только от положения этих
точек. Имеет место формула
Ньютона-Лейбница.
![]() , (12)
, (12)
т.е. работа в потенциальном поле не зависит от выбора пути между точками А и В, и равна разности потенциалов в этих точках.
Примеры потенциальных полей.
1. Рассмотрим поле
тяготения точечной массы m,
помещённой в начало координат О(0,0,0).
Такое поле описывается вектор-функцией
![]() ,
где γ – гравитационная постоянная,
,
где γ – гравитационная постоянная,
![]() - радиус-вектор точки
- радиус-вектор точки
![]() ,
,![]() .
С такой силой действует поле на единичную
массу, помещённую в точку
.
Поле тяготения потенциально. Его можно
представить как градиент скалярной
функции
.
С такой силой действует поле на единичную
массу, помещённую в точку
.
Поле тяготения потенциально. Его можно
представить как градиент скалярной
функции
![]() ,
называемой ньютоновским потенциалом
поля тяготения точечной массы m.
В самом деле:
,
называемой ньютоновским потенциалом
поля тяготения точечной массы m.
В самом деле:
![]()
Аналогично:
![]()
![]() Тогда
Тогда
![]()
2. Поле электрического
точечного заряда е,
помещённого
в начало координат, описывается в точке
вектором напряжённости
![]() ,
(
,
.)
Это поле потенциально. Его можно
представить как градиент скалярной
функции
,
(
,
.)
Это поле потенциально. Его можно
представить как градиент скалярной
функции
![]() ,
которая называется потенциалом
электрического поля точечного заряда
е.
,
которая называется потенциалом
электрического поля точечного заряда
е.
![]() .
.
Определение 8.
Поверхности
уровня (линии уровня для плоского поля)
потенциала
![]() называются эквипотенциальными
поверхностями (линиями).
называются эквипотенциальными
поверхностями (линиями).
Отметим, что эквипотенциальная поверхность (линия) и векторная линия, проходящие через общую точку , взаимно ортогональны в ней.
Пример 13.
Проверить,
является ли поле
![]() потенциальным. Если является, то найти
потенциал поля, построить эквипотенциальные
линии и векторные линии поля. Выделить
векторную и эквипотенциальную линии,
проходящие через точку
потенциальным. Если является, то найти
потенциал поля, построить эквипотенциальные
линии и векторные линии поля. Выделить
векторную и эквипотенциальную линии,
проходящие через точку
![]() .
.
Решение. Поле определено на всей плоскости XOY.
![]() ,
,![]() ;
;
Проверим, выполняются
ли необходимые и достаточные условия
потенциальности:
![]() ,
,
![]()
![]() поле
потенциально.
поле
потенциально.
1.Для нахождения
функции
![]() составим систему:
составим систему:
![]()
![]() .
.
Из первого уравнения, проинтегрировав его по переменной x, найдём:
![]() .(Роль
константы здесь играет любая функция,
зависящая от x).
Для отыскания
.(Роль
константы здесь играет любая функция,
зависящая от x).
Для отыскания
![]() подставим найденную функцию
во второе уравнение системы:
подставим найденную функцию
во второе уравнение системы:![]()
![]() .
Получили
.
Получили
![]() .
.
2.Условие
эквипотенциальности:
![]() ,
отсюда получаем семейство эквипотенциальных
линий
,
отсюда получаем семейство эквипотенциальных
линий
![]() .
.
Приведём уравнение к каноническому виду:
![]()
![]() .
.
Это семейство
гипербол при
![]() .
.
Если
![]() ,
получим уравнения прямых
,
получим уравнения прямых
![]() .
.
Строим эквипотенциальные линии на плоскости XOY.
3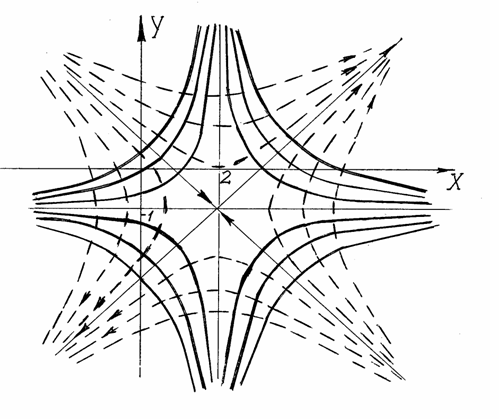 .Векторные
линии поля
.
Составим дифференциальное уравнение
векторных линий поля:
.Векторные
линии поля
.
Составим дифференциальное уравнение
векторных линий поля:
![]() .Решим
его :
.Решим
его :![]()
Рисунок 9![]()
![]() ,
и две прямые
,
и две прямые
![]() ,
если
,
если![]() .
Строим векторные линии на плоскости
XOY.
.
Строим векторные линии на плоскости
XOY.
Эквипотенциальные
и векторные линии в точках пересечения
ортогональны. Проверим это для линий,
проходящих через точку
![]() .
.
4.Подставим
координаты точки
в
уравнение векторных линий:
![]() .
Через точку М
проходит
векторная линия
.
Через точку М
проходит
векторная линия
![]() .
.
Аналогично найдём
![]() для эквипотенциальной линии, проходящей
через точку М:
для эквипотенциальной линии, проходящей
через точку М:
![]() .
Через точку М
проходит
эквипотенциальная линия
.
Через точку М
проходит
эквипотенциальная линия
![]() .
.
Вычислим угловые коэффициенты касательных к этим кривым в точке М:
Для векторной
линии:![]() в
т. М:
в
т. М:
![]() .
.
Для эквипотенциальной
линии
![]() в т. М:
в т. М:
![]() .
.
![]() - условие
перпендикулярности двух касательных.
- условие
перпендикулярности двух касательных.
Вывод: векторная и эквипотенциальная линии в точке М ортогональны.
П
Рисунок 10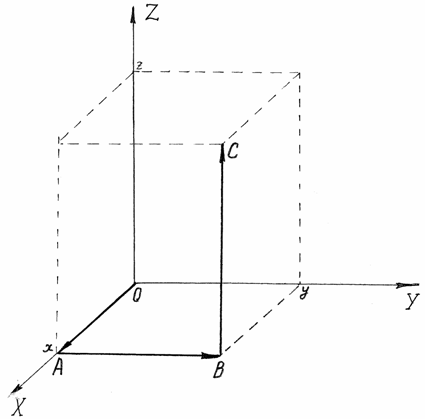 ример
14. Убедиться,
что поле
ример
14. Убедиться,
что поле
![]() является потенциальным, найти потенциал
поля
и
вычислить работу, совершаемую этим
полем при перемещении материальной
точки из
является потенциальным, найти потенциал
поля
и
вычислить работу, совершаемую этим
полем при перемещении материальной
точки из
![]() в
в
![]() .
.
Решение.
Для ответа на вопрос о потенциальности
данного поля вычислим частные производные
от функций
![]() ,
,![]() ,
,
![]() .
Эти функции непрерывны вместе со своими
частными производными в любой точке
.
Эти функции непрерывны вместе со своими
частными производными в любой точке
![]() .
.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Видим, что выполняются
необходимые и достаточные условия
потенциальности поля
:
![]() ,
,
![]() ,
,
![]() ,
ч. т. д.
,
ч. т. д.
Для вычисления
потенциала воспользуемся тем, что
линейный интеграл в таком поле не зависит
от пути интегрирования и может быть
вычислен по формуле Ньютона-Лейбница.
Пусть точка
![]() - начало пути, а некоторая точка
- начало пути, а некоторая точка
![]() - конец пути.
Вычислим
интеграл
- конец пути.
Вычислим
интеграл

 по контуру, состоящему из отрезков
прямых, параллельных координатным осям
(см.Рисунок 10).
по контуру, состоящему из отрезков
прямых, параллельных координатным осям
(см.Рисунок 10).
![]() .
.
Уравнения частей
контура:![]() ,
,
![]() ,
,![]() .
.
Тогда
![]()
![]() ,
x
здесь
зафиксирован, поэтому
,
x
здесь
зафиксирован, поэтому
![]() ,
,
![]() ,
здесь зафиксирован y,
поэтому
,
здесь зафиксирован y,
поэтому
![]() .
.
В итоге получаем:
![]() .
.
Теперь тот же
интеграл вычислим по формуле
Ньютона-Лейбница.
 =
= =
=![]()
![]() .
.
Приравняем
результаты:
![]()
![]() .
.
Из полученного
равенства следует, что
![]()
![]() ,
а
,
а
![]() Потенциал данного поля
найден.
Потенциал данного поля
найден.
Найдём работу,
совершаемую векторным полем при
перемещении точки из
в
.
В потенциальном поле работа равна
разности потенциалов в конечной и
начальной точках пути, т. е.
![]()
Пример 15. Убедиться
в потенциальности векторного поля
![]() ,
найти уравнения эквипотенциальных
поверхностей и выделить среди них ту,
которая проходит через точку M(2,1,1).
,
найти уравнения эквипотенциальных
поверхностей и выделить среди них ту,
которая проходит через точку M(2,1,1).
Решение.
Поле определено в каждой точка пространства
![]() .
Проверим потенциальность поля (см.
(11)):
.
Проверим потенциальность поля (см.
(11)):
![]() условия
выполнены, поле потенциально. Можно
найти потенциал так же, как в примере
12, а можно другим способом. Для нахождения
потенциала имеем систему:
условия
выполнены, поле потенциально. Можно
найти потенциал так же, как в примере
12, а можно другим способом. Для нахождения
потенциала имеем систему:
![]()
![]()
![]() .
.
Интегрируя первое
уравнение системы по переменной x,
найдём
![]() .
Продифференцируем полученное выражение
по y:
.
Продифференцируем полученное выражение
по y:
![]() .Из
второго уравнения системы получаем:
.Из
второго уравнения системы получаем:
![]()
![]() .Уточним
выражение для потенциала:
.Уточним
выражение для потенциала:
![]() .
Дифференцируем
по переменной z
и сравниваем
с третьим уравнением системы:
.
Дифференцируем
по переменной z
и сравниваем
с третьим уравнением системы:
![]()
![]() .
.
Восстановим всю
функцию:
![]() .
Потенциал найден.
.
Потенциал найден.
Потребовав
![]() ,
получим уравнения эквипотенциальных
поверхностей:
,
получим уравнения эквипотенциальных
поверхностей:
![]() .
.
Приведём это
уравнение к каноническому виду:
![]() .
.
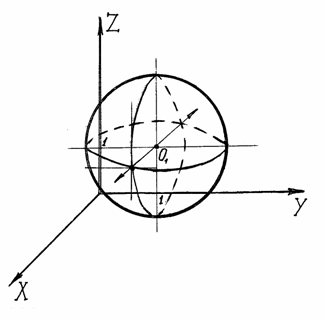
Это уравнения сфер
с центром в точке O(0;1;1)
и радиусом
![]()
Найдём эквипотенциальную
поверхность, проходящую через точку
M(2,1,1).
Подставим координаты точки в уравнение
поверхности, определим
![]() :
:
![]() через
точку М
проходит сфера
через
точку М
проходит сфера
![]() .
.
Найдём векторную линию поля, проходящую через точку М.
Уравнения векторных линий:
Рисунок 11![]()
![]() в
т. М:
в
т. М:![]() ,
т. е. через т. М
проходит прямая
,
т. е. через т. М
проходит прямая![]() .
Т.к. она проходит через центр сферы,
касательная плоскость к сфере в т. М
ей перпендикулярна. Т. е. векторная линия
и эквипотенциальная поверхность в т. М
взаимно ортогональны.
.
Т.к. она проходит через центр сферы,
касательная плоскость к сфере в т. М
ей перпендикулярна. Т. е. векторная линия
и эквипотенциальная поверхность в т. М
взаимно ортогональны.
Направление движения поля по этой линии совпадает с направлением оси OX при x>0 и противоположно ему при x<0. Это совпадает с направлением увеличения потенциала U. Действительно, чем больше потенциал, тем больше радиус сферы.
