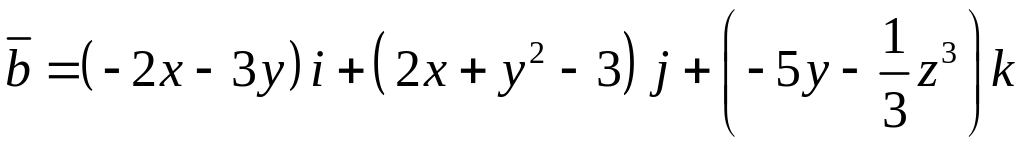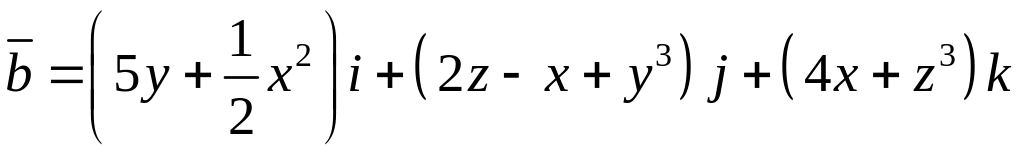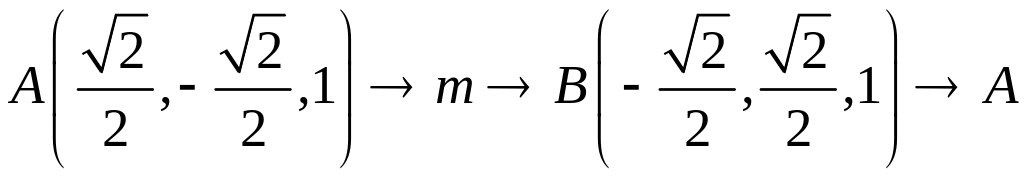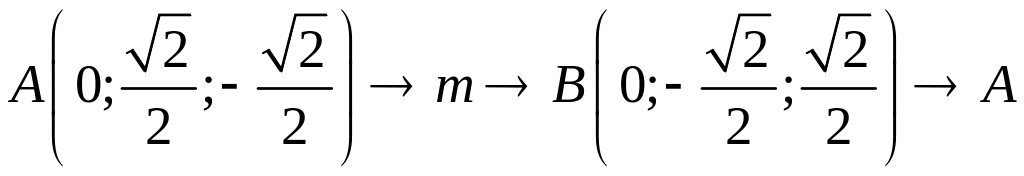- •§1. Скалярные и векторные поля.
- •§2. Поверхности и линии уровня.
- •§3. Производная по направлению скалярного поля.
- •Контрольное задание 2.
- •§4. Градиент скалярного поля.
- •Контрольное задание 3.
- •§5. Векторные линии поля.
- •Контрольное задание 4.
- •§6. Линейный интеграл векторного поля.
- •Формула Грина.
- •Контрольное задание 5.
- •§7. Потенциальное векторное поле.
- •Примеры потенциальных полей.
- •Контрольное задание 6.
- •§8. Поток векторного поля.
- •Контрольное задание 7.
- •§9. Дивергенция векторного поля. Соленоидальное векторное поле.
- •Формула Остроградского – Гаусса.
- •Контрольное задание 8.
- •§10. Ротор (вихрь) векторного поля. Формула Стокса.
- •Контрольное задание 9.
- •§11. Операторы Гамильтона и Лапласа.
- •Дифференциальные операции второго порядка.
- •Запись дифференциальных операций второго порядка в операторной форме.
- •Контрольное задание 10.
- •Ответы к контрольным заданиям.
- •Список литературы.
- •Оглавление.
- •Скалярные и векторные поля. 4
Контрольное задание 10.
Найти
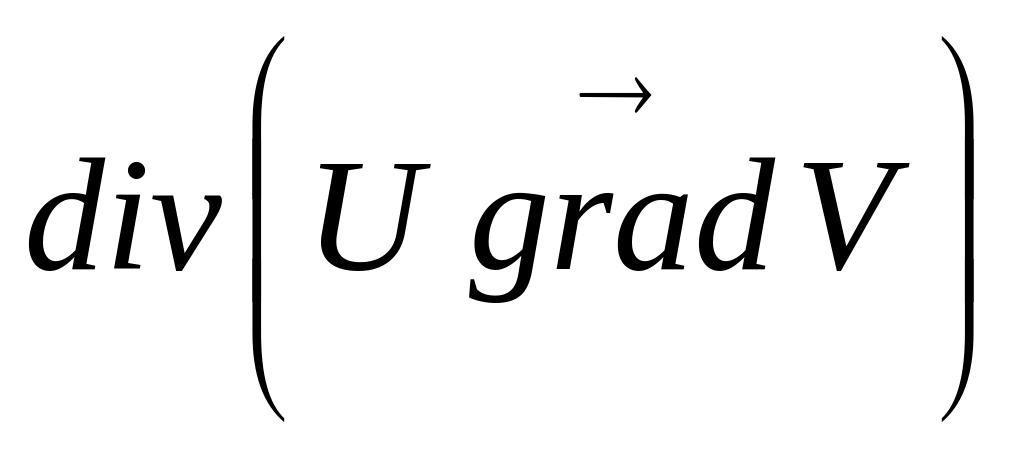 ,
,
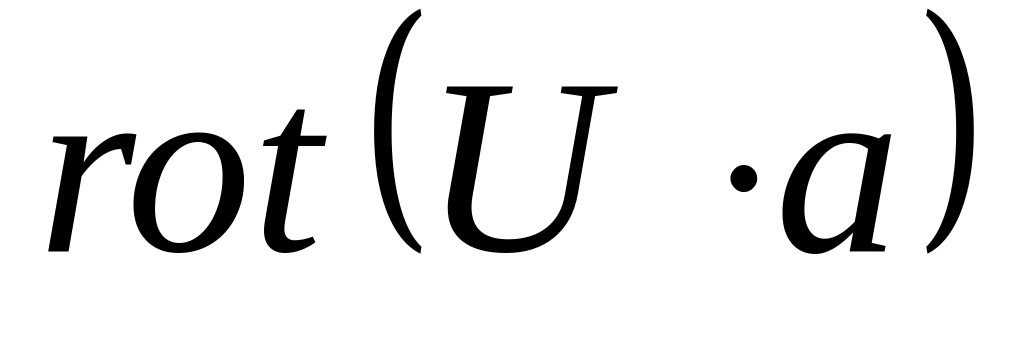 ,
,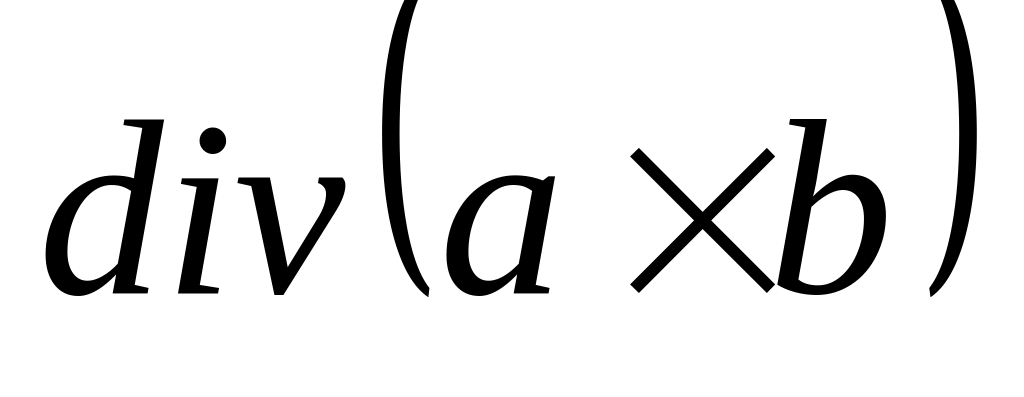 .
.Для векторного поля
 вычислить
,
вычислить
,
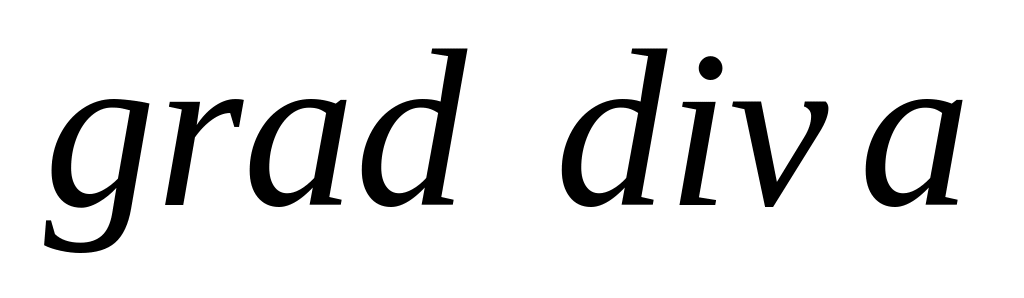 .
.
Доказать, что плоское векторное поле, потенциалом которого служит функция
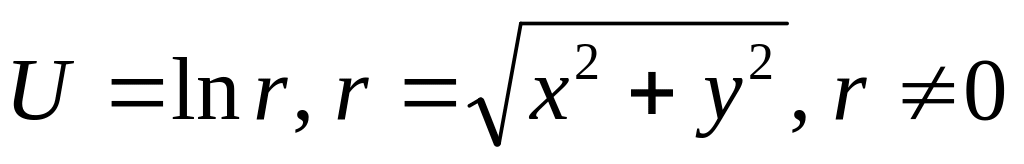 ,
гармоническое.
,
гармоническое.
Ответы к контрольным заданиям.
№1.
1) Семейство
параболоидов
![]() и ось OZ;
и ось OZ;
2) плоскость
YOZ
и
семейство
конусов
![]() ,
,![]() ;
;
3) семейство гиперб.
параболоидов
![]() ,
плоскости
,
плоскости
![]() ;
;
4) семейство эллипт.
параболоидов
![]() ;
;
5) семейство гипербол
![]() ,
оси OX
и OY.
,
оси OX
и OY.
№2.
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() .
.
№3.
1)
![]() ;
4)а) на прямой
;
4)а) на прямой
![]() ;
;
2)![]() ;
б) в
точках конуса
;
б) в
точках конуса
![]() ;
;
3)![]() ;
в) в
точке
;
в) в
точке
![]() ;
;
5)
![]() .
.
№4.
Эллипсы
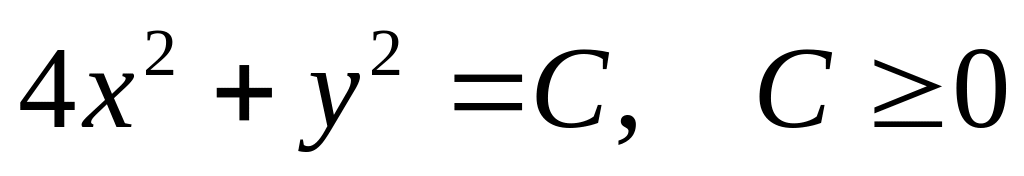 ;
2)
;
2)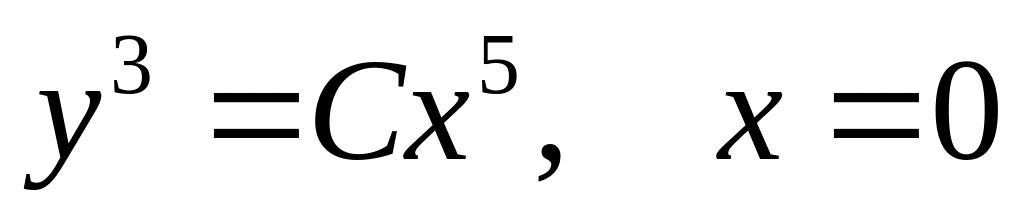 ;
;
3) Прямые линии
![]() ,
с выколотой точкой O(0,0,0).
,
с выколотой точкой O(0,0,0).
4)
![]() .
.
№5.
1)
![]() ;
2)а) 0; б) 0; 3)
;
2)а) 0; б) 0; 3)
![]() ;
4)
,
5)
;
4)
,
5)
![]() .
.
№6.
1)
![]()
![]() - линии равного потенциала,
- линии равного потенциала,
векторные линии
![]() ;
;
![]() ;через
точку A
проходит вект. линия
;через
точку A
проходит вект. линия
![]() ,эквипотенц.
линия
,эквипотенц.
линия![]()
2)
![]() ;
3)
;
3)
![]() ;
;
4)
![]() .
.
№7.
1)
![]() ;
2) а) 0; б)
;
2) а) 0; б)
![]() ;
3)
;
3)
![]() .
.
№8.
1)Поле нейтрально
на плоскости
![]() .
Над этой плоскостью – стоки поля, под
ней – источники;
.
Над этой плоскостью – стоки поля, под
ней – источники;
2)
![]() ;
3) 0; 4)
;
3) 0; 4)
![]() ;
5) а)
;
5) а)
![]() ;
б)
;
б)
![]() .
.
№9.
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() при
при
![]() ,
,
![]() ,
нет, да;
,
нет, да;
4) Ц=![]() ,
Ц
,
Ц![]() ;
6)
;
6)
![]() .
.
№10.
1)
![]() ,
,
![]() ,
,
![]() ;
;
2)
![]() ,
,
![]() .
.
Типовой расчёт. «Теория поля».
Задача 1.
Дано векторное поле
![]()
Проверить, что это поле является потенциальным.
Найти потенциал поля
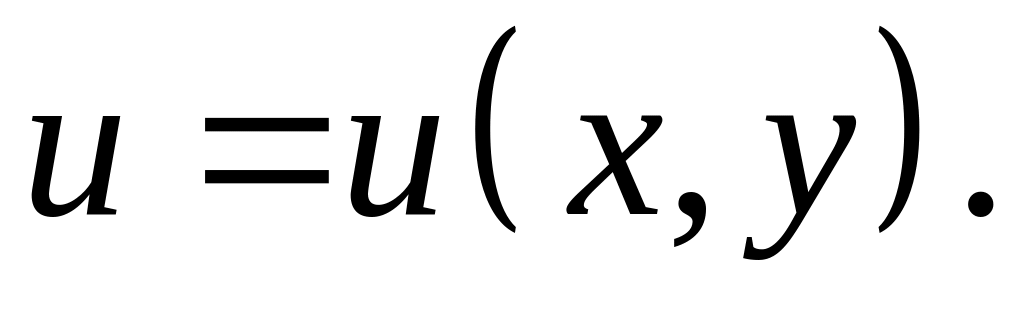
Найти уравнение линий равного потенциала и изобразить линии равного потенциала на чертеже.
Составить уравнение векторных линий поля
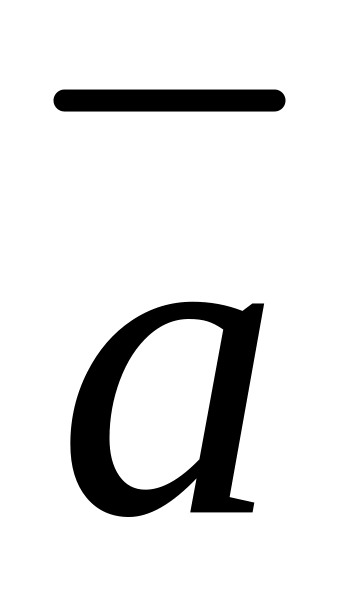 и изобразить векторные линии на том
же чертеже, указав стрелками направление
векторных линий.
и изобразить векторные линии на том
же чертеже, указав стрелками направление
векторных линий.Вычислить линейный интеграл
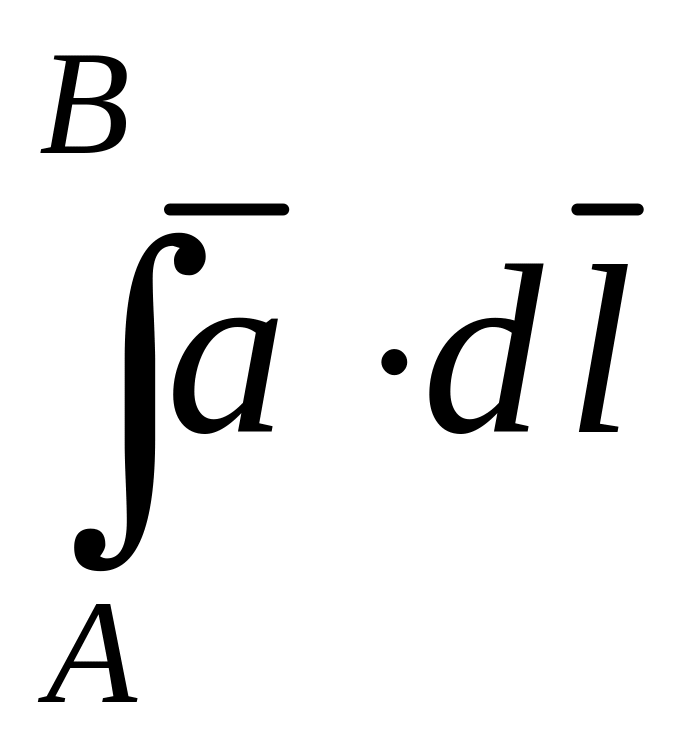 .
.
Вар. |
Векторное поле |
Точка A |
Точка B |
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
|
17 |
|
|
|
18 |
|
|
|
19 |
|
|
|
20 |
|
|
|
21 |
|
|
|
22 |
|
|
|
23 |
|
|
|
24 |
|
|
|
25 |
|
|
|
26 |
|
|
|
27 |
|
|
|
28 |
|
|
|
29 |
|
|
|
30 |
|
|
|
Задача 2.
Дано векторное поле
![]() .
.
Найти дивергенцию векторного поля
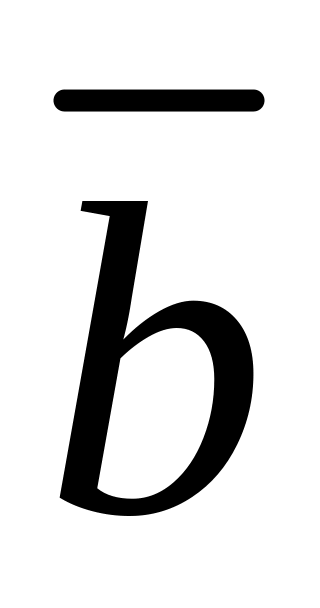 ,
исследовать расположение источников
и стоков векторных линий поля.
,
исследовать расположение источников
и стоков векторных линий поля.Найти поток векторного поля через замкнутую поверхность
 .
.Найти ротор векторного поля .
Вычислить циркуляцию поля вдоль замкнутой линии
 двумя способами: а) преобразовав
линейный интеграл в определенный с
использованием уравнений линии
;
б) преобразовав линейный интеграл в
поверхностный с помощью теоремы Стокса.
двумя способами: а) преобразовав
линейный интеграл в определенный с
использованием уравнений линии
;
б) преобразовав линейный интеграл в
поверхностный с помощью теоремы Стокса.
Выяснить, как изменится циркуляция поля вдоль контура , если изменить расположение контура в данном поле. Найти наибольшее значение циркуляции для данного контура.
Вар. |
Поле : - поверхность, ограничивающая тело Т. - замкнутая линия |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
диаметра
:
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
диаметра
|
19 |
|
20 |
|
21 |
|
22 |
|
23 |
|
24 |
|
25 |
диаметра
:
|
26 |
|
27 |
|
28 |
-
состоит из дуги окружности
двух
отрезков прямых
и
:
|
29 |
|
30 |
|

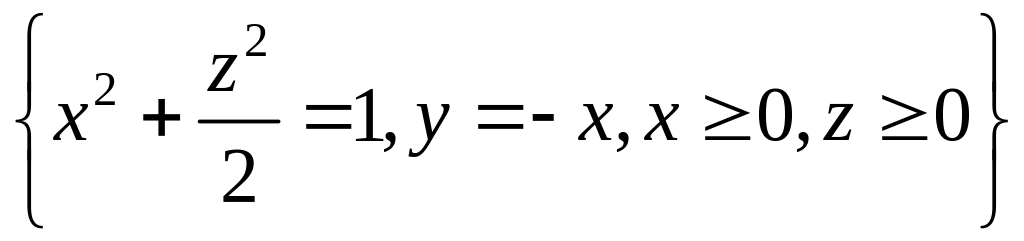 и
двух отрезков прямых
и
двух отрезков прямых