
- •Глава 8. Неявные функции. Дифференцируемые Отображения
- •8.1. Неявные функции заданные одним уравнением
- •8.2. Векторные отображения
- •В силу (13) это будет означать, что
- •Предел отображения обозначается:
- •8.3. Неявные функции n-переменных. Обратные отображения
- •8.4. Условный экстремум
- •8.5. Поверхности в трехмерном евклидовом пространстве
- •8.6. Контрольные вопросы
- •8.7. Примеры решения задач
- •8.8. Задачи для самостоятельного решения
Предел отображения обозначается:
 .
(14)
.
(14)
Очевидно,
что для любого
 справедливы неравенства
справедливы неравенства
 .
.
Тогда
ясно, что из условия (14) следует
 .
.
Определение
4. Пусть
 и является его предельной точкой.
Отображение
и является его предельной точкой.
Отображение
 называется непрерывным
в точке
называется непрерывным
в точке
 ,
если оно определено в точке
и существует предел
,
если оно определено в точке
и существует предел
 при
равный
при
равный
 ,
т.е.
,
т.е.
 .
.
Если – изолированная точка множества , то считается непрерывной в точке .
Ясно,
что отображение
непрерывно в точке
каждая функция
 непрерывна в точке
как функция n-переменных.
непрерывна в точке
как функция n-переменных.
Определение
5. Отображение
 ,
определенное на открытом множестве
называется дифференцируемым
в точке
,
определенное на открытом множестве
называется дифференцируемым
в точке
 ,
если каждая функция
,
если каждая функция
 дифференцируема в точке
.
дифференцируема в точке
.
Так
как каждая функция n-переменных
 дифференцируемая в точке
,
то ее полное приращение в этой точке
имеет вид
дифференцируемая в точке
,
то ее полное приращение в этой точке
имеет вид
 ,
,
где
 ;
;
 .
.
Эти
полные приращения
 представляют собой m
скалярных равенств, и их можно записать
в векторном виде в пространстве
представляют собой m
скалярных равенств, и их можно записать
в векторном виде в пространстве
 ,
(15)
,
(15)
где
 ,
(16)
,
(16)
 .
.
Более подробно (15) можно записать так:

 .
.
Определение
6. Векторы
(16) называют частными
производными
отображения
в точке
по переменным
 .
.
Определение
7. Отображение
 ,
линейное относительно переменных
,
линейное относительно переменных
 называют дифференциалом
отображения
в точке
и обозначают
называют дифференциалом
отображения
в точке
и обозначают
 .
(17)
.
(17)
Заметим,
что
 – дифференциал независимой переменной
– дифференциал независимой переменной
 .
Формулы (15) и (17) можно записать в матричной
форме:
.
Формулы (15) и (17) можно записать в матричной
форме:
 ,
(18)
,
(18)
где

называется матрицией Якоби, а
 ;
;
 .
.
Матрица
Якоби называется также производной
вектор-функции
в точке
,
и обозначается
 .
Заметим, что градиент функции переменных
.
Заметим, что градиент функции переменных
 есть частный случай матрицы Якоби при
,
и поэтому он также является производной
этой функции.
есть частный случай матрицы Якоби при
,
и поэтому он также является производной
этой функции.
Если , то матрица Якоби квадратная размерностью n:
 .
.
Определитель
такой матрицы Якоби называется якобианом
и обозначается
 .
.
Пример 8.
Найти дифференциал отображения
 в точке
в точке
 ,
где
,
где
 .
.
Решение.
Для функций
 ,
,
 ,
,
 найдем матрицу Якоби
найдем матрицу Якоби
 в точке
в точке
 .
Получаем
.
Получаем
 .
.
Тогда
 .
.
Пример
9. Найти
якобиан
 отображения
отображения

Решение.
 .
.
Снова
рассмотрим случай, когда
.
 – вектор-функция, определенная на
открытом множестве
.
Будем интерпретировать
как векторное поле на
.
– вектор-функция, определенная на
открытом множестве
.
Будем интерпретировать
как векторное поле на
.
Определение
8. Векторное
поле
называется потенциальным,
если существует такая дифференцируемая
функция n-переменных
 ,
что
,
что
 .
(19)
.
(19)
Функция
 называется потенциалом
векторного поля
.
В силу дифференцируемости функции
из (19) следует
называется потенциалом
векторного поля
.
В силу дифференцируемости функции
из (19) следует

или
 .
.
Таким образом, потенциал векторного поля есть функция , градиентом некоторой является функции , т.е. само векторное поле.
Из
определения следует, что потенциал
векторного поля определяется с точностью
до постоянной С.
Если
 и
и
 два потенциала векторного поля
,
то
два потенциала векторного поля
,
то
 .
.
Теорема 8.6. Для того, чтобы дифференцируемое векторное поле, определенное в , было потенциальным, необходимо выполнение следующих условий:
 .
(20)
.
(20)
Пусть
 – потенциал поля
,
тогда
– потенциал поля
,
тогда
 .
Из дифференцируемости векторного поля
следует, что
дважды дифференцируема на
.
Тогда в силу теоремы о равенстве смешанных
производных
.
Из дифференцируемости векторного поля
следует, что
дважды дифференцируема на
.
Тогда в силу теоремы о равенстве смешанных
производных
 .
■
.
■
Замечание
1. Для
векторного поля на плоскости

 условие (20) имеет вид:
условие (20) имеет вид:
 .
.
Для
векторного поля в пространстве

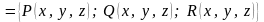 условия (20) будут иметь вид
условия (20) будут иметь вид
 .
.
Замечание 2. При некоторых предположениях относительно множества условия (20) являются и достаточными.
