5.4. Контрольные вопросы

1. Записать задачу Коши для уравнения теплопроводности в области .

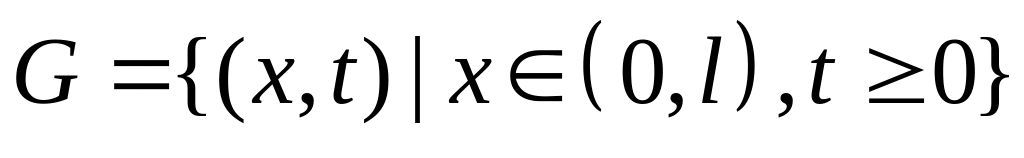2. Записать задачу Коши для уравнения колебаний в области .

3. Записать первую краевую задачу для уравнения колебаний в области .

4. Записать смешанную краевую задачу для уравнения колебаний в области .

5. Записать вторую краевую задачу для уравнения теплопроводности в области .

6. Записать краевую задачу для уравнения Пуассона в области .

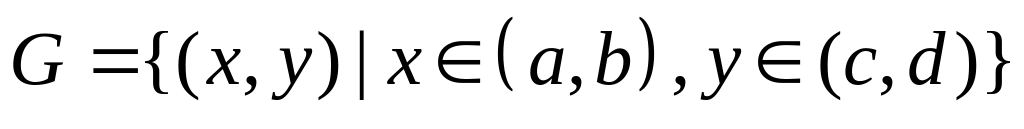7. Привести уравнение к каноническому виду в каждой из областей, где его тип сохраняется:

8. Решить задачу Штурма-Лиувилля

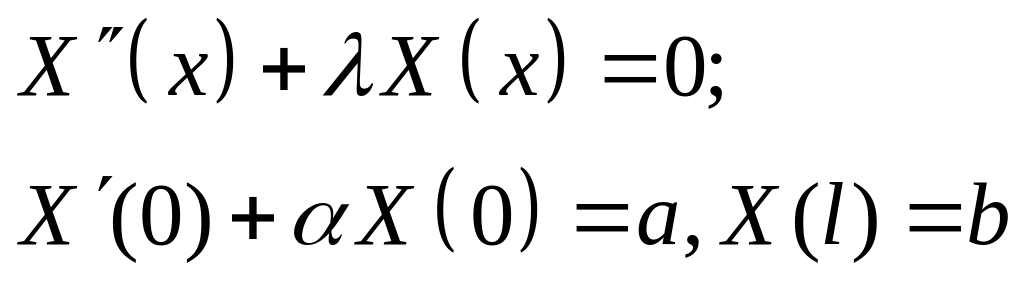
9. Решить задачу Штурма-Лиувилля

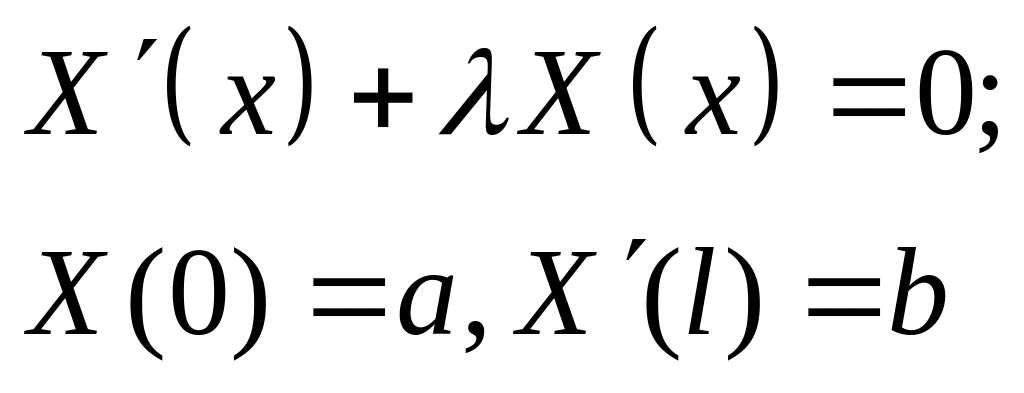
5.5. Компьютерный практикум

Пример 5.1.

Решим методом Фурье краевую задачу для неоднородного уравнения гиперболического типа

, (5.49)

, (5.50)

. (5.51)

Подберем вначале такую функцию , чтобы она удовлетворяла граничным условиям (5.51) и однородному УЧП (5.49). Пусть, например, , тогда

Тогда функция

(5.52)

удовлетворяет уравнению

(5.53)

однородным граничным условиям

(5.54)

и нулевым начальным условиям

. (5.55)

Применяя общую схему метода Фурье для решения однородного уравнения при условиях (5.54), (5.55) полагаем . Приходим к задаче Штурма-Лиувилля

Решая ее, находим собственные значения и соответствующие собственные функции

. (5.56)

Решение задачи (5.53) – (5.55) ищем в виде ряда

, (5.57)

где . (5.58)

Подставляя (5.57) в (5.53) имеем

. (5.59)

Для нахождения функций разложим функцию 5.1. в ряд Фурье по системе функций (5.56) на интервале (0, 1)

. (5.60)

Так как , то , и из (5.59) и (5.60) получаем

. (5.61)

Общее решение уравнения (5.61) будет . Используя условия (5.59), получим . Подставляя в (5.57) с учетом (5.52) находим решение исходной задачи (5.49)—(5.51):

, где .

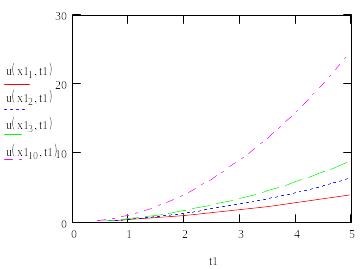
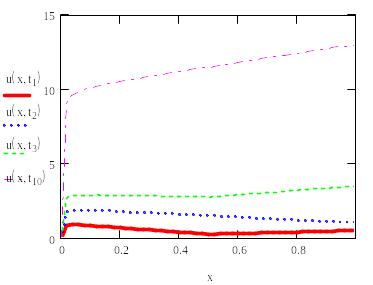
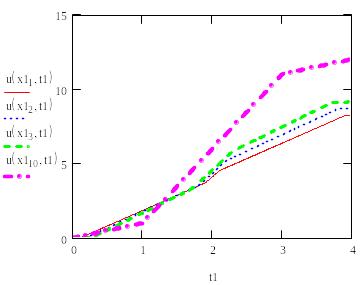
Строим график решения при различных x и в Mathcad.

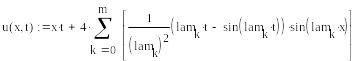
Пример 5.2.

Решим методом Фурье краевую задачу для неоднородного уравнения параболического типа.

, (5.62)

, (5.63)

. (5.64)

Подберем сначала такую функцию , чтобы она удовлетворяла граничным условиям (5.64) и начальному условию (5.63). Пусть, например, , тогда

.

Поэтому функция

(5.65)

удовлетворяет уравнению

. (5.66)

и условиям

. (5.67)

Применяя метод Фурье для решения однородного уравнения при условиях (5.67), полагаем . Приходим к задаче Штурма-Лиувилля

собственными значениями которой являются , а собственными функциями

. (5.68)

Решение задач (5.66), (5.67) ищем в виде

. (5.69)

Подставляя (6.69) в (6.66), получаем

. (6.70)

Разложим функцию в ряд Фурье по системе функций (5.68) на интервале (0, 1):

. (5.71)

Так как , то из (5.70) и (5.71) находим

(5.72)

при условии . (5.73)

Решением задач Коши (5.51), (5.52) является

. (5.74)

Из (5.65), (5.69), (5.73) находим решение исходной задачи (5.62)—(5.64):

, где .

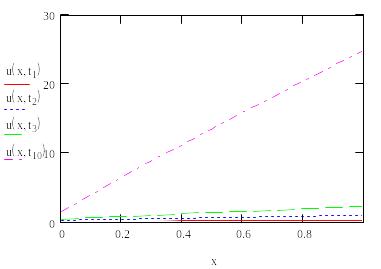
Строим график решения при различных в Mathcad.
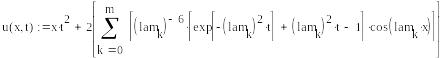