
5.3. Метод Фурье для уравнения теплопроводности
Рассмотрим общую схему метода разделения переменных (Фурье) на примере краевых задач для неоднородного уравнения теплопроводности [3].
Решение краевых задач для уравнения
теплопроводности методом Фурье.
Сформулируем задачу об отыскании
нестационарного температурного поля
![]() в тонком стержне длины
в тонком стержне длины
![]() ,
имеющем в начальный момент времени
температуру
,
если на поверхностях
,
имеющем в начальный момент времени
температуру
,
если на поверхностях
![]() и
и
![]() этого слоя происходит теплообмен с
окружающей средой, имеющей нулевую
температуру. Требуется найти решение
линейного однородного параболического
уравнения
этого слоя происходит теплообмен с
окружающей средой, имеющей нулевую
температуру. Требуется найти решение
линейного однородного параболического
уравнения
![]() (5.28)
(5.28)
удовлетворяющее при
![]() начальному условию
начальному условию
![]() (5.29)
(5.29)
и однородными граничными условиями третьего рода
![]() (5.30)
(5.30)
Следуя методу Фурье разделения переменных, нетривиальные решения уравнения (5.28), удовлетворяющие граничным условиям (5.30), будем искать в виде
![]() .
(5.31)
.
(5.31)
Подставив предполагаемую форму решения (5.31) в уравнение (5.28) и разделив переменные, получим
![]()
Поэтому функции и должны быть определены как решения дифференциальных уравнений
![]() (5.32)
(5.32)
![]() (5.33)
(5.33)
Граничные условия (5.30) с учетом (5.31) дают условия для функции в виде
![]() (5.34)
(5.34)
Задача Штурма-Лиувилля (5.33), (5.34) имеет
нетривиальные решения только при
определенных, собственных значения
![]() ,
которые можно выразить через неотрицательные
корни
,
которые можно выразить через неотрицательные
корни
![]() трансцендентного уравнения
трансцендентного уравнения
![]() ,
(5.35)
,
(5.35)
а соответствующие им собственные функции
![]() имеют вид
имеют вид
![]() .
.
Квадраты норм этих функций
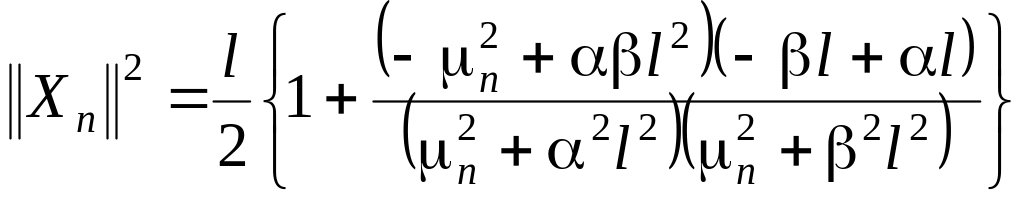 .
.
При
![]() для выражения (5.32) запишем общее решение
для выражения (5.32) запишем общее решение
![]() (5.36)
(5.36)
Подставив найденные функции и в выражение (5.31), получим частные решения уравнения (5.28), удовлетворяющие граничным условиям (5.30)
![]() .
.
Составим формально ряд, членами которого
являются функции
![]() :
:
![]() .
(5.37)
.
(5.37)
Функция удовлетворяет граничным условиям (5.30), так как этим условиям удовлетворяет каждый член ряда (5.37).
Определим коэффициенты
![]() так, чтобы выполнялось начальное условие.
Подставляя ряд (5.37) в (5.29), получаем
так, чтобы выполнялось начальное условие.
Подставляя ряд (5.37) в (5.29), получаем
![]() .
(5.38)
.
(5.38)
Это соотношение представляет собой
разложение функции
в ряд Фурье по системе ортогональных
на отрезке
![]() собственных функций
собственных функций
![]() ,
а коэффициенты
являются коэффициентами Фурье и
определяются по формуле
,
а коэффициенты
являются коэффициентами Фурье и
определяются по формуле
![]() .
(5.39)
.
(5.39)
Можно показать, что если функция
кусочно-непрерывная на отрезке
![]() ,
то ряд (5.37) с коэффициентами
,
определяемыми по формуле (5.39), удовлетворяет
уравнению (5.28) в области
,
то ряд (5.37) с коэффициентами
,
определяемыми по формуле (5.39), удовлетворяет
уравнению (5.28) в области
![]() ,
т.е. этот ряд сходится и его можно
дифференцировать почленно дважды по
и один раз по
[4].
,
т.е. этот ряд сходится и его можно
дифференцировать почленно дважды по
и один раз по
[4].
Рассмотрим задачу для неоднородного уравнения теплопроводности
![]() (5.40)
(5.40)
с начальным условием
(5.41)
и граничными условиями
![]() (5.42)
(5.42)
Решение этой задачи будем искать в виде
ряда Фурье по системе собственных
функций
![]() задачи на собственные значения (5.33),
(5.34), т.е. в форме разложения
задачи на собственные значения (5.33),
(5.34), т.е. в форме разложения
![]() .
(5.43)
.
(5.43)
считая при этом параметром.
Ряд (5.43) удовлетворяет граничным условиям
(5.42). Поэтому функции
![]() следует определить так, чтобы ряд (5.43)
удовлетворял уравнению (5.40) и начальному
условию (5.41).
следует определить так, чтобы ряд (5.43)
удовлетворял уравнению (5.40) и начальному
условию (5.41).
Учитывая полноту системы собственных
функций, представим функции
![]() и
в виде следующих рядов Фурье:
и
в виде следующих рядов Фурье:
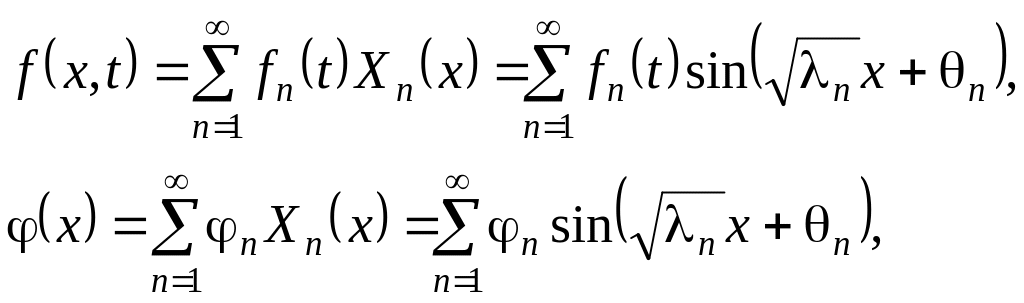 .
(5.44)
.
(5.44)
где
![]() и
и
![]() — коэффициенты Фурье, определяемые по
формулам
— коэффициенты Фурье, определяемые по
формулам
![]() (6.45)
(6.45)
![]() .
.
Подставляя предполагаемую форму решения
(5.43) и разложение (5.44) для функции
в уравнение (5.40) и заменяя при этом
![]() на
на
![]() ,
получаем
,
получаем
![]() .
.
Это соотношение, а значит, и уравнение (5.40) будут удовлетворены, если все коэффициенты разложения равны нулю, т.е.
![]() (5.46)
(5.46)
Из начального условия (5.41) с учетом (5.43) и (5.44) находим
![]() ,
,
откуда
![]() .
(5.47)
.
(5.47)
Таким образом, для нахождения искомой функции приходим к задаче Коши (5.46), (5.47) для обыкновенного линейного неоднородного дифференциального уравнения первого порядка. Решение этой задачи может быть найдено методом вариации постоянной. Оно имеет вид
![]() .
.
Подставляя функции
![]() ,
в разложение (5.43), находим решение
исходной задачи (5.40)—(5.42) в следующей
форме:
,
в разложение (5.43), находим решение
исходной задачи (5.40)—(5.42) в следующей
форме:
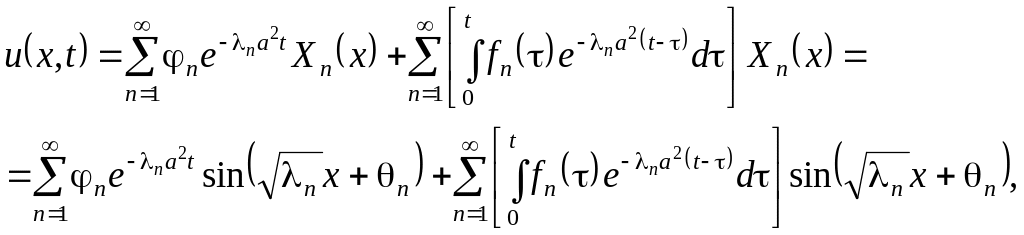 (5.48)
(5.48)
где
и
![]() определены формулами (5.45).
определены формулами (5.45).
Первое слагаемое в выражении (5.48)
представляет собой решение краевой
задачи для однородного уравнения (5.40),
когда
![]() .
.
