9. Совокупный коэффициент множественной корреляции
Это
показатель тесноты связи устанавливаемой
между результативным и 2-мя и более
факторными признаками и обозначается
как 
.
Вычисление осуществляется из соотношения:
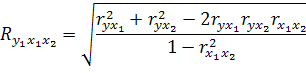
Где r – линейный коэффициент корреляции.
Изменяется от -1 до +1.
Совокупный коэффициент множественной детерминации:
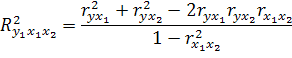
Данный совокупный коэффициент множественной детерминации показывает, какая доля вариации изучаемого показателя объясняется влиянием фактора включенного в уравнение множественной детерминации.
Общая оценка адекватности уравнения может быть получено с помощью дисперсионного F-критерия Фишера, который определяется из соотношения:
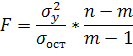
где m – число параметров уравнения регрессии
Полученное расчетное значение сравнивается с табличным, которое определяется:
Если оно окажется больше табличного значения, то уравнение регрессии статистически значимо.
Уравнение
регрессии пригодно для практического
использования в том случае если 
не менее чем в 4 раза.
Для определения значимости коэффициентов уравнения регрессии линейной используется коэффициент t – критерий Стьюдента, при n-m-1 – степень свободы.
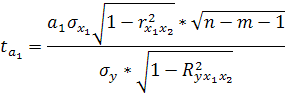
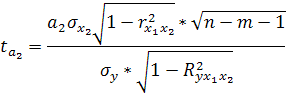
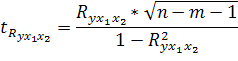
10. Экономическая интерпретация многофакторной регрессионной модели
На
основе коэффициентов регрессии нельзя
сказать какой из факторных признаков
оказывает наибольшее влияние на
результативный признак , так как
коэффициенты регрессии между собой
несопоставимы, и на их основе нельзя
оценить резерв изменения результативного
показателя. Для этого используют частные
коэффициенты эластичности Эi
и коэффициенты
.
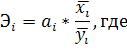
- коэффициент регрессии при i-ом
факторе;
- среднее значение i-го
фактора;
- среднее значение изучаемого показателя.
Частные коэффициенты эластичности показывают на сколько процентов в среднем изменяется анализируемый показатель с изменением на 1 процент каждого фактора при фиксируемом положении другого фактора.
Для
определения факторов в развитие которых
заложены наиболее крупные резервы,
необходимо учесть различие степени
варьирования вошедших в уравнение
факторов. Это можно сделать с помощью
- коэффициентов:
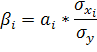
-коэффициент показывает на какую часть среднеквадратического уравнения изменяется результативный признак с изменением соответствующего фактического признака на величину его среднеквадратического отклонения.
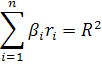
Из
соотношения можно сделать вывод, что
произведение (
)
является показателем силы влияния
соответствующего фактора на данный
показатель, причем
Получили
показатель, который называется коэффициент
и показывает какова доля вклада
анализируемого фактора в суммарном
влиянии всех отобранных факторов.
На
основе коэффициентов Э,
,
можно судить о резервах роста.
Увеличение числа существующих факторов, включаемых в модель исследуемого показателя позволяет выявить дополнительные резервы производства. Для этого используются 3-х, 4-х и так далее n-факторные регрессии.
Для решения множественной регрессии используется система нормальных уравнений вида:
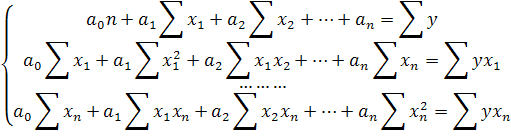
Использование многофакторного корреляционно-регрессионного анализа в экономико-статистических исследованиях:
Для приближенной оценки фактических и заданных уровней.
В качестве укрупненного норматива.
Для выявления резервов производства.
Для проведения межзаводского сравнительного анализа и выявление на его основе скрытых возможностей предприятий.
Для краткосрочного прогнозирования развития производства.