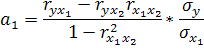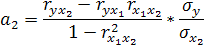4. Проверка адекватности регрессионной модели
Для
этого определяется значимость
коэффициентов простой линейной регрессии
(для совокупности в которой n
30).
Значимость определяется с помощью t-критерия Стьюдента:
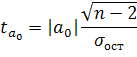
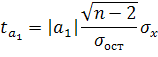
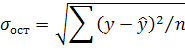
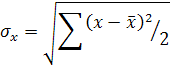
Где
– среднеквадратическое отклонение
результативного признака от выровненного
значения;
-
среднеквадратическое отклонение
факторного признака от общей средней;
n- объем выборки.
Вычисление
значения
сравниваются
с табличными значениями, причем
будут
значимыми если выполняется соотношение
>
.
Поверка адекватности модели может быть выявлена с помощью корреляционного анализа. Для этого определяется теснота взаимосвязи с помощью эмпирического корреляционного отношения:
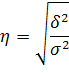
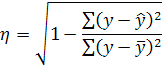
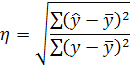
Кроме того, тесноту связи можно определить с помощью линейного коэффициента корреляции:
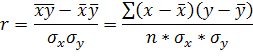
Для
малой выборки n
можно
использовать:
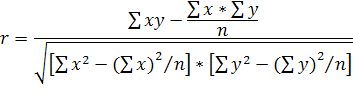
Чем ближе коэффициент корреляции к 1, тем теснее связь.
При
коэффициенте корреляции r
=
связь
является функциональной.
При
связь
обратная.
При r=0, то линейная связь отсутствует.
Для оценки значимости коэффициента корреляции r используется t-критерий Стьюдента:
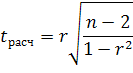
Где
n-2
- число степеней свободы при вероятности
и n
числе выборки.
Полученное значение сравнивается с табличным.
Если
,
то данный коэффициент корреляции
считается значимым.
5. Экономическая интерпретация параметров регрессии
Для интерпретации коэффициента а1 используется коэффициент эластичности. Он показывает среднее изменение результативного признака при изменении факторного признака на 1 процент и вычисляется по формуле:
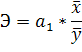
Кроме
того, вычисляются остатки 
характеризующие отклонение i-ых
наблюдений от значений, которых следуют
ожидать в среднем.
6. Многофакторный корреляционный и регрессионный анализ
Многофакторный корреляционный и регрессионный анализ позволяет оценить меру влияния на исследуемый результативный показатель каждого включенного в модель фактора при фиксированном положении остальных факторов, а также при любых возможных сочетаниях факторов с определенной степенью точности найти теоретическое значение этого показателя.
Задачей корреляционно – регрессионного анализа является построение уравнения множественной регрессии и нахождения его неизвестных параметров (a0,a1), которые находятся методом наименьших квадратов.
Пример: построение и статистический анализ двухфакторной линейной модели.
Для нахождения коэффициентов строится система уравнений:
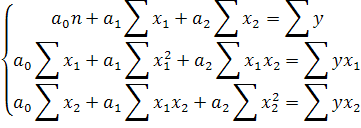
7. Парные коэффициенты корреляции
Они применяются для измерения тесноты связи между двумя из рассматриваемых переменных. Их можно рассчитать по формулам:
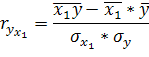
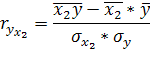
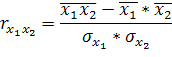
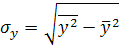
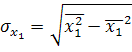
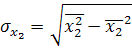
8. Частные коэффициенты корреляции
На практике все переменные, как правило, взаимосвязаны. Теснота этой связи определяется частными коэффициентами корреляции, которые характеризуют степень и влияние одного из аргументов на функцию при условии, что остальные, независимые переменные, закреплены на постоянном уровне.
Коэффициенты частной корреляции могут быть различных порядков: 1-го порядка – между признаками x1, y1, при исключении влияния признака х2.
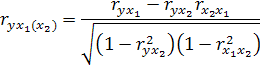
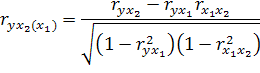
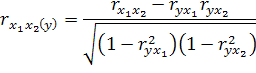
На основании парных коэффициентов корреляции и среднеквадратических отклонений можно выделить коэффициенты уравнения регрессии:
