11.3. Перенос молекул (атомов) через мембраны. Уравнение Фика

Важным элементом функционирования мембран является их способность пропускать или не пропускать молекулы (атомы) и ионы. Существенно, что вероятность такого проникновения час­тиц зависит как от направления их перемещения, например в клетку или из клетки, так и от разновидности молекул и ионов.

Эти вопросы рассматриваются в разделе физики, относящемся к явлениям переноса. Таким термином называют необратимые процессы, в результате которых в физической системе происхо­дит пространственное перемещение (перенос) массы, импульса, энергии, заряда или какой-либо другой физической величины.

К явлениям переноса относят диффузию (перенос массы вещест­ва), вязкость (перенос импульса), теплопроводность (перенос энер­гии), электропроводность (перенос электрического заряда). Здесь и в следующих параграфах рассматриваются наиболее существенные для биологических мембран явления: перенос вещества и перенос заряда. Как синоним переноса частиц в биофизике широкое распро­странение получил также термин транспорт частиц.

Выведем основное уравнение диффузии (уравнение Фика), рассматривая процесс переноса в жидкостях.

П усть через некоторую площадку S (рис. 11.10) во всех направ­лениях перемещаются молекулы жидкости. Учитывая теорию молекулярного строения жидкости, можно сказать, что молекулы пересекают площадку, перескакивая из одного положе­ния равновесия в другое.

На расстояниях, равных среднему перемещению  молекул (сред­нее расстояние между молекулами жидкости), вправо и влево от площадки построим прямоугольные параллелепипеды небольшой толщины l(l<< ). Объем каждого параллелепипеда равен Sl. Если п — концентрация молекул, то внутри выделенных параллелепипедов имеет­ся Sln молекул. Предположим, что кон­центрация молекул изменяется в про­странстве, в левом (1) выделенном па­раллелепипеде концентрация равна п₁, а в правом (2) — п₂. Следовательно, в одном параллелепипеде Sln_l молекул, а в другом — Sln₂ молекул.

Все молекулы вследствие хаотичного их движения можно ус­ловно представить шестью группами, каждая из которых пере­мещается вдоль или против направления одной из осей коор­динат. Отсюда следует, что в направлении, перпендикулярном площадке S, вдоль оси ОХ от первого параллелепипеда переска­кивает ¹/₆ Sln_l молекул, а противоположно оси ОХ от второго па­раллелепипеда перескакивает ^l/₆ Sln₂ молекул.

Время t< «пролета» этими молекулами площадки S может быть найдено следующим образом. Предположим, что все молеку­лы из выделенных объемов движутся с одинаковыми средними скоростями <>. Тогда молекулы в объеме 1 или 2, дошедшие до площадки S, пересекают ее в течение промежутка времени

t = l/<>. (11.1)

Подставляя в (11.1) выражение для средней скорости <> = ,

получаем

(11.2)

где  — среднее время «оседлой жизни» молекулы, оно может рассматриваться как среднее время перескока. «Баланс» переноса молекул через площадку S за промежуток времени t равен

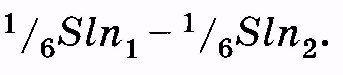(11.3)

Умножая (11.3) на массу т отдельной молекулы и деля на t, находим массовый поток сквозь площадку S:

(11.4)

т. е. масса вещества, которая за 1 с переносится через площадку S. Изменение концентрации п₂ - n_l молекул можно представить как произведение dn/dx на расстояние 2 между выделенными объ­емами:

(11.5)

В уравнении (11.4) заменим t согласно (11.2) и (п₂ – п₁) со­гласно (11.5):

(11.6)

Отношение потока к площади S, через которую он перено­сится, называется плотностью потока:

(11.7)

Произведение массы молекулы на их концентрацию есть плот­ность вещества (парциальная плотность):

(11.8)

Учитывая это, имеем из (11.7)

Это есть уравнение диффузии (уравнение Фика), которое обычно записывают в виде:

(11.9)

Знак «-» показывает, что суммарная плотность потока вещества при диффузии направлена в сторону уменьшения плотности (в сторону, противоположную градиенту плотности), D — коэффи­циент диффузии, применительно к рассмотренному примеру диффузии в жидкости он равен

(11.10)

Как видно из (11.10), единица измерения коэффициента диффу­зии [м²/с].

У равнение диффузии можно записать не только для плотности массового потока но и для плотности потока частиц и плотности потока вещества при этом в уравнении(11.9) вместо градиента плотности следует использовать соответственно градиент концентрации или градиент молярной концентрации :

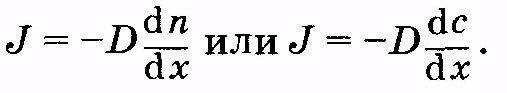(11.11)

А. Эйнштейн показал, что коэффициент диффузии пропорци­онален температуре:

(11.12)

И поэтому вместо (11.11) имеем

(11.13)

В формуле (11.12) и далее и_т — подвижность диффундирующих молекул (частиц), выраженная для моля. Вообще говоря, подвиж­ностью диффундирующей частицы (молекулы, атома, иона, электрона) и называют коэффициент пропорциональности между скоростью  частицы и силой f, двигающей частицу, в том случае, когда на частицу не действуют другие силы (например, трение или соударение с другими частицами) и она перемещается равномерно:

 = uf или и = /f. (11.14)

Как видно из (11.14), единица подвижности 1 м/(с • Н). Величины и_т и и связаны через постоянную Авогадро:

и = и_mN_A. (11.15)

Преобразуем уравнение (11.9) применительно к биологической мембране. Будем считать, что концентрация частиц, диффунди­рующих через мембрану, изменяется в мембране по линейному закону (рис. 11.11). Молярные концентрации частиц внутри и вне клетки соответственно равны c_i и с₀. Молярная концентрация этих же частиц в мембране изменяется от внутренней к наружной ее части соответственно от с_мi до с_м0. Учитывая линейное измене­ние концентрации молекул, запишем

(11.16)

где l — толщина мембраны, тогда вместо (11.11) имеем

(11.17)

Практически доступнее определить молярные концентрации час­тиц не внутри мембраны (с_мi и с_м0), а вне мембраны: в клетке (c_i) и снаружи клетки (с₀). Считают, что отношение граничных значений концентраций в мембране равно отно­шению концентраций в прилегающих к мембране слоях: с_м0/ с_мi = c₀/ c_i; откуда

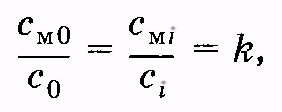(11.18)

где k — коэффициент распределения вещества (частиц) между мембраной и окружающей средой (обычно водная фаза). Из (11.18) следует

(11.19)

Подставляя (11.19) в (11.17), имеем

Пусть

Р = Dk/l, (11.20)

где Р — коэффициент проницаемости. В результате получаем уравнение для плотности потока вещества при диффузии через биологическую мембрану:

J = P(с_i - c₀). (11.21)