
- •Утверждено
- •1. Теоретические сведения
- •1.1. Электрическое поле. Напряженность
- •1.2.Принцип суперпозиции электрических полей
- •1.3.Потенциальный характер электростатического поля. Работа сил поля при перемещении зарядов. Циркуляция и ротор вектора напряженности
- •1.4.Потенциал. Потенциальная энергия заряда в электростатическом поле
- •1.5.Связь между напряженностью и потенциалом
- •1.6. Эквипотенциальные поверхности
- •2. Описание методики эксперимента
- •2.1. Аналогия между электростатическим полем и током в сплошной среде
- •3. Описание лабораторной установки вариант а
- •В ариант б
- •4. Порядок выполнения работы вариант а
- •Вариант б
- •5. Содержание отчёта
- •6. Приложение электрическое поле для изучаемых наборов электродов
- •7. Контрольные вопросы и задания
3. Описание лабораторной установки вариант а
В данной лабораторной работе аналогия между электростатическим полем и током в сплошной среде используется для исследования поля при различных формах электродов, помещённых в проводящую среду (влажный песок). К электродам подводится напряжение от звукового генератора, разность потенциалов между точками поля измеряется с помощью электронного осциллографа с двумя щупами.
Сначала для каждого из наборов электродов «плоскость - плоскость» , «плоскость - цилиндр», «цилиндр - цилиндр» строятся линии равного потенциала на поверхности песка, затем картина переносится на бумагу и дополняется линиями напряженности которые проводятся ортогонально к линиям равного потенциала.
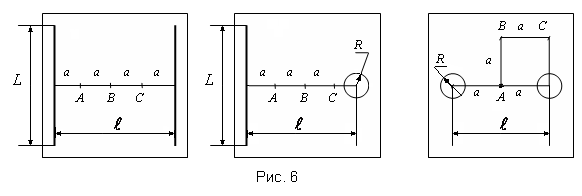
С помощью осциллографа измеряется разность потенциалов U между электродами. Затем в указанных для каждой пары электродов точках А, В, С (рис. 6) измеряется напряжённость поля. Для этого электроды устанавливаются вдоль одной силовой линии на расстоянии 1 см друг от друга, измеряется разность потенциалов и рассчитывается величина напряжённости по формуле
|E|=∆φ/∆х.
 Измеренные
значения напряжённости сравниваются
с теоретическими, которые рассчитаны
при следующих значениях:
Измеренные
значения напряжённости сравниваются
с теоретическими, которые рассчитаны
при следующих значениях:
длина плоского электрода L=248 мм,
радиус цилиндрического электрода R=24,5 мм.
Для набора «плоскость - плоскость»:
возьмём
для простоты
 =L,
тогда из формулы (П.1), которая представлена
в Приложении, получаем для точек А
и С,
полагая х=
/4,
=L,
тогда из формулы (П.1), которая представлена
в Приложении, получаем для точек А
и С,
полагая х=
/4,
ЕА=Ес= (3.1)
(3.1)
а для точки В, полагая х= /2,
Ев=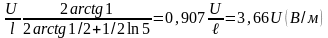 (3.2)
(3.2)
Для набора «плоскость - цилиндр» при =L из формулы Приложения (П.2) получаем значения напряжённости в точках А, В, С (х= /4, /2, 3 /4):
ЕА=0,898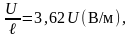 (3.3)
(3.3)
ЕВ=0,904 (3.4)
(3.4)
ЕС=1,310 (3.5)
(3.5)
Для набора «цилиндр - цилиндр» получаем из формулы Приложения (П.3) значения величины напряжённости поля при = 220 мм:
ЕА(х=0,
у=0)=0,963 (3.6)
(3.6)
ЕВ
(х=0,
у=
/2)=0,481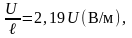 (3.7)
(3.7)
ЕС(х=у=
/2)=0,431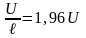
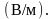 (3.8)
(3.8)
В ариант б
В качестве сплошной среды используется проводящая металлическая пластина 1, (рис.7 и 8) , покрытая парафинированным эбонитовым диэлектриком. Отверстия в диэлектрике составляют множество точек 2, используемых для исследования поля. Эксперимент проводят с двумя вариантами пластин. В первом варианте в пластину вмонтированы электроды 3 в виде параллельных плоскостей, во втором – в виде цилиндров. Электроды подключают к источнику питания 4 и создают разность потенциалов между ними 4В. Щупы 5 соединены с цифровым вольтметром 6.
Поиск линии равного потенциала проводят следующим образом. Помещают щуп 5 в любую точку исследуемого поля 1. Перемещая второй щуп в разные точки поля, отмечают точки, для которых показания вольтметра соответствуют нулю ( в трех значащих разрядах). Через эти точки проводят линии равного потенциала.
Для
двух соседних линий равного потенциала
определяют напряженность поля. Для
этого помещают первый щуп в любую точку
одной линии, второй – в ближайшую точку
второй линии. По вольтметру определяют
разность потенциалов между этими
точками, а по числу дискретов – расстояние
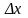 .
По формуле
.
По формуле
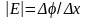

рассчитывают напряженность поля.
