
- •Утверждено
- •1. Теоретические сведения
- •1.1. Электрическое поле. Напряженность
- •1.2.Принцип суперпозиции электрических полей
- •1.3.Потенциальный характер электростатического поля. Работа сил поля при перемещении зарядов. Циркуляция и ротор вектора напряженности
- •1.4.Потенциал. Потенциальная энергия заряда в электростатическом поле
- •1.5.Связь между напряженностью и потенциалом
- •1.6. Эквипотенциальные поверхности
- •2. Описание методики эксперимента
- •2.1. Аналогия между электростатическим полем и током в сплошной среде
- •3. Описание лабораторной установки вариант а
- •В ариант б
- •4. Порядок выполнения работы вариант а
- •Вариант б
- •5. Содержание отчёта
- •6. Приложение электрическое поле для изучаемых наборов электродов
- •7. Контрольные вопросы и задания
1.2.Принцип суперпозиции электрических полей
Основная задача электростатики заключается в том, чтобы найти величину и направление вектора напряженности в каждой точке поля по заданному распределению в пространстве и величине электрических зарядов.
Рассмотрим
поле, созданное системой точечных
зарядов
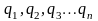 .
В механике рассматривался принцип
независимости действия сил. Согласно
этому принципу, результирующая сила
.
В механике рассматривался принцип
независимости действия сил. Согласно
этому принципу, результирующая сила
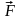 ,
действующая со стороны исследуемого
поля на пробный заряд
,
равна векторной сумме сил
,
действующая со стороны исследуемого
поля на пробный заряд
,
равна векторной сумме сил
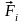 ,
приложенных к нему со стороны каждого
из зарядов
,
приложенных к нему со стороны каждого
из зарядов
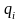 ,
,
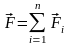 ,
(1.1)
,
(1.1)
но
известно , что
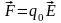 ;
и
;
и
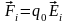 ,
где
-
напряженность результирующего поля;
,
где
-
напряженность результирующего поля;
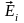 - напряженность поля, создаваемого одним
зарядом
.
- напряженность поля, создаваемого одним
зарядом
.
Тогда
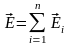 (выражение (1.1) разделили на
)
- напряженность электрического поля
системы точечных зарядов равна векторной
сумме напряженностей полей, создаваемых
каждым из этих зарядов в отдельности.
(выражение (1.1) разделили на
)
- напряженность электрического поля
системы точечных зарядов равна векторной
сумме напряженностей полей, создаваемых
каждым из этих зарядов в отдельности.
Таким образом, результирующее поле можно найти простым наложением (суперпозицией) полей отдельных зарядов. В этом и состоит принцип суперпозиции полей, или принцип независимых действий электрических полей.
Пусть
 - радиус-вектор, проведенный из точечного
заряда
в исследуемую точку поля. Тогда
напряженность, создаваемая этим зарядом
в данной точке поля
- радиус-вектор, проведенный из точечного
заряда
в исследуемую точку поля. Тогда
напряженность, создаваемая этим зарядом
в данной точке поля
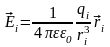 ,
а результирующая напряженность
,
а результирующая напряженность
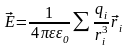 .
.
Каждое
протяженное заряженное тело можно
разбить на столь малые части, что каждая
из них будет представлять собой точечный
заряд
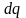 .
Поэтому формула эта пригодна для расчета
любых электрических полей.
.
Поэтому формула эта пригодна для расчета
любых электрических полей.
1.3.Потенциальный характер электростатического поля. Работа сил поля при перемещении зарядов. Циркуляция и ротор вектора напряженности
Работа,
совершаемая силами электростатического
поля при перемещении заряда
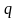 на отрезок
на отрезок
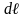 равна:
равна:

Работа по перемещению единичного положительного заряда :

Работа,
совершаемая при перемещении единичного
положительного заряда по конечному
пути
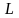 ,
определяется интегралом:
,
определяется интегралом:
 .
(1.2)
.
(1.2)
Здесь - сила Кулона, которая является центральной силой. Из механики известно, что поле центральных сил консервативно. Следовательно, работа электростатического поля по перемещению заряда не зависит от траектории, а определяется только начальной и конечной ее точками. Работа по замкнутому пути равна нулю. Поле, обладающее такими свойствами, называется потенциальным. Тогда из (1.2) имеем:
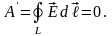 (1.3)
(1.3)
Интеграл
по замкнутому контуру
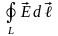 называется циркуляцией вектора
напряженности по этому контуру. Выражение
(1.3) представляет собой теорему о
циркуляции вектора
-
в электростатическом поле циркуляция
вектора напряженности
по замкнутому пути равна нулю.
называется циркуляцией вектора
напряженности по этому контуру. Выражение
(1.3) представляет собой теорему о
циркуляции вектора
-
в электростатическом поле циркуляция
вектора напряженности
по замкнутому пути равна нулю.
 Докажем
потенциальный характер электростатического
поля. Рассмотрим сначала работу
электрических сил в поле элементарного
точечного заряда
.
Работа этих сил при бесконечно малом
перемещении
Докажем
потенциальный характер электростатического
поля. Рассмотрим сначала работу
электрических сил в поле элементарного
точечного заряда
.
Работа этих сил при бесконечно малом
перемещении
 пробного единичного положительного
заряда равна:
пробного единичного положительного
заряда равна:
 ,
,
где
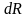 - проекция перемещения пробного заряда
- проекция перемещения пробного заряда
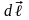 на радиус-вектор
на радиус-вектор
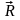 ,
проведенный из возбуждающего поле
заряда
.
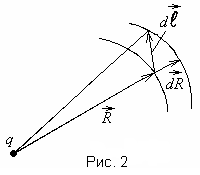
Из рис. 2 видно, что
,
проведенный из возбуждающего поле
заряда
.
Из рис. 2 видно, что
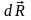 - это
приращение численного значения
радиус-вектора
,
то есть увеличение расстояния пробного
заряда
от заряда
.
Поэтому работа
- это
приращение численного значения
радиус-вектора
,
то есть увеличение расстояния пробного
заряда
от заряда
.
Поэтому работа
 может быть представлена как полный
дифференциал скалярной функции
может быть представлена как полный
дифференциал скалярной функции
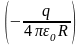 :
:
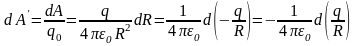 ,
,
где
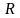 - модуль радиус-вектора
.
Тогда работа по перемещению единичного
положительного заряда из точки
- модуль радиус-вектора
.
Тогда работа по перемещению единичного
положительного заряда из точки
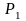 в точку
в точку
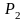 по конечному пути
:
по конечному пути
:
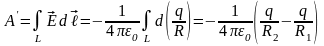 ,
,
где
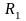 и
и
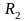 - расстояния начальной и конечной точек
пути от заряда
.
Таким образом, работа электрических
сил на произвольном пути в поле
неподвижного
- расстояния начальной и конечной точек
пути от заряда
.
Таким образом, работа электрических
сил на произвольном пути в поле
неподвижного
э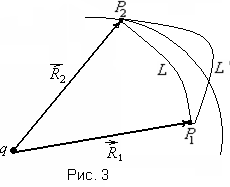 лементарного
точечного заряда действительно зависит
от положений начальной и конечной точек
этого пути и не зависит от формы пути,
и поле неподвижного точечного заряда
есть поле потенциальное.
На рис.3
работа на пути
равна работе на пути
лементарного
точечного заряда действительно зависит
от положений начальной и конечной точек
этого пути и не зависит от формы пути,
и поле неподвижного точечного заряда
есть поле потенциальное.
На рис.3
работа на пути
равна работе на пути
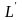 .
.
Очевидно, сумма потенциальных полей тоже есть потенциальное поле (так как если работа слагаемых сил не зависит от формы пути, то и работа равнодействующей от нее не зависит). Поле произвольной системы зарядов можно рассматривать как сумму полей каждого из точечных зарядов, поэтому всякое электростатическое поле есть поле потенциальное.
