3.11 Рівняння Бернуллі для несталого та відносного рухів рідини

Розглянуті раніше рівняння Бернуллі виводилися для випадків, коли рух рідини сталий і на кожній елементарний об’єм рідини діють лише сила тиску і сила тяжіння. Для отримання рівнянь із закону механіки враховувалася лише робота цих двох сил. Але бувають випадки, коли на рідину крім сили тяжіння і сили тиску діють інші масові сили - сила та сила інерції в абсолютному ( ) або відносному ( ) русі, і дію цих сил необхідно враховувати. Наприклад, під час відкриття засувки або коли трубопровід, по якому рухається рідина, змінює своє положення в просторі. Тоді при виводі рівняння Бернуллі враховують роботу сил інерції:

Для визначення роботи сил інерції проаналізуємо характер сили інерції і визначимо прискорення рідкої частинки.

Із загальної механіки відомо, що прискорення . Для рідкої частинки швидкість ; до того координати теж є функціями часу: .

Тоді проекції вектора прискорення можна записати так:

Тут - субстанціональні похідні від проекцій вектора швидкості за часом;

- локальні прискорення в точці простору;

, , - проекції вектора швидкості в даній точці простору.

Позначимо

; ; .

Тоді

В кожному рівнянні позначимо локальні прискорення в точці простору:

При сталому русі швидкості рідких частинок у точках простору не змінюються і локальні прискорення відсутні ( ).

Частини рівняння, що залишаються без локальних прискорень, мають назву конвективних прискорень і характеризують зміну вектора швидкості при переході від однієї точки поля до іншої. Тому:

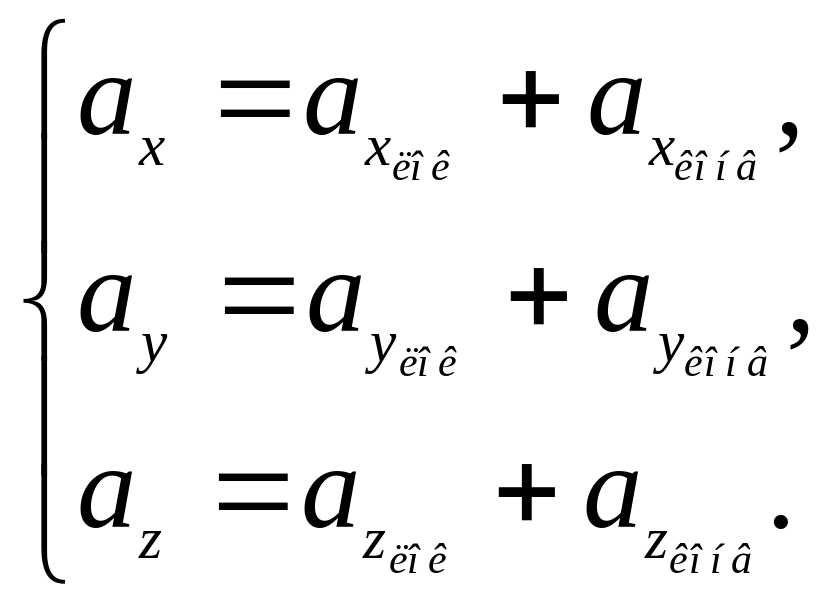
В загальному випадку прискорення рідкої частинки є сумою локального і конвективного прискорення:

. (3.33)

При несталому і відносному русі на кожну частинку рідини діють багато сил інерції – від локального прискорення і від конвективного прискорення. Тому рівняння Бернуллі для реальної рідини у випадку несталого і відносного руху матиме вигляд

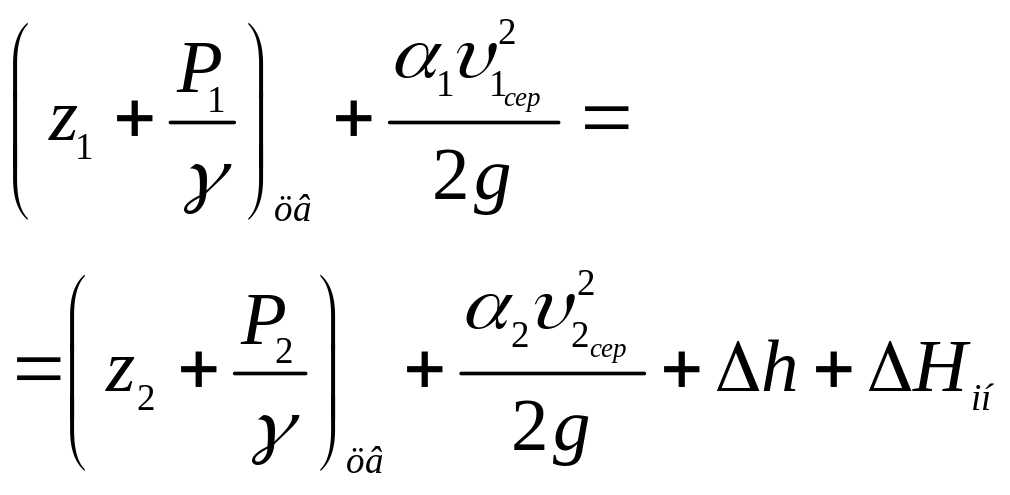, (3.34)

де - інерційний напір, який представляє роботу сили інерції, віднесену до одиниці ваги.

Розглянемо визначення величини інерційного напору для деяких характерних випадків:

а) прямолінійний рівноприскорений рух каналу.

Якщо канал з потоком рідини рухається прямолінійно з прискоренням , на всі частини рідини, що рухається по каналу, діє постійна за часом сила інерції (рисунок 3.22).

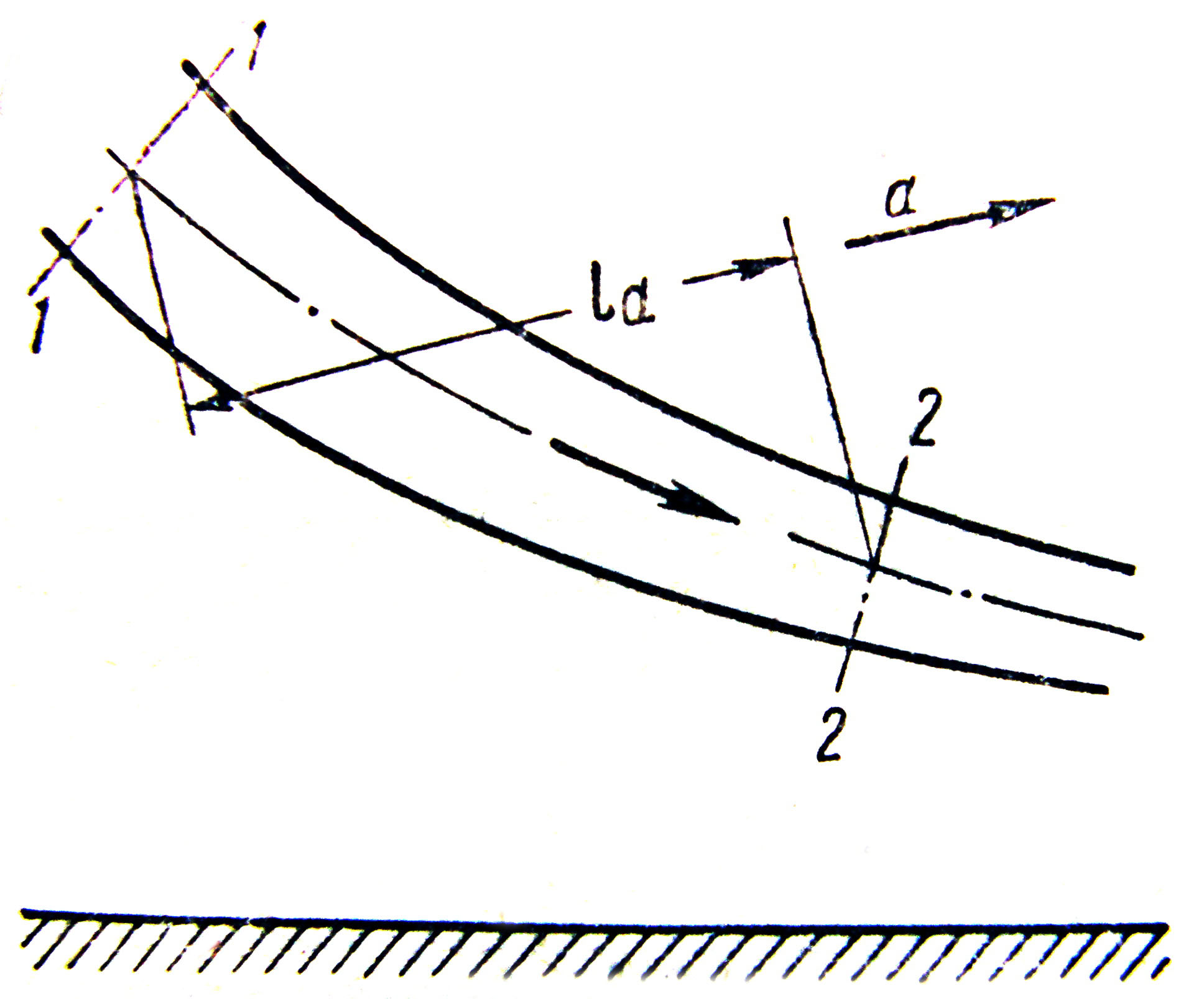
Рисунок 3.22

Якщо поділити силу інерції на вагу , отримаємо силу інерції, що діє на кожну одиницю ваги рідини

.

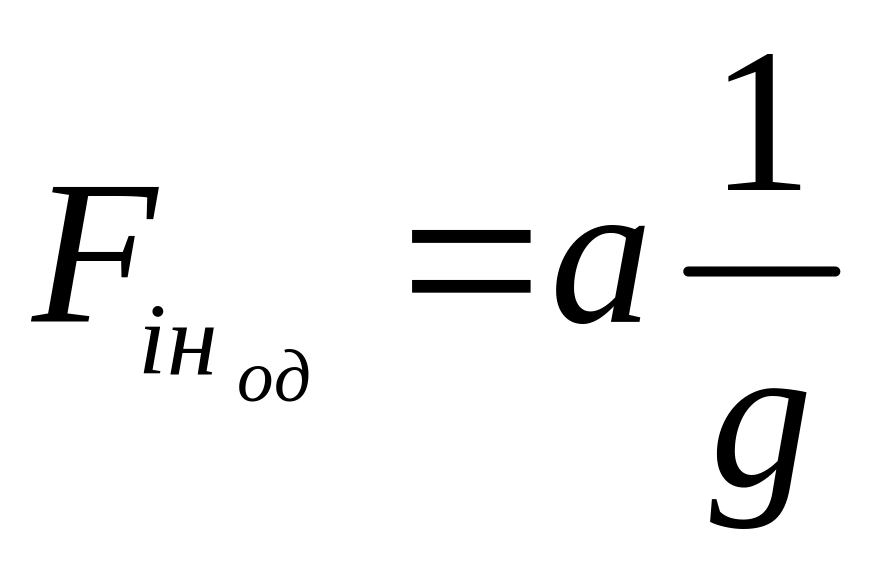Робота цієї сили по переміщенню рідини від перерізу 1 до перерізу 2 (див. рис. 3.22) визначається як добуток сили і переміщення . Тому

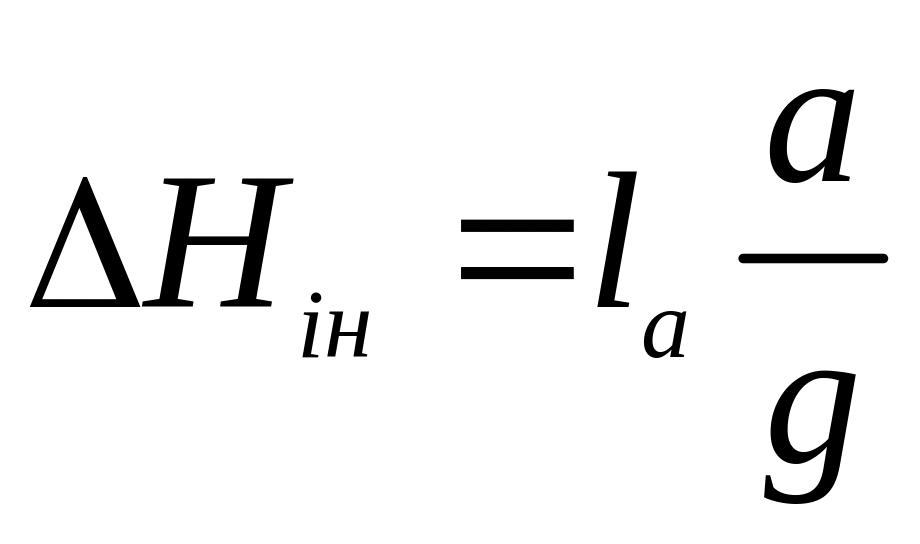, (3.35)

де - проекція відрізку каналу на напрям прискорення .

Величину в правої частині рівняння (3.34) підставляють зі знаком плюс, якщо прискорення напрямлено від перерізу 1 до перерізу 2, внаслідок зменшення тиску в другом перерізі відносно першого (сила інерції має напрямок від перерізу 2 до перерізу 1, тому інерційний напір аналогічний гідравлічним втратам).

Якщо прискорення напрямлено від перерізу 2 до перерізу 1, тоді інерційна сила має напрямок від перерізу 1 до перерізу 2 і допомагає течії. В цьому випадку інерційний напір повинен мати знак мінус в правої частині рівнянні (3.34), тому що він збільшує тиск в перерізі 2, тобто зменшує гідравлічні втрати напору;

б) рідина рухається в каналі, що обертається із постійною кутовою швидкістю .

В цьому випадку на рідину діє сила інерції обертового руху (рисунок 3.23).

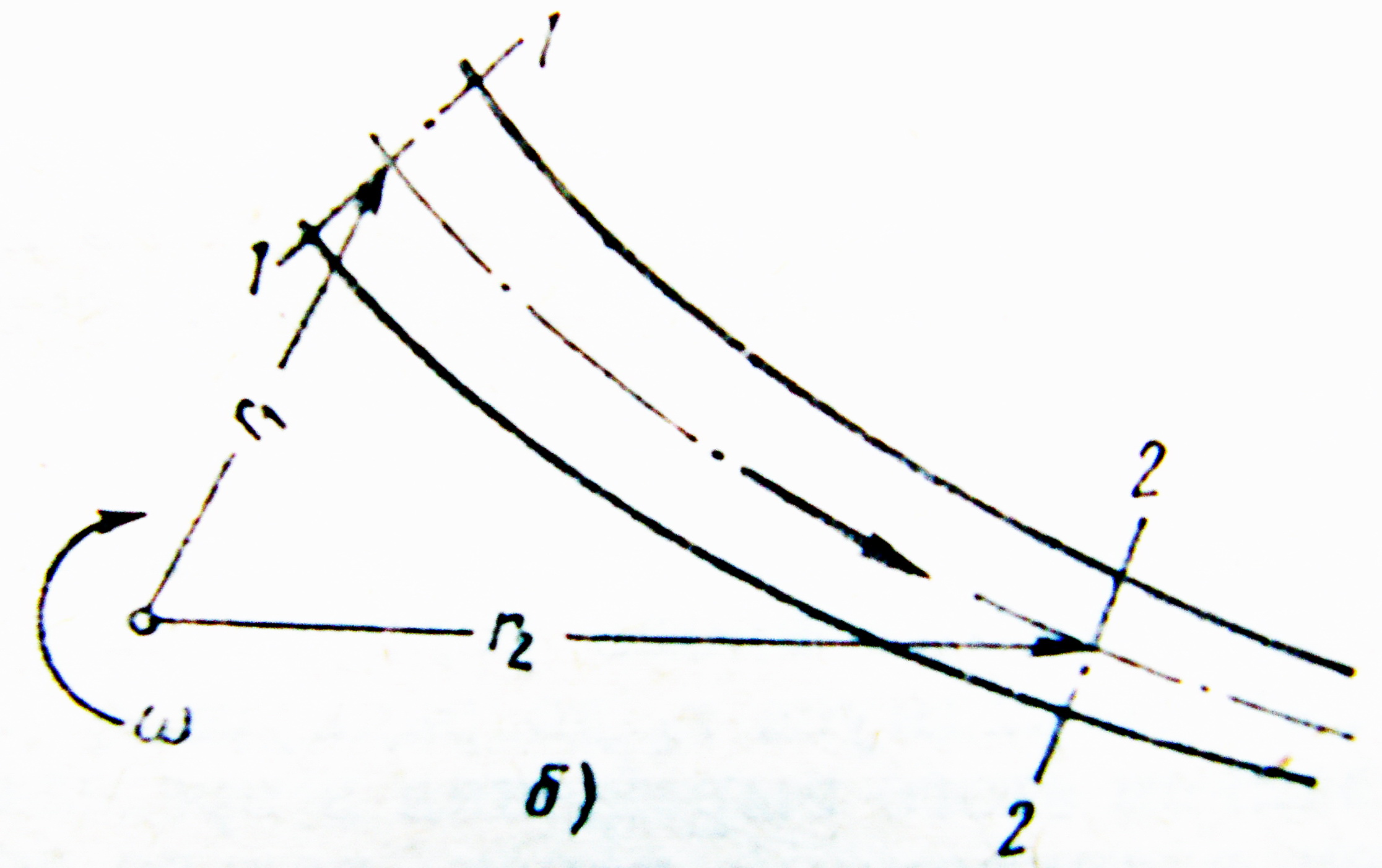
Рисунок 3.23

Тоді на одиницю ваги рідини в цьому випадку буде діяти сила інерції . Робота цієї сили при переміщенні уздовж радіусу на відстань буде рівною 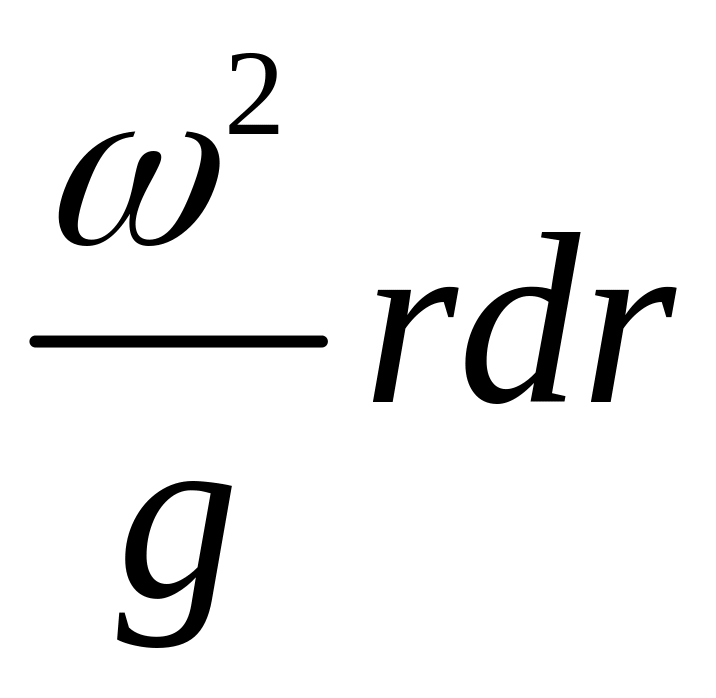. Виконав інтегрування, знайдемо величину інерційного напору при переміщенні рідини на відстань від до :

. (3.36)

Знак в формулі (3.36) визначають за правилом, розглянутим для випадку прямолінійного рівноприскореного руху каналу;

в) відносний рух рідини.

При відносному русі слід враховувати коріолісову силу інерції .

Інерційний напір в цьому випадку знаходять за формулою

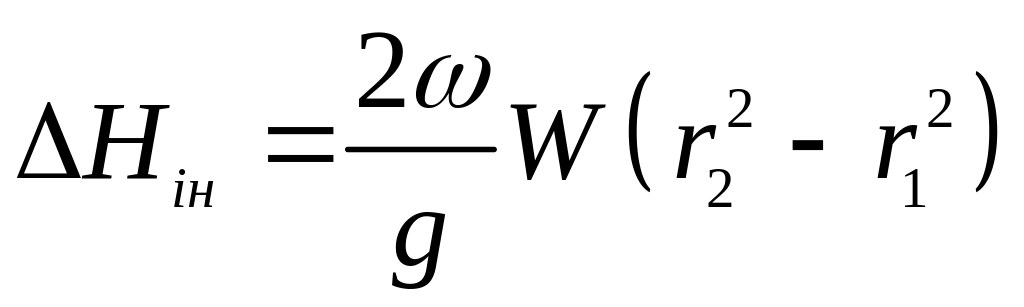. (3.37)