3.9.2 Зміна енергії вздовж трубопроводу для потоку в’язкої рідини

Для потоку в’язкої рідини зміна енергії вздовж трубопроводу буде відрізнятися відносно потоку ідеальної рідини.

На рисунку 3.21 представлено графічну ілюстрацію зміни енергії для трубопроводу з рисунку 3.20 у випадку потоку реальної рідини.

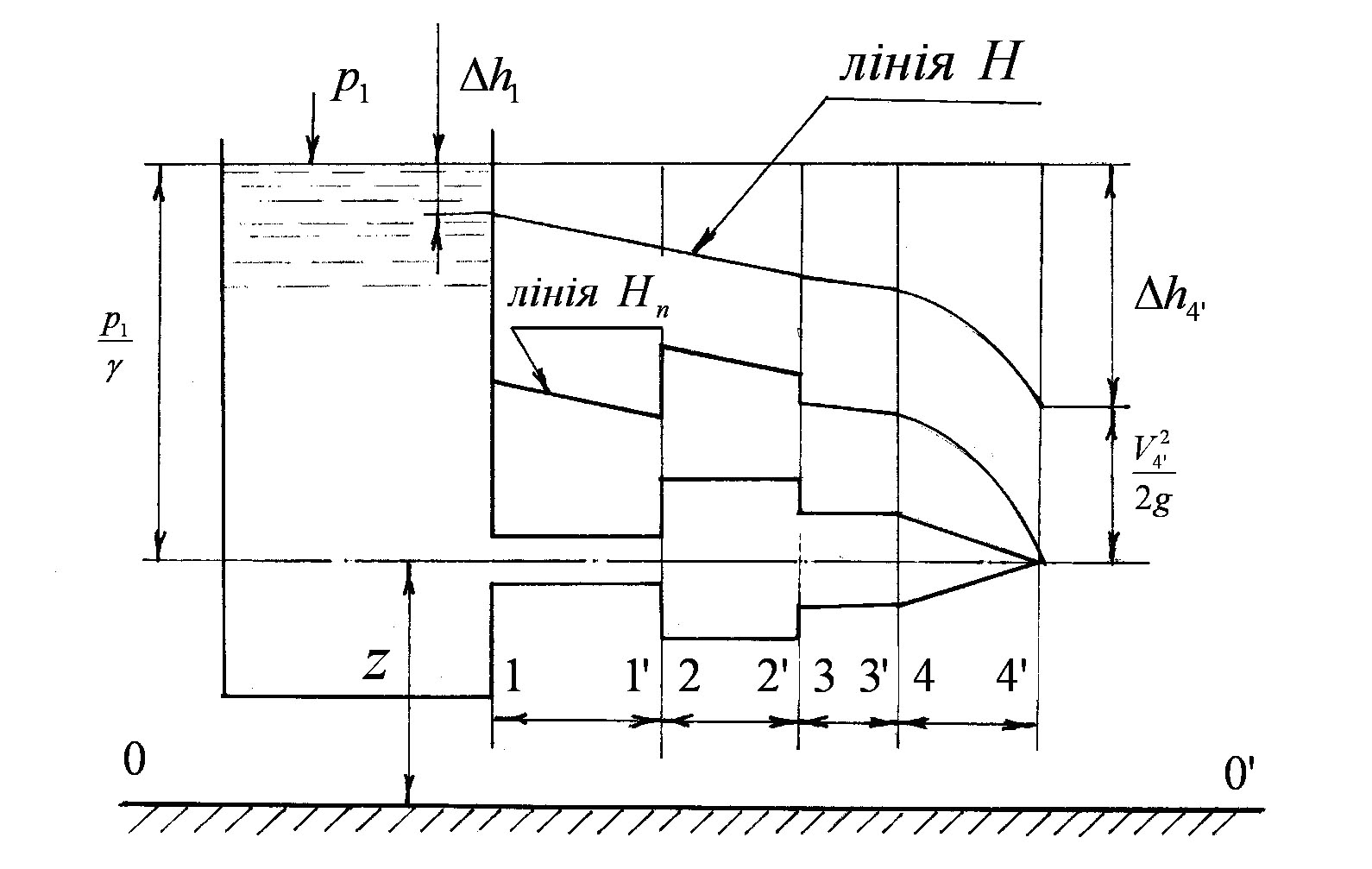
Рисунок 3.21

Якщо рідина реальна (в’язка), рівняння Бернуллі для двох перерізів матиме вигляд

.

Аналізуючи характер зміни енергії в цьому випадку, слід зауважити:

а) лінії повного напору і п’єзометричного напору мають похил відносно площини порівняння (горизонтальної площини);

б) під час руху рідини вздовж ділянки трубопроводу постійного діаметра (за умовою незмінного розподілу швидкості) зміна повного і п’єзометричного напорів характеризується паралельними лініями внаслідок того, що гідравлічний і п’єзометричний похили однакові.

3.10 Рівняння Бернуллі для стисливої рідини

При невеликих змінах тиску вздовж потоку рівняння Бернуллі можна використовувати для газового потоку (стисливої рідини) у раніше отриманому вигляді для нестисливої рідини:

. (3.28)

В цьому випадку вираз (3.28) – це питома енергія одиниці ваги газу.

Якщо кожний член рівняння (3.28) помножити на , здобудемо рівняння для енергії одиниці маси рідини

. (3.29)

При значних змінах тиску змінюється і густина ( ), тому у цьому випадку слід використовувати рівняння (3.29) для одиниці маси (за умовою виконання )

При великих тисках величиною енергії положення можна знехтувати, тому що вона достатньо мала у порівнянні з іншими видами енергії. Тому рівняння (3.29) запишемо у вигляді

,

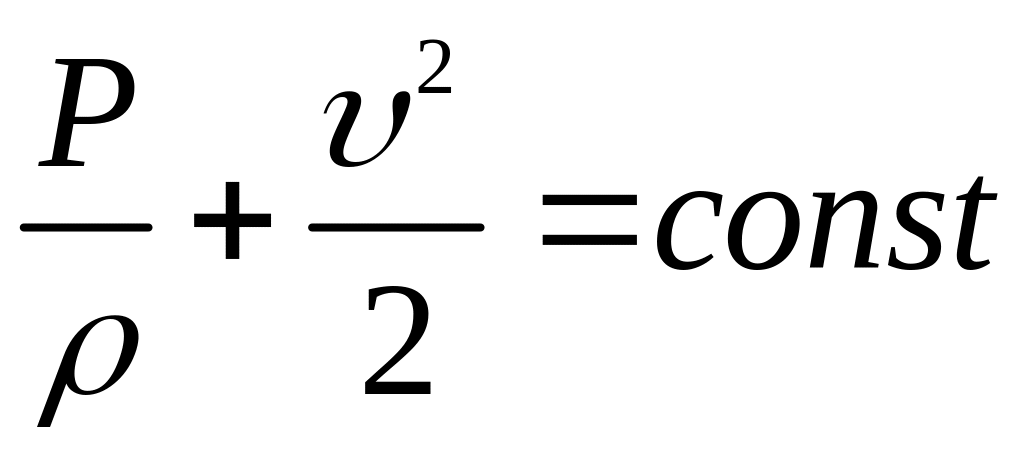або в диференційної формі

.

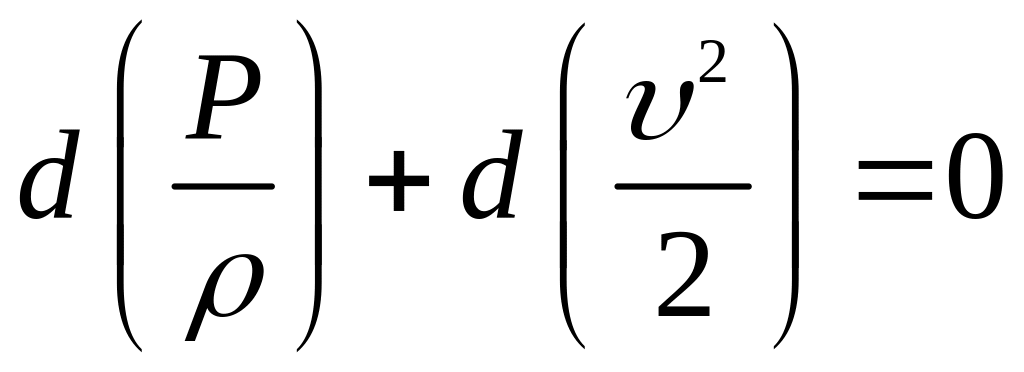Інтегруючи цей вираз уздовж елементарної струминки, дістаємо

. (3.30)

Вираз (3.30) є рівняння Бернуллі для стисливої рідини (газу).

З енергетичної точки зору член рівняння є питома потенціальна енергія газу з урахуванням перетворення його внутрішньої енергії (при зміні тиску об’єм газу змінюється і виділяється теплова енергія). Тому енергетичний зміст рівняння (3.30) можна сформулювати так: при усталеній течії газу вздовж трубки течії сума питомої потенціальної і кінетичної енергії є величиною сталою.

Для того, щоб скористатися рівнянням (3.30), слід знати залежність . Тобто потрібно знати характеристику процесу зміни стану газу в розглядуваному випадку течії.

Якщо газ тече без теплообміну із навколишньою атмосферою, то такий процес у загальному випадку називають адіабатичним. Якщо при цьому знехтувати в’язкістю (тобто газ ідеальний), то процес буде називатися ізоентропічним.

Для ізоентропічного процесу виконується залежність

,

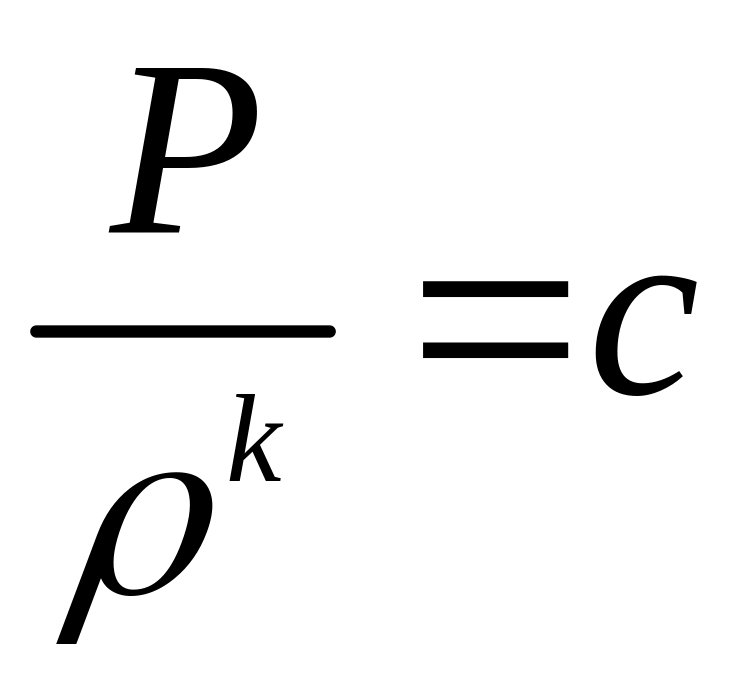де - показник адіабати процесу (для повітря );

– стале число.

Тобто

.

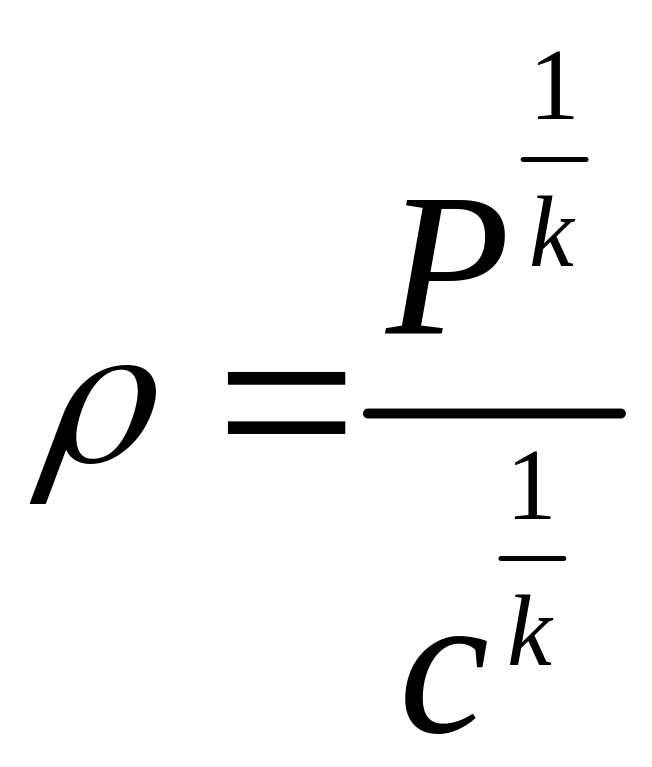Тоді

.

Виконаємо заміну:

.

Тоді

.

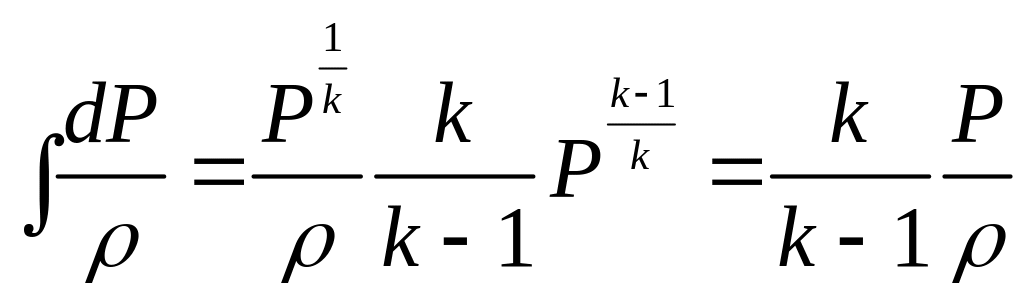Тепер рівняння (3.30) матиме вигляд

. (3.31)

Враховуючи рівняння газового стану Клайперона-Менделєєва ( ), рівняння (3.31) можна записати у вигляді

, (3.32)

де - універсальна газова константа;

- температура.

Із рівняння (3.32) випливає, що зміна швидкості вздовж струминки газу пов’язана зі зміною температури. Тобто при збільшенні температури швидкість падає, а при зменшенні температури швидкість зростає. Це використовують для збільшення швидкості потоку в ракетних двигунах.