3.8 Рівняння Бернуллі для потоку реальної рідини

При русі в’язкої (реальної) рідини частина механічної енергії потоку втрачається на подолання сили опору між живими перерізами. Природу цього опору і визначення його розміру розглянемо пізніше, а зараз будемо стверджувати, що при русі в’язкої рідини від перерізу 1-1 до перерізу 2-2 механічна енергія буде зменшуватися, тобто Е₁  Е₂ (або Н₁  Н₂). З урахуванням цього

 .

Щоб скласти рівняння, слід додати до правої частини величину втраченої питомої енергії . Тоді рівняння Бернуллі для потоку реальної (в’язкої) рідини можна записати у вигляді

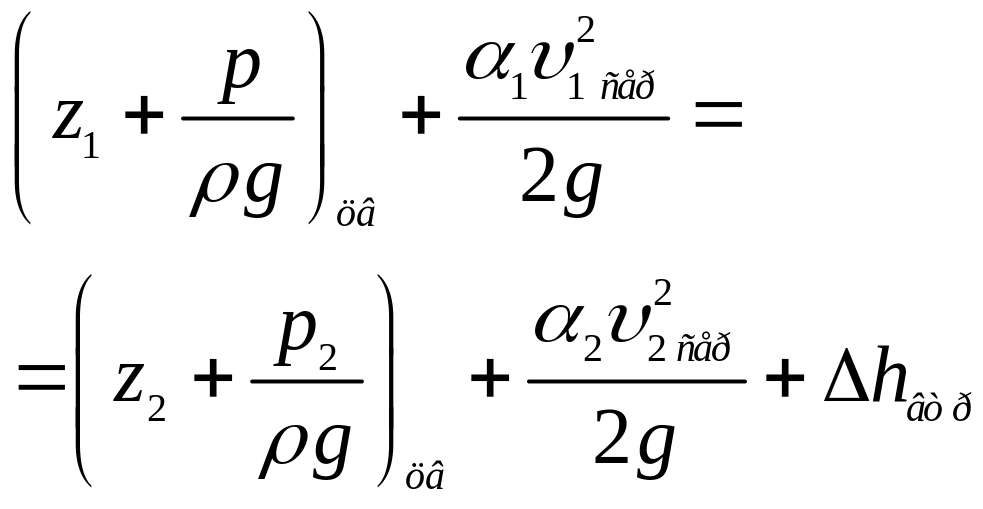. (3.24)

З енергетичної точки зору рівняння (3.24) виражає явище розсіювання (дисипації) енергії. Інакше кажучи, при русі частина механічної енергії рідини внаслідок в’язкості переходить необоротно в теплову форму енергії, тобто для потоку втрачається.

Геометричну інтерпретацію рівняння Бернуллі для потоку реальної (в’язкої) рідини подано на рисунку 3.19.

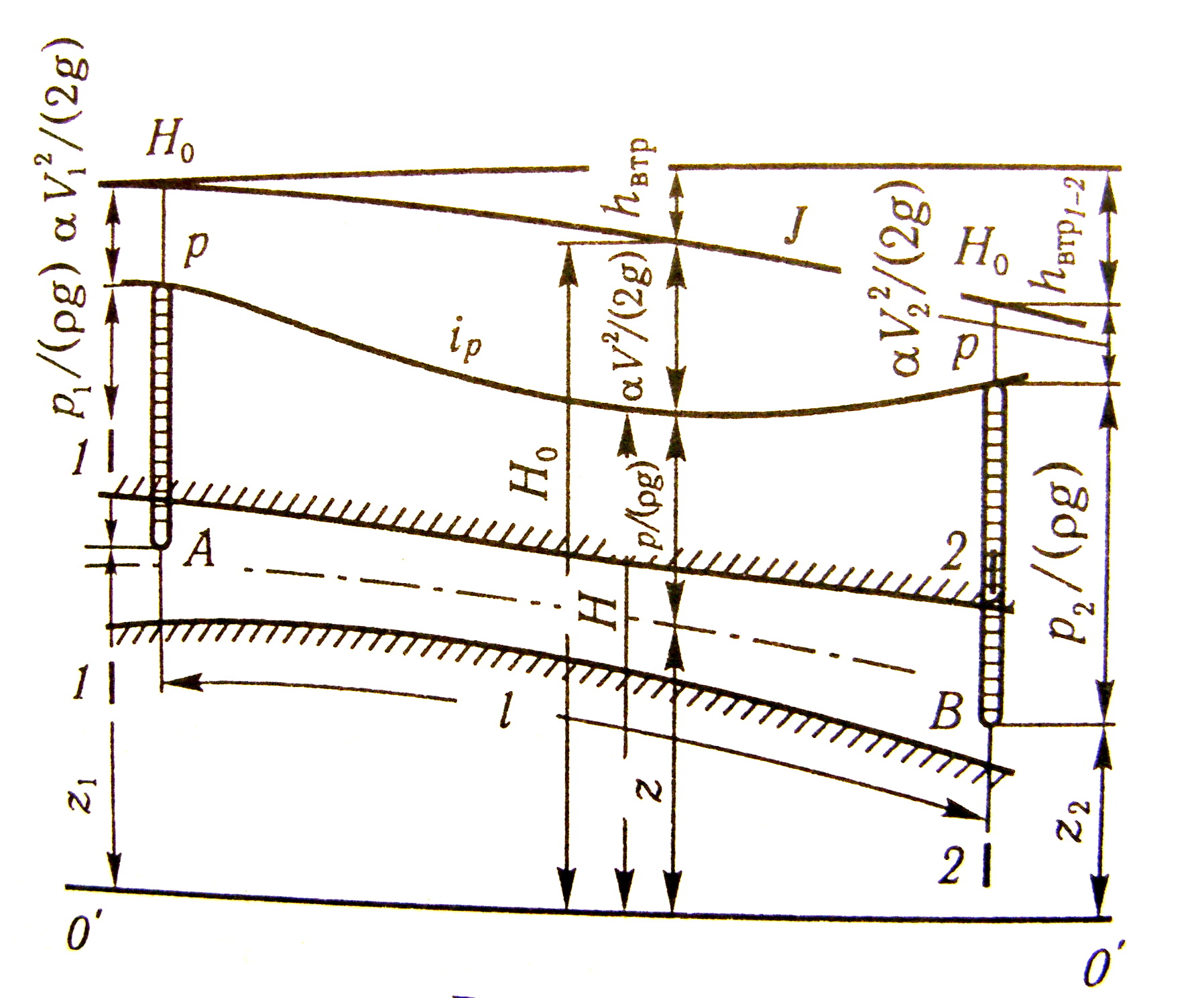
Рисунок 3.19

З геометричної точки зору рівняння Бернуллі є сумою трьох лінійних величин , , . Точки А і В, яки розміщені в перерізах 1-1 і 2-2, мають відмітки і над горизонтальною площиною порівняння 0 - 0. П’єзометричні висоти в цих точках - і . П’єзометричні напори в кожному перерізі - і . Лінію, що з’єднує відмітки п’єзометричних напорів, називають п’єзометричною.

Суму п’єзометричного і швидкісного напорів називають повним напором . Лінію, що з’єднує відмітки повних напорів, називають напірною.

Зміну величини п’єзометричного напору характеризує п’єзометричний похил

, (3.25)

де - нескінченно малий відрізок уздовж руху.

Внаслідок того, що тиск уздовж руху може зменшуватися або збільшуватися (якщо збільшується або зменшується швидкість), п’єзометричний похил може бути додатним або від’ємним.

Зміну величини повного напору характеризує гідравлічний похил

. (3.26)

Оскільки приріст завжди є від’ємним (напір зменшується вздовж руху), то гідравлічний похил завжди додатний.

Гідравлічний похил - це втрата повного напору, яку віднесено до одиниці довжини, тому

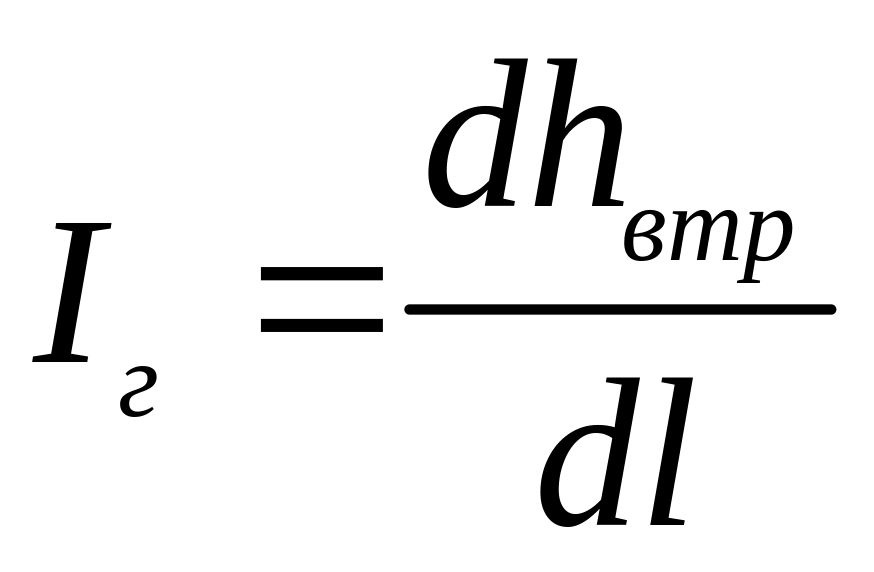. (3.27)

У загальному випадку втрати напору можуть виникати за рахунок зменшення всіх або деяких величин, що входять до рівняння Бернуллі.

На практиці водопровідні труби мають постійний переріз і швидкість в них постійна, а втрати напору відбуваються за рахунок зменшення п’єзометричного напору : у горизонтальних трубах втрати напору відбуваються за рахунок зменшення тиску , у безнапірних трубах – за рахунок зменшення відмітки .

3.9 Графічна ілюстрація зміни енергії вздовж трубопроводу

3.9.1 Зміна енергії вздовж трубопроводу для потоку ідеальної рідини

Розглянемо трубопровід, зображений на рисунку 3.20.

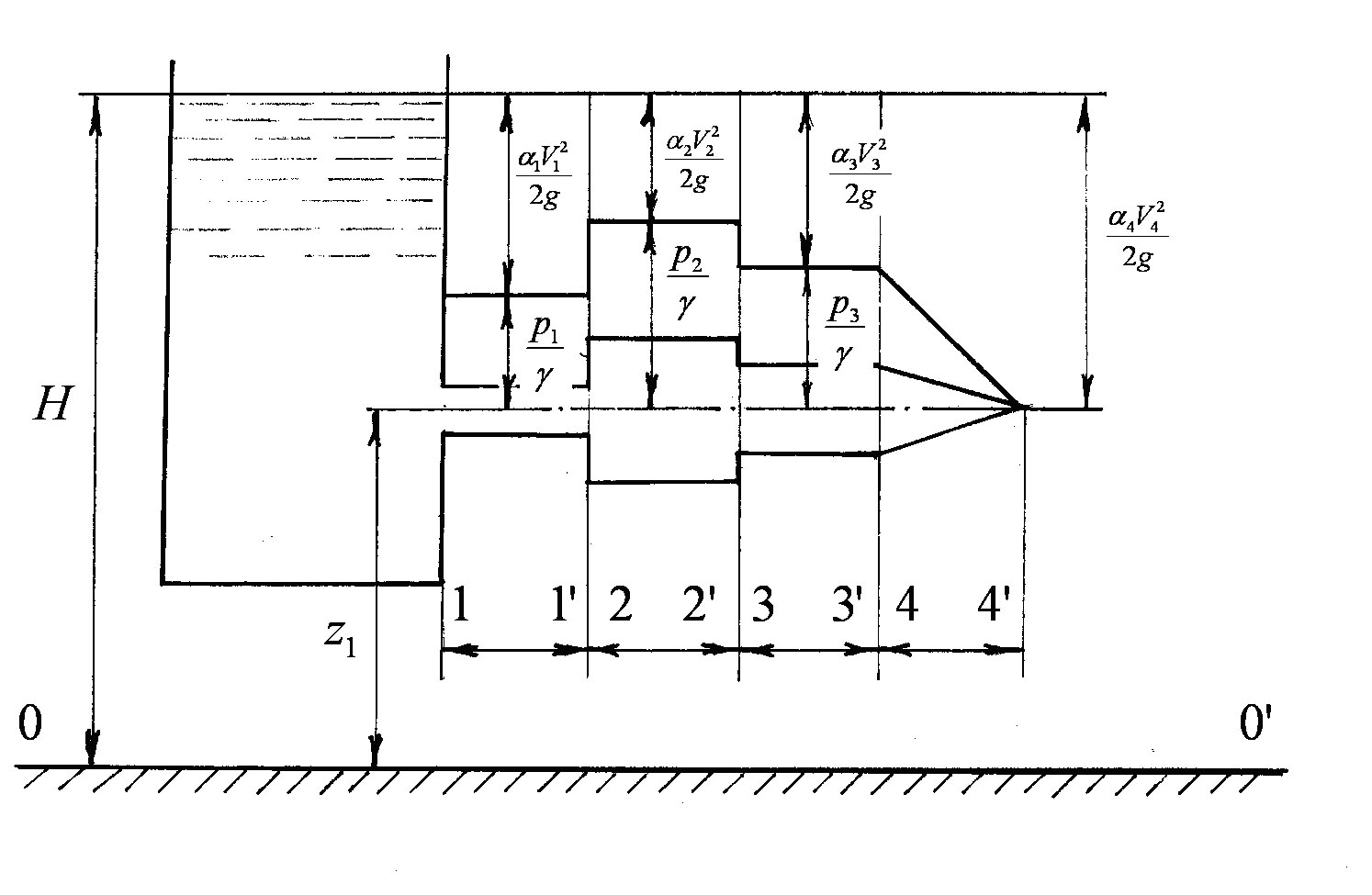
Рисунок 3.20

Якщо рідина ідеальна, втрат енергії вздовж трубопроводу немає, і для кожного перерізу виконується залежність

.

Відомо, що лінія повного напору для ідеальної рідини є горизонтальною. Аналізуючи характер зміни енергії вздовж трубопроводу, слід зробити наступні зауваження відносно лінії п’єзометричного напору:

а) якщо площа перерізу трубопроводу збільшується, швидкість і швидкісний напір зменшуються, п’єзометрична лінія йде вгору;

б) якщо площа перерізу трубопроводу зменшується, швидкість і швидкісний напір збільшуються, п’єзометрична лінія йде вниз;

в) якщо площа перерізу трубопроводу не змінюється, п’єзометрична лінія є горизонтальною прямою;

г) у випадку, коли вісь трубопроводу горизонтальна, її можна обрати за площину порівняння 0-0.