3.6.1.2 Геометричний зміст членів рівняння Бернуллі

Із гідростатики відомо, що вираз 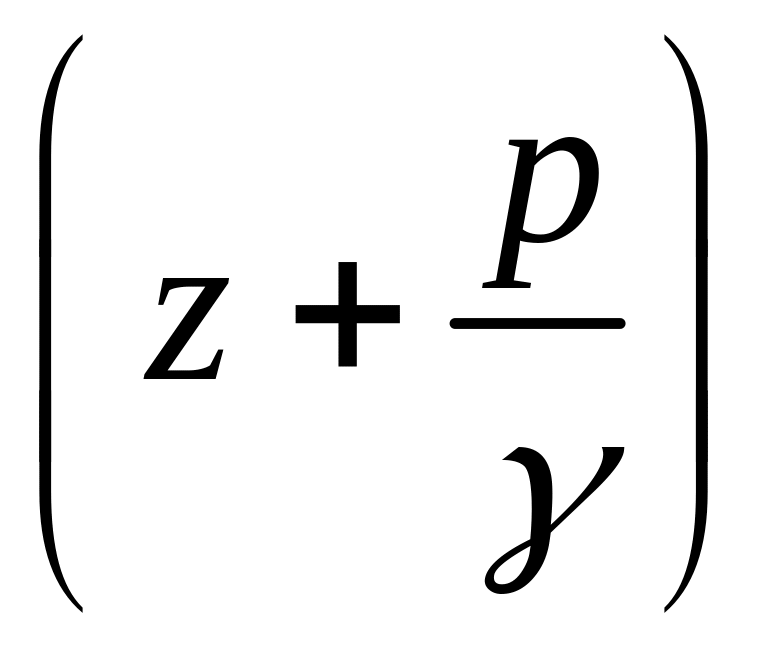є гідростатичний напір , який складається з лінійних величин – відмітки точки і п’єзометричної висоти .

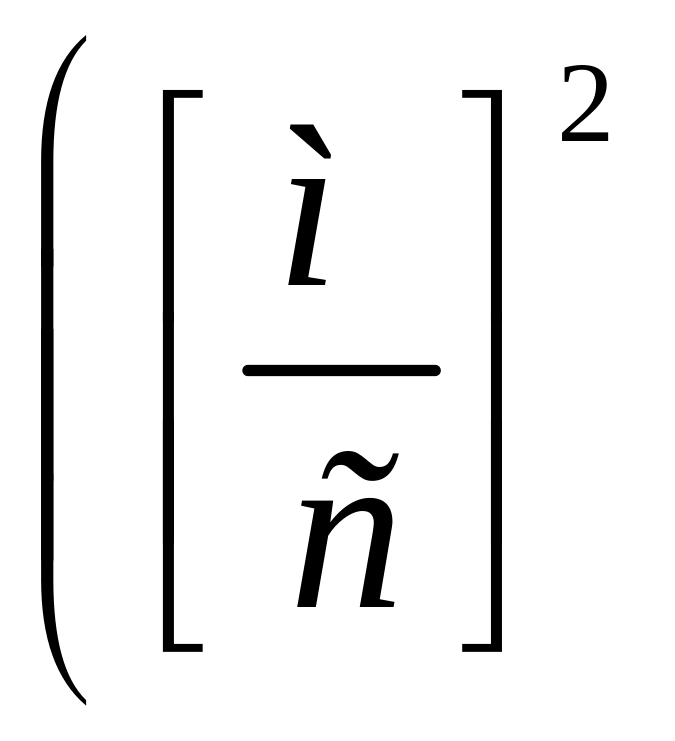
Величина також має лінійну розмірність  . Це - швидкісний напір.

Тоді рівняння Бернуллі можна записати так

, (3.17)

де - повний або гідродинамічний напір рідини.

Отже, рівняння Бернуллі є також рівнянням напору.

Рівняння Бернуллі є найважливішим рівнянням гідравліки. Воно встановлює залежність між положенням точки, тиском і швидкістю в будь-якому перерізі елементарної струминки й аналогічними характеристиками в іншому перерізі цієї самої струминки.

При сталих значеннях координат для всіх перерізів потоку ( ) із рівняння Бернуллі випливає дуже важлива властивість рідині, що рухається.

Складемо рівняння Бернуллі для перерізів потоку в точках 1, 2, 3 (рисунок 3.15).

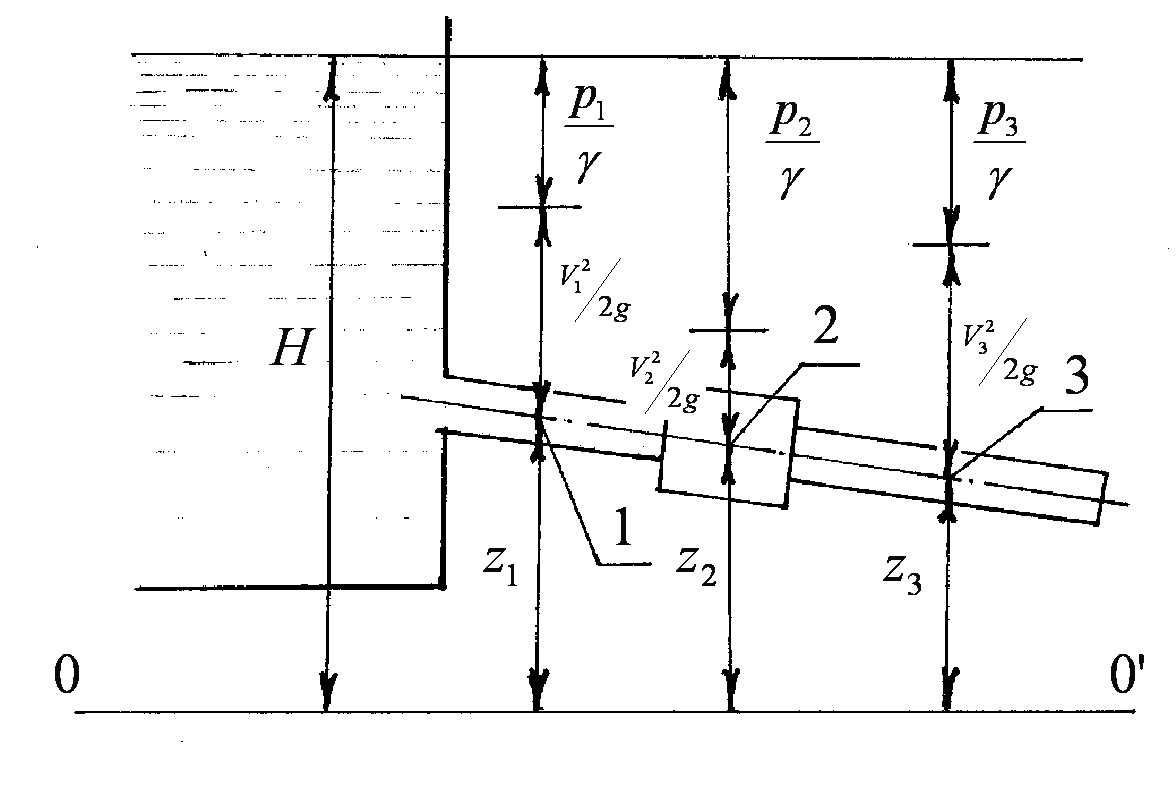
Рисунок 3.15

.

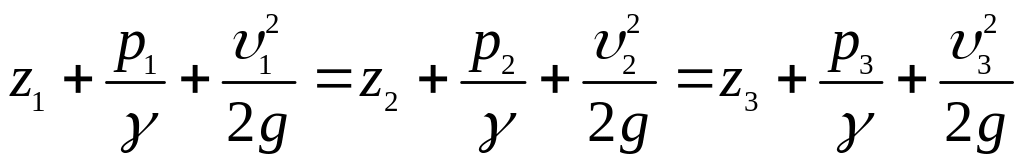Якщо , тоді

.

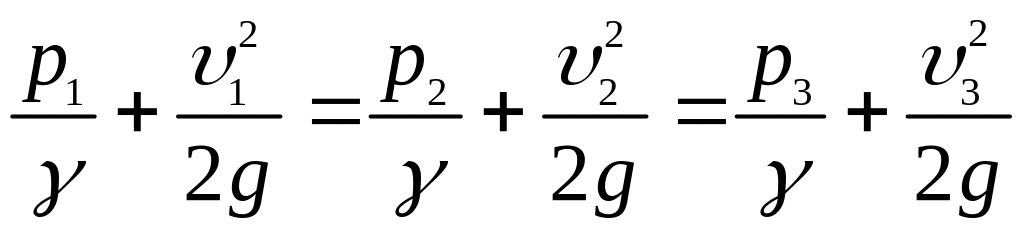Тобто для рідини, яка рухається, із зростанням швидкості тиск зменшується, а із зменшенням швидкості тиск збільшується.

Інакше – при зменшенні площі перерізу швидкість руху рідини збільшується, тиск зменшується; при збільшенні площі перерізу швидкість руху рідини зменшується, тиск збільшується.

Вищевказане є проявом механізму перетворення одного виду енергії в інший: потенціальної енергії в кінетичну і навпаки. У подальшому цю властивість рідини було використано у різноманітних технічних пристроях (рисунок 3.16).

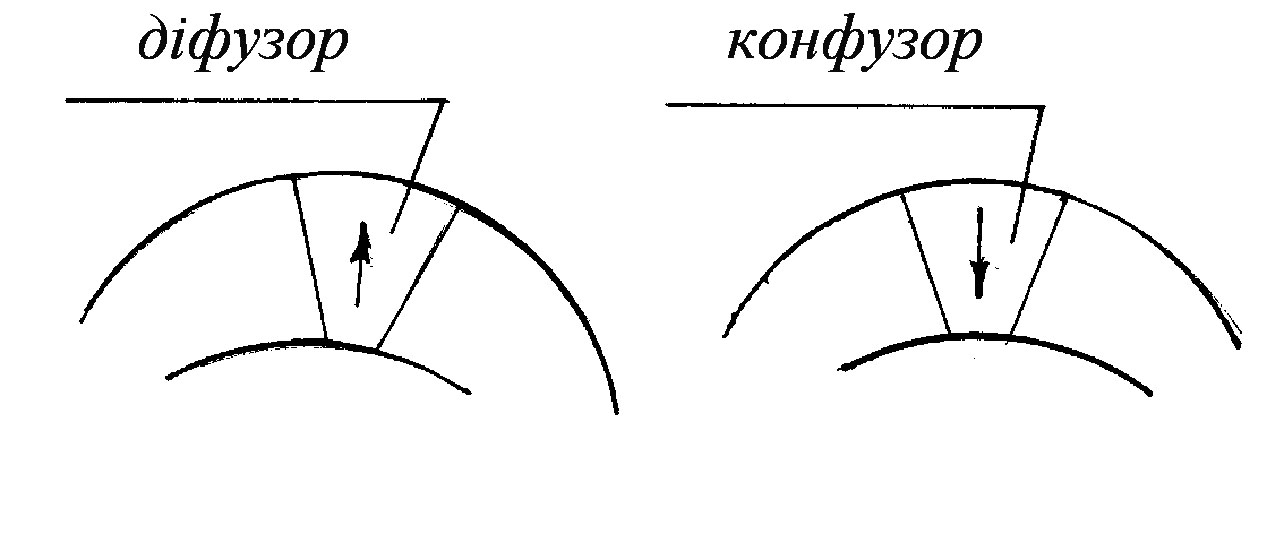
Рисунок 3.16

В загальному випадку рідина буде рухатися в напрямку від точки з більшим тиском до точки з меншим тиском. Тобто, якщо в точці А тиск р₁ = 20 Па, а в точці В тиск р₂ = 4 Па, то рідина буде рухатися від точки А до точки В (при і ).

3.6.2 Інші вирази для питомої енергії рідини

Повну питому механічну енергію однієї одиниці ваги рідини визначають за формулою

. (3.18)

Одиниця виміру - м.

Повну питому механічну енергію однієї одиниці маси рідини визначають за формулою

. (3.19)

Одиниця виміру - Н/м².

Повну питому механічну енергію однієї одиниці об’єму рідини визначають за формулою

. (3.20)

Одиниця виміру - м²/с².

У подальшому в розрахунках будемо користуватися виразом (3.18) без індексу „ ”:

.

3.7 Рівняння Бернуллі для потоку ідеальної рідини

Енергія потоку у живому перерізі складається із суми енергій елементарних струминок (рисунок 3.17).

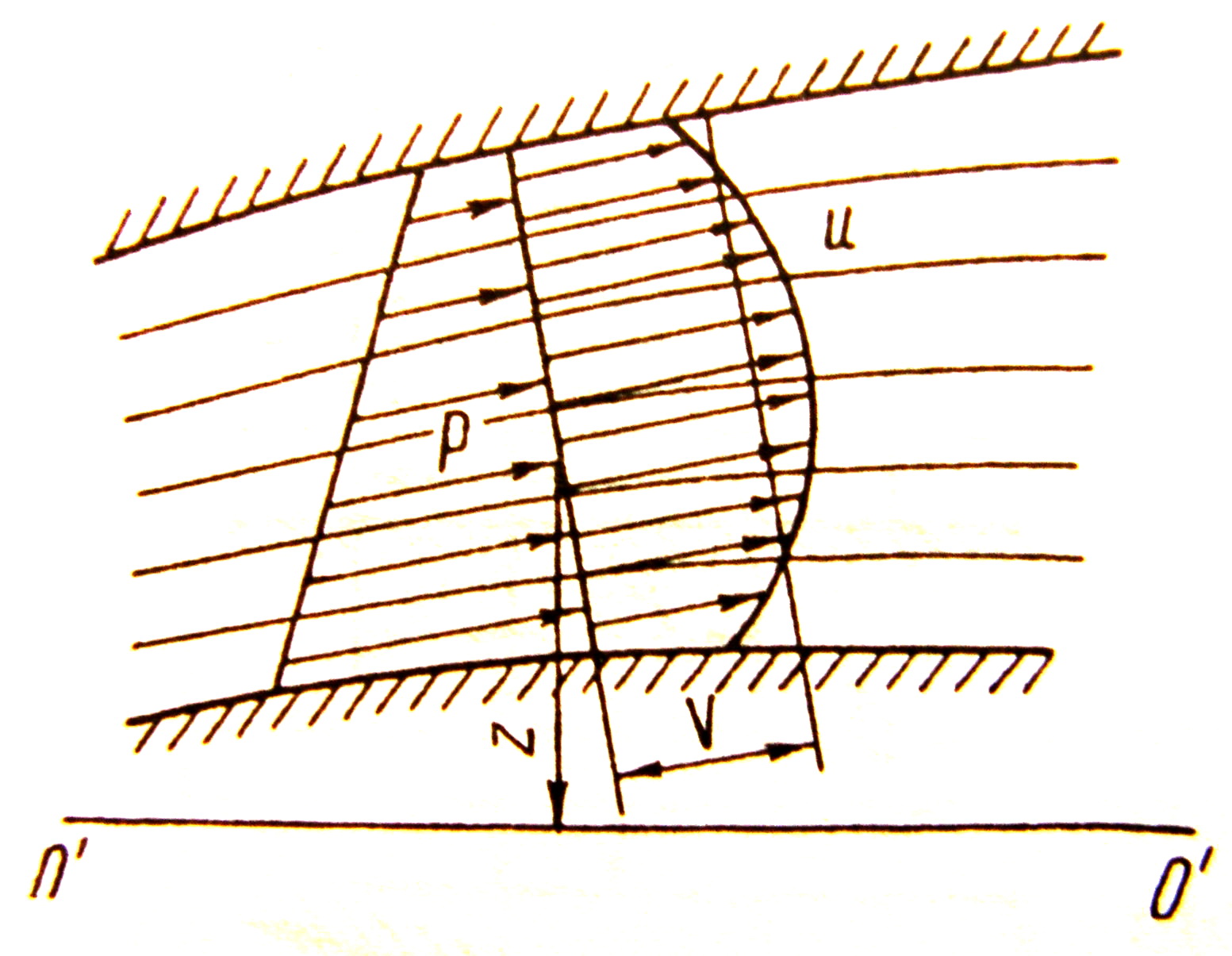
Рисунок 3.17

Якщо вираз (3.16) помножити на вагу рідини, яка протікає через живий переріз потоку, тоді, інтегруючи по площі живого перерізу, здобудемо повний (гідродинамічний) напір живого перерізу потоку

.

Якщо і віднести до центру ваги живого перерізу потоку, здобудемо питому енергію

.

Розглянемо два випадки: перший – всі частинки рідини проходять через живий переріз з однаковою швидкістю ( ); другий – швидкості частинок рідини в живому перерізі різні ( ) (рисунок 3.18).

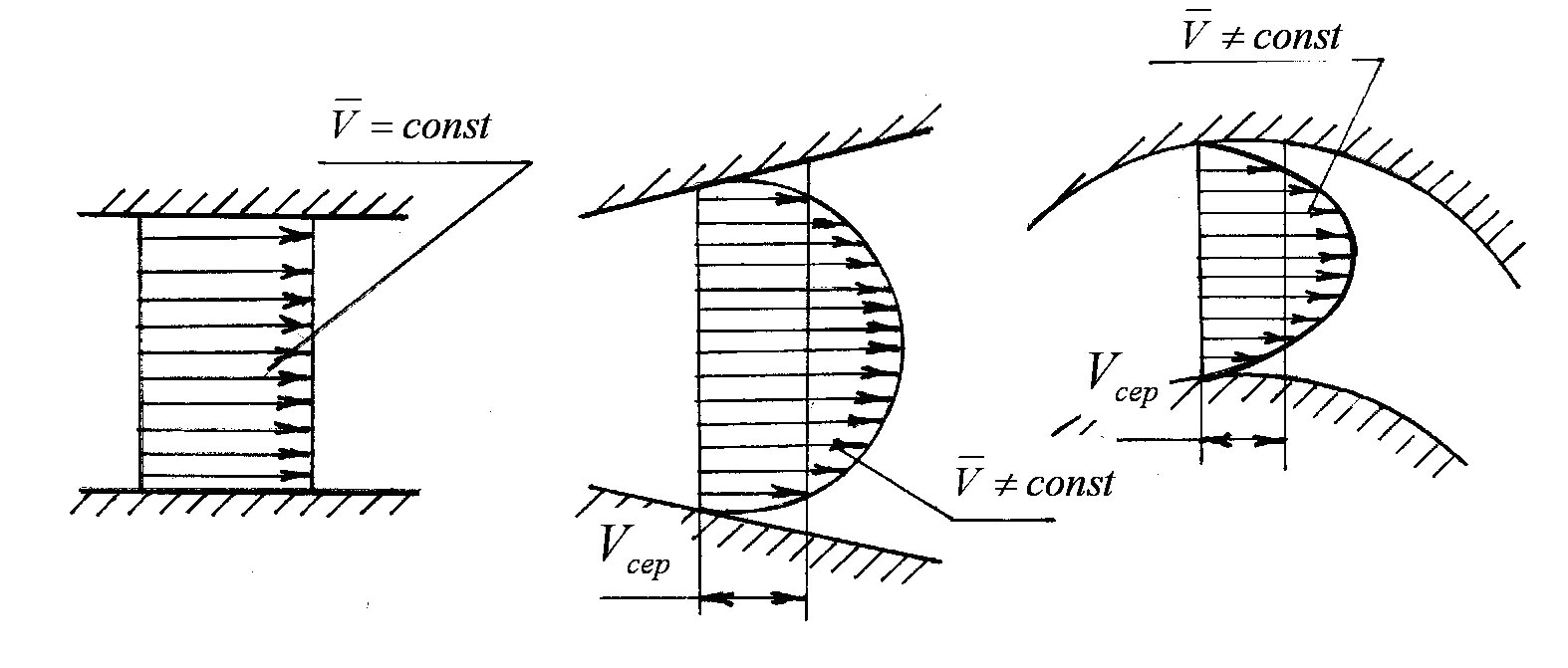
Рисунок 3.18

Перший випадок – ідеальний потік, другий – дійсний потік. Для наближення реальної епюри швидкості до ідеальної, треба ввести середню швидкість . Але кінетична енергія, яка підрахована по середній швидкості , буде відрізнятися від кінетичної енергії для дійсних величин швидкості. Для врахування нерівномірності розподілу швидкостей по перерізу введемо коефіцієнт відношення дійсної кінетичної енергії до кінетичної енергії, обчисленої за середньою швидкістю

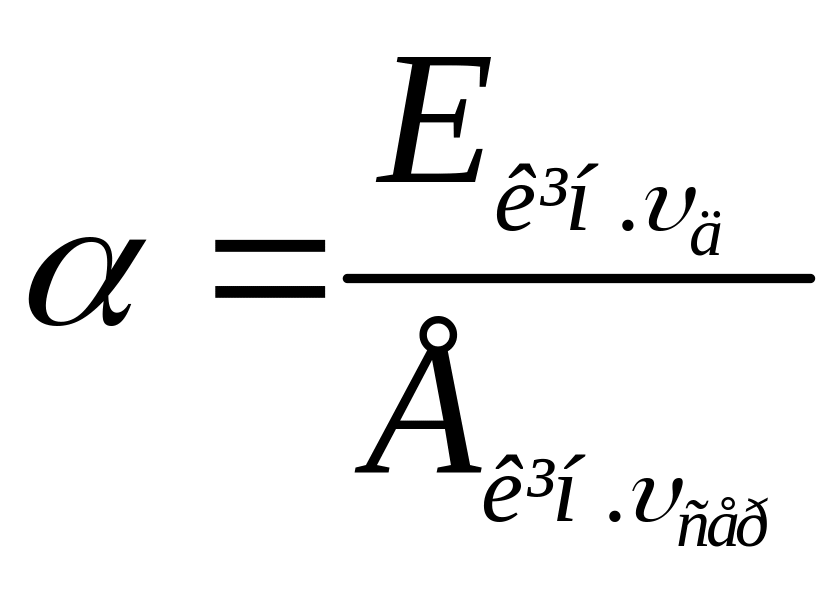. (3.21)

Коефіцієнт кінетичної енергії називають коефіцієнтом Коріоліса. З урахуванням (3.21) дійсна кінетична енергія в живому перерізі

.

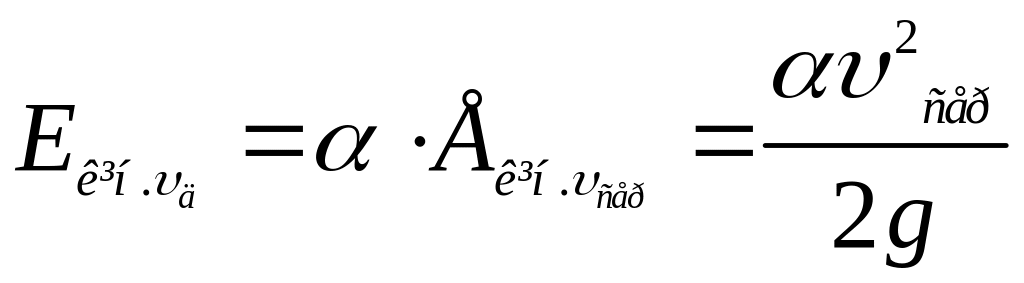Тоді рівняння Бернуллі для потоку ідеальної рідини матиме вигляд

, (3.22)

або

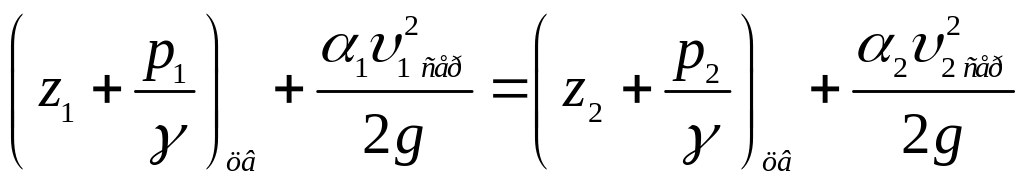. (3.23)

Фізичний зміст (енергетичний і геометричний) рівнянь (3.22), (3.23) той самий, що і для рівнянь (3.14), (3.15):

, - середня питома потенціальна енергія рідини в перерізах 1-1 і 2-2 відповідно;

, - дійсна питома кінетична енергія рідини в перерізах 1-1 і 2-2, яка підрахована по середній швидкості.

Значення коефіцієнта визначають за дослідними даними. У трубопроводах і каналах ; водночас у деяких випадках коефіцієнт може бути і значно менше за одиницю.