3.6 Рівняння Бернуллі для елементарної струминки ідеальної рідини

Другим основним рівнянням гідравліки після рівняння нерозривності є рівняння Бернуллі у різних його видах для різних випадків. Але фізичний зміст рівняння незмінний – закон збереження енергії: у замкнутій механічній системі енергія не зникає і не виникає, а лише переходить із одного виду в інший.

Розглянемо елементарну струминку ідеальної рідини з нескінченно малими розмірами перерізу і виділимо в неї об’єм рідини, що в момент часу розміститься між перерізами 1-1 і 2-2 (рисунок 3.13).

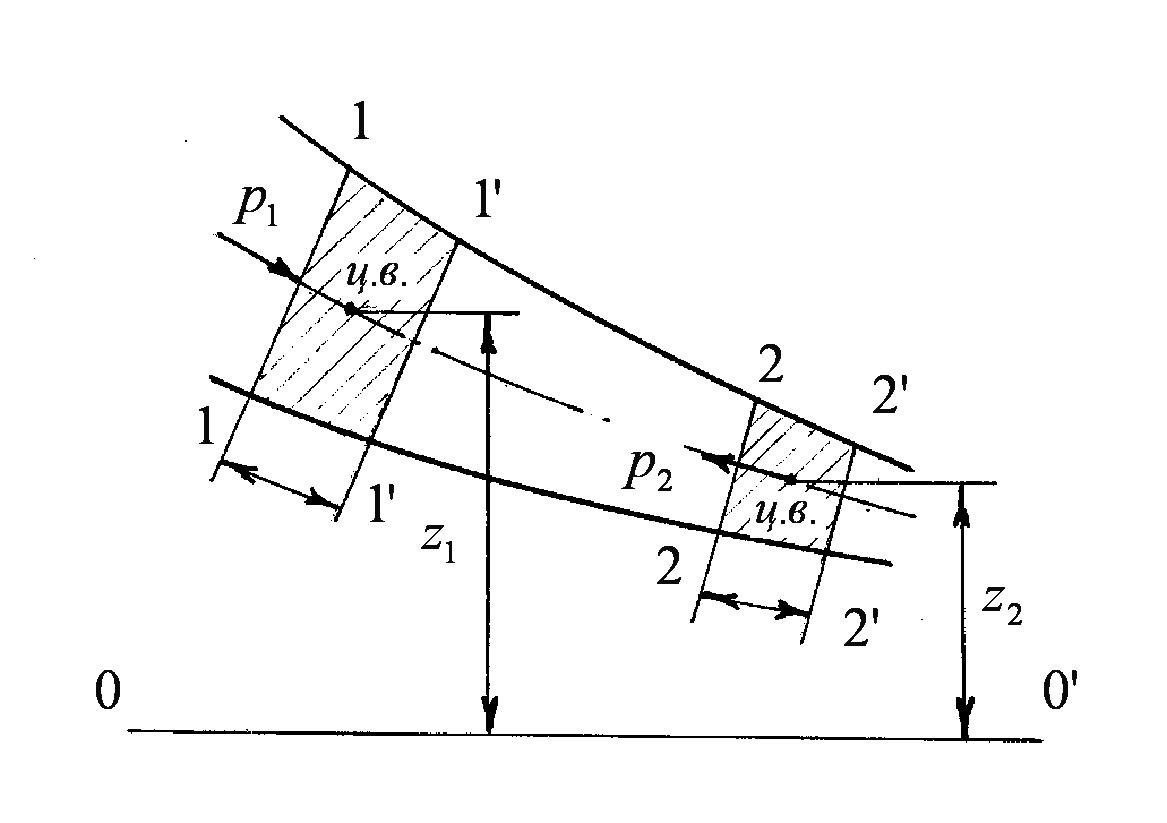
Рисунок 3.13

Через час цей об’єм займе положення між перерізами і . Примінимо до вибраного об’єму теорему про зміну кінетичної енергії. Згідно теоремі, зміна кінетичної енергії матеріального об’єму дорівнює роботі всіх зовнішніх сил, що діють на цей об’єм:

. (3.10)

В цьому випадку зміна кінетичної енергії здійснюється за рахунок роботи сили тиску і сили ваги  .

Позначимо площу перерізу 1-1 - , площу перерізу 2-2 - , переміщення перерізу 1-1 за час - , переміщення перерізу 2-2 за час - .

З урахуванням того, що , , знайдемо об’єми і (див. рис. 3.13):

,

.

Згідно закону нерозривності потоку , тому .

Маса об’ємів і буде

,

де - вага об’єму.

Тоді зміна кінетичної енергії

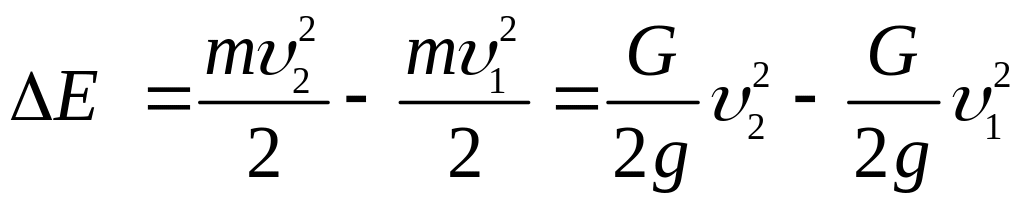. (3.11)

Визначимо тепер роботу сил, що діють на наш об’єм рідини:

а) роботу сили ваги по переміщенню об’єму визначимо як добуток сили ваги на шлях, що пройшов центр ваги об’єму по вертикалі:

, (3.12)

де і - висота розміщення центра ваги об’єму відносно площини порівняння 0-0;

б) роботу сили тиску по переміщенню об’єму визначимо як добуток сили тиску на площу перерізу і на величину переміщення:

. (3.13)

Підставляючи (3.11), (3.12), (3.13) в (3.10), дістаємо

.

Поділимо кожний член рівняння на і перегрупуємо, тоді

. (3.14)

Перерізи елементарної струминки нами були обрані цілком довільно, тому для любого перерізу струминки можна записати

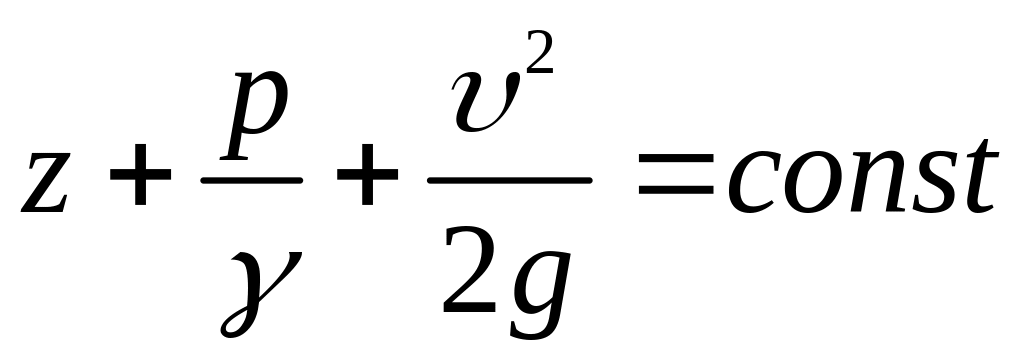. (3.15)

Вирази (3.14) і (3.15) називають рівнянням Д. Бернуллі для струминки ідеальної рідини.

3.6.1 Фізичний зміст членів рівняння Бернуллі

3.6.1.1 Енергетичний зміст членів рівняння Бернуллі

Для обчислення енергії нескінченно малої частинки масою з центром ваги у точці А, яка розміщена в межах елементарної струминки, необхідно визначити потенціальну і кінетичну енергію цієї частинки (рисунок 3.14).

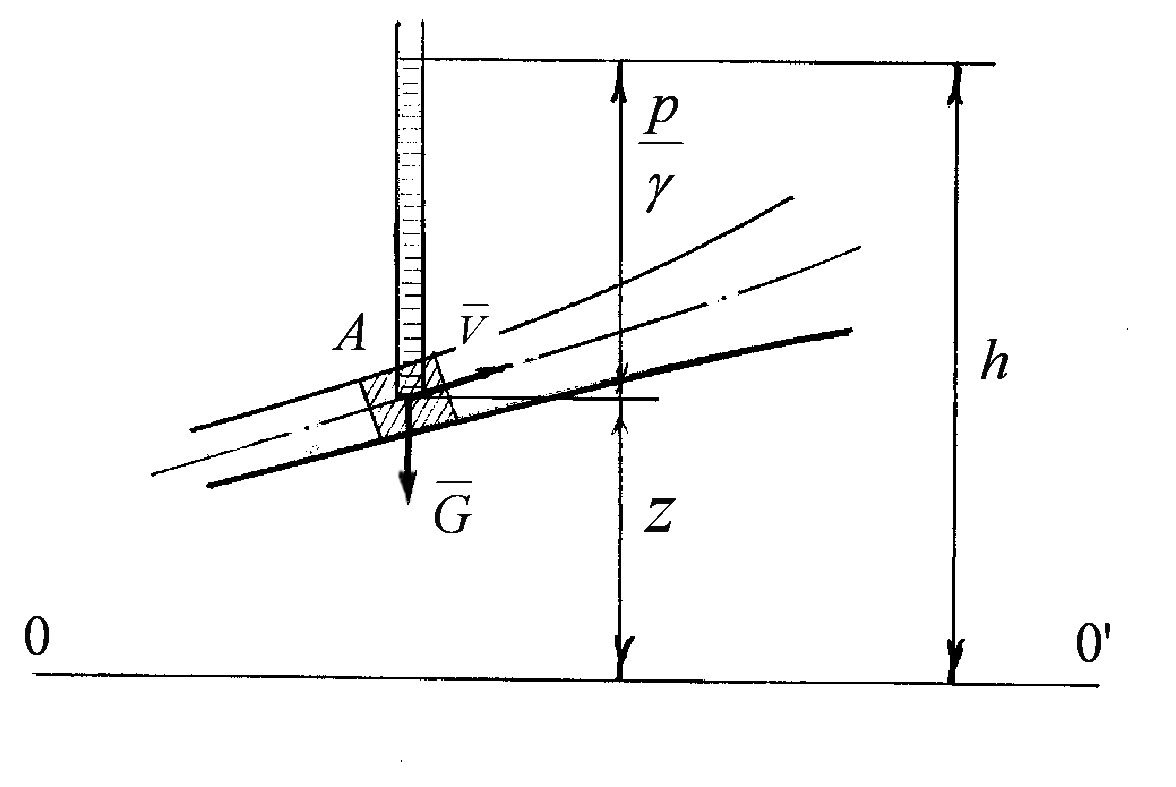
Рисунок 3.14

Загальна механічна енергія складається з суми потенціальної і кінетичної енергії.

Потенціальну енергію визначимо як добуток сили ваги, що діє на цю частинку, на висоту розміщення частинки над площиною порівняння 0-0:

.

Треба зазначити, що висота розміщення частинки складається з геометричної висоти і п’єзометричної висоти , бо рідина піднімається під дією тиску .

Тому

.

Для нескінченно малої частинки

.

Питома потенціальна енергія

.

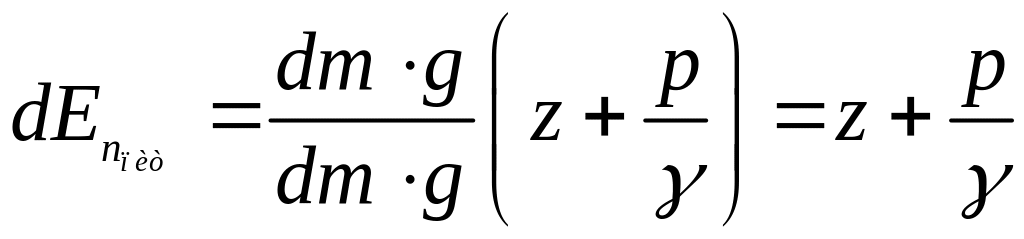Кінетична енергія

.

Для нескінченно малої частинки

.

Якщо розділити кінетичну енергію на одиницю ваги , то здобудемо питому кінетичну енергію

.

Повна питома енергія

,

або

, (3.16)

де - питома потенціальна енергія положення;

- питома потенціальна енергія тиску;

- питома кінетична енергія.

Вираз (3.16) для всіх перерізів струминки є величиною сталою.

Тобто для всіх перерізів елементарної струминки сума питомої потенціальної енергії і питомої кінетичної енергії є величиною сталою.

Енергетичний зміст рівняння Бернуллі – закон збереження енергії.

В подальшому повну питому енергію будемо називати напором рідини.

Одиниця виміру напору – м.