3.22.4 Траєкторія струменя
Розглянемо випадок, коли струмінь витікає з отвору чи насадку з горизонтальною швидкістю (рисунок 3.79).
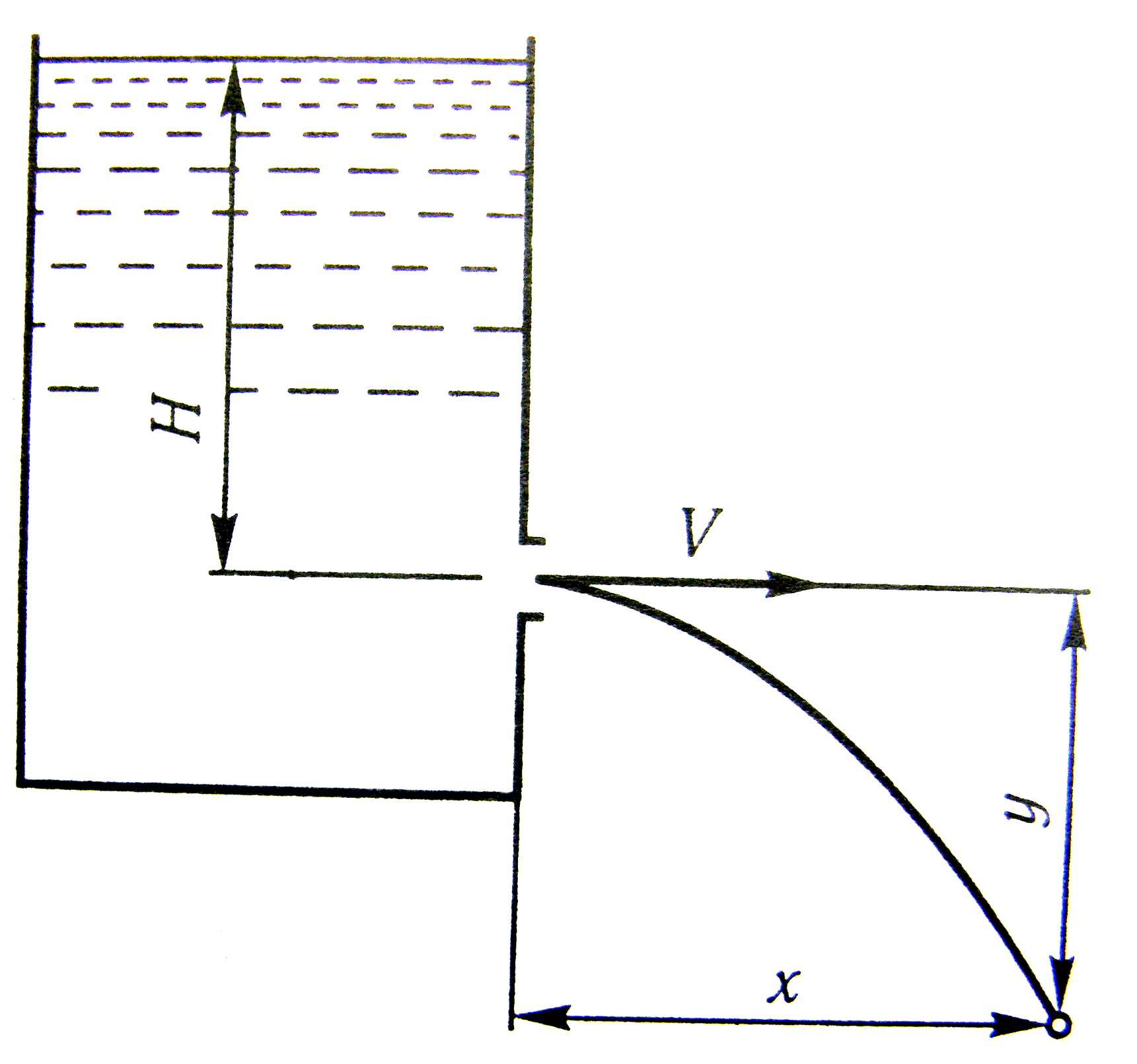
Рисунок 3.79
За час частина рідини в струмені подолає по горизонталі відстань :
.
За цей самий час частина рідини в умовах вільного падіння пройде вертикальний шлях :
.
Враховуючи
,
дістаємо
.
(3.109)
Вираз (3.109) є рівняння траєкторії струменя, що рухається в повітрі. Тобто траєкторія струменя є парабола.
Координати і у будь-якій точці струменя можна визначити за допомогою експерименту або задати їх і потім знайти швидкість:
.
Витрату можна визначити об’ємним способом і потім знайти коефіцієнти швидкості і витрати:
,
.
Коефіцієнт стиснення визначають
за формулою
.
Він є більш точним, ніж визначений
безпосереднім вимірюванням розмірів
перерізу струменя в повітрі.
3.22.5 Витікання рідини через отвори і насадки при змінному напорі (спорожнення резервуару)
Розглянемо спорожнення відкритого резервуару довільної форми через отвір чи насадку з коефіцієнтом витрати (рисунок 3.80).
Позначимо змінну висоту рівня рідини в резервуарі через , площу перерізу резервуара на висоті через , площу перерізу отвору (насадки) через .
Рисунок 3.80
Складемо рівняння витрати за нескінченно малий відрізок часу :
,
або
,
де
- зміна рівня рідини в резервуарі за час
.
Знак мінус в правої частині рівняння обумовлений тим, що при збільшенні величина зменшується.
Час, який потрібний для зміни рівня рідини в резервуарі на величину :
.
Вважаючи
,
після інтегрування маємо:
.
Час
можна визначити, якщо відомий закон
зміни площі
від висоти
.
Для призматичного резервуару цей закон
,
тому
,
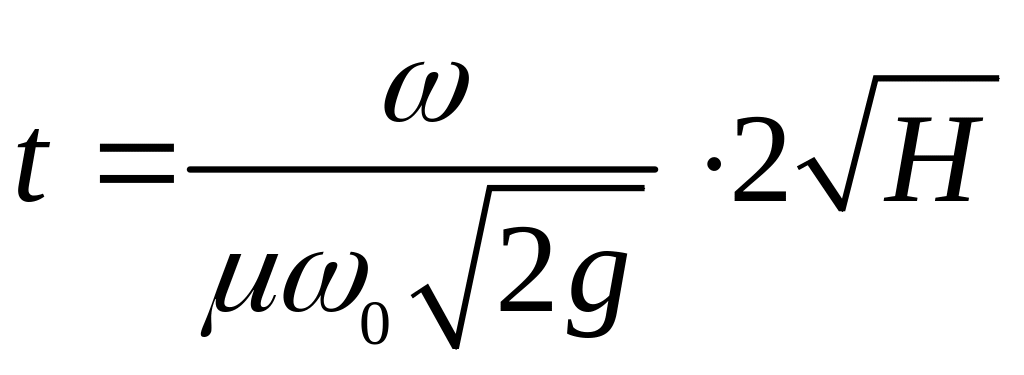або
.
(3.110)
В формулі (3.110) чисельник - це подвійний об’єм резервуару, знаменник - витрата через отвір чи насадку при початковому напорі .
Тобто час повного спорожнення резервуару удвічі більший від часу витікання такого самого об’єму рідини при сталому напорі, що дорівнює початковому.
Формула (3.110) показує час витікання основної маси рідини, тому що під час зниження рівня рідини в резервуарі умови її руху змінюються. При малих напорах утворюється воронка, разом з рідиною проривається повітря, витрата рідини зменшується і час витікання збільшується. Наприкінці спорожнення тільки окремі струминки і краплини стікатимуть вздовж кромок отвору.
3.22.6 Витікання рідини з дренованого резервуару
Дренований резервуар - це закритий резервуар, що з’єднаний з атмосферою через отвір чи трубопровід (рисунок 3.81).
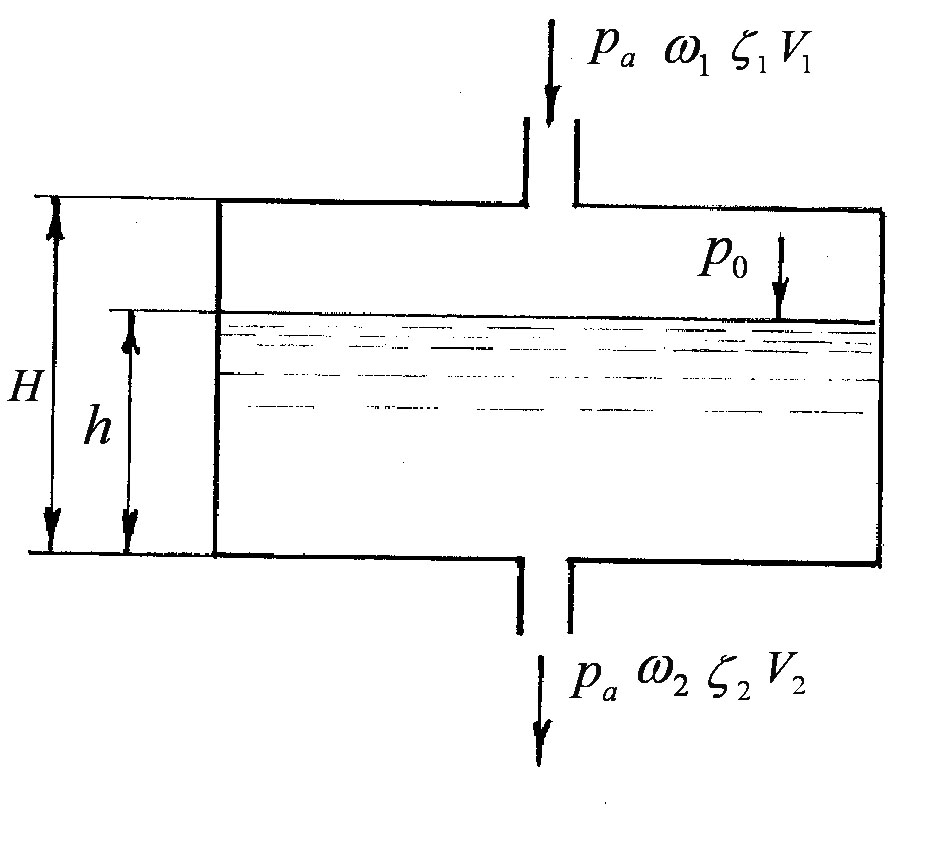
Рисунок 3.81
Потік повітря під атмосферним
тиском зі швидкістю
попадає в закритий резервуар через
отвір з площею
,
який має опір
.
В свою чергу рідина під тиском
зі швидкістю
витікає в атмосферу через донний отвір
площею
,
який має опір
.
Складемо рівняння Бернуллі для потоків повітря і рідини:
Використаємо рівняння витрати
.
Тоді, перетворюючи, дістаємо
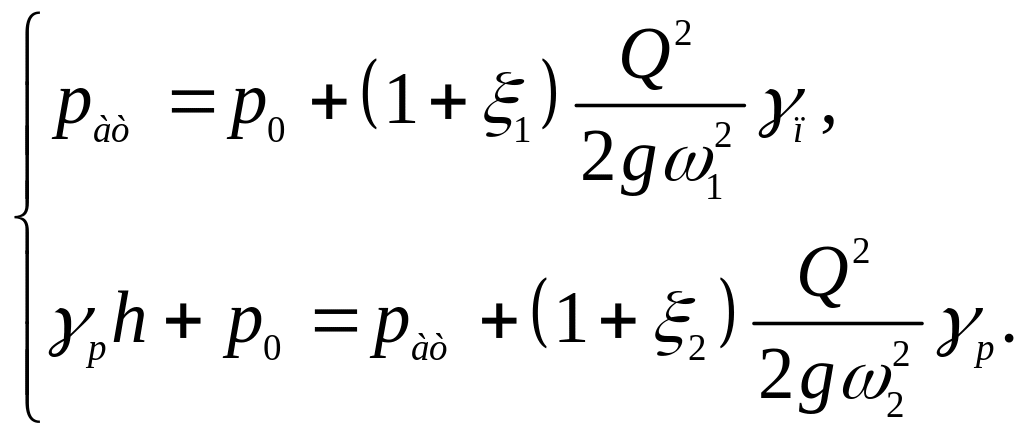
Для розв’язання системи рівнянь складемо ці рівняння і визначимо витрату . Тоді
Звідси
.
(3.111)
Баланс витрати рідини в даному випадку
.
Звідси
.
Для визначення часу витікання із дренованого резервуара підставимо вираз (3.110) для витрати і проінтегруємо по висоті резервуара. Тоді
.
Величини
відомі, тому другий добуток можна
замінити поправочним коефіцієнтом
:
.
Тоді час витікання із дренованого резервуару
.
(3.112)
Якщо доступ повітря в резервуар здійснюється через дренажний трубопровід, а витікання рідини – через спорожнюючий трубопровід, формула (3.112) теж справедлива. Але коефіцієнти і в даному випадку є сумарними для дренажного і спорожнюючого трубопроводів:
,
.
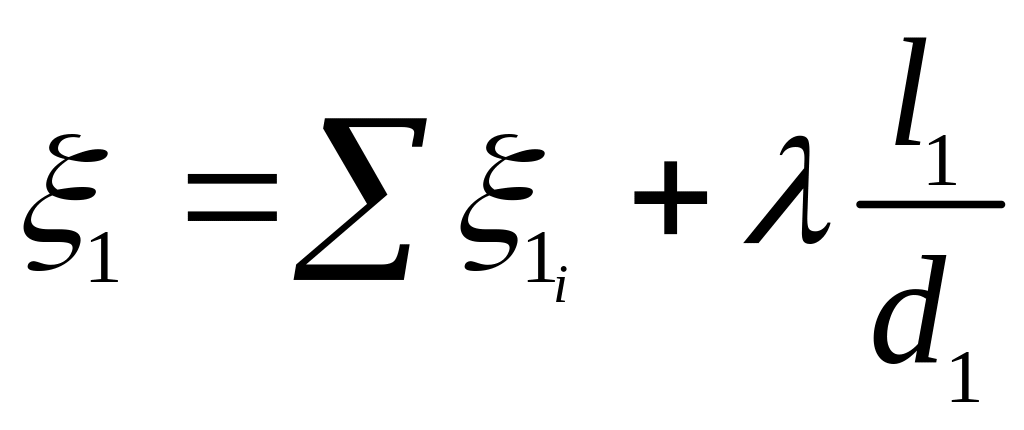