3.22 Витікання рідини через отвори і насадки

Вивчення витікання рідини через отвори і насадки обумовлено тим, що це явище досить часто має місце в техніці і в повсякденному житті, наприклад: спорожнення резервуарів; перетікання рідини з одного резервуару в інший, як у сполучену камеру; спеціальні пристрої – дроселі, де через малі отвори проштовхують рідину чи газ і створюючи опір гасять енергію; клапани і форсунки; струминна техніка, в тому числі струминні насоси.

Під час витікання рідини через отвори і насадки запас потенціальної енергії рідини в резервуарі перетворюється в кінетичну енергію струменя.

Струмінь не обмежений жорсткими стінками, називають вільним. В свою чергу вільні струмені можуть бути незатопленими і затопленими.

Незатоплені вільні струмені оточені газовим (повітряним) середовищем. Наприклад: пожежні і фонтанні струмені, струмені дощувальних апаратів.

Затопленим вільним струменем називають струмінь, що витікає в середовище з тією самою густиною, що й сам струмінь. Такі струмені бувають при випусках відпрацьованих промислових вод у басейни в системах водопостачання.

Метою розрахунків в даному випадку є визначення швидкості витікання, величини витрати і коефіцієнту опору для різних форм отворів і насадків, інколи – визначення конфігурації та дальності струменя.

3.22.1 Отвір у тонкій стінці

Якщо товщина стінки не впливає на умови витікання рідини, то такій отвір вважають отвором у тонкій стінці.

У цьому випадку рідина торкається тільки передній кромки отвору, що може бути при товщині стінки , яка менше від половини діаметра отвору - (рисунок 3.70 а), або при зрізі кромки отвору під гострим кутом (рисунок 3.70 б).

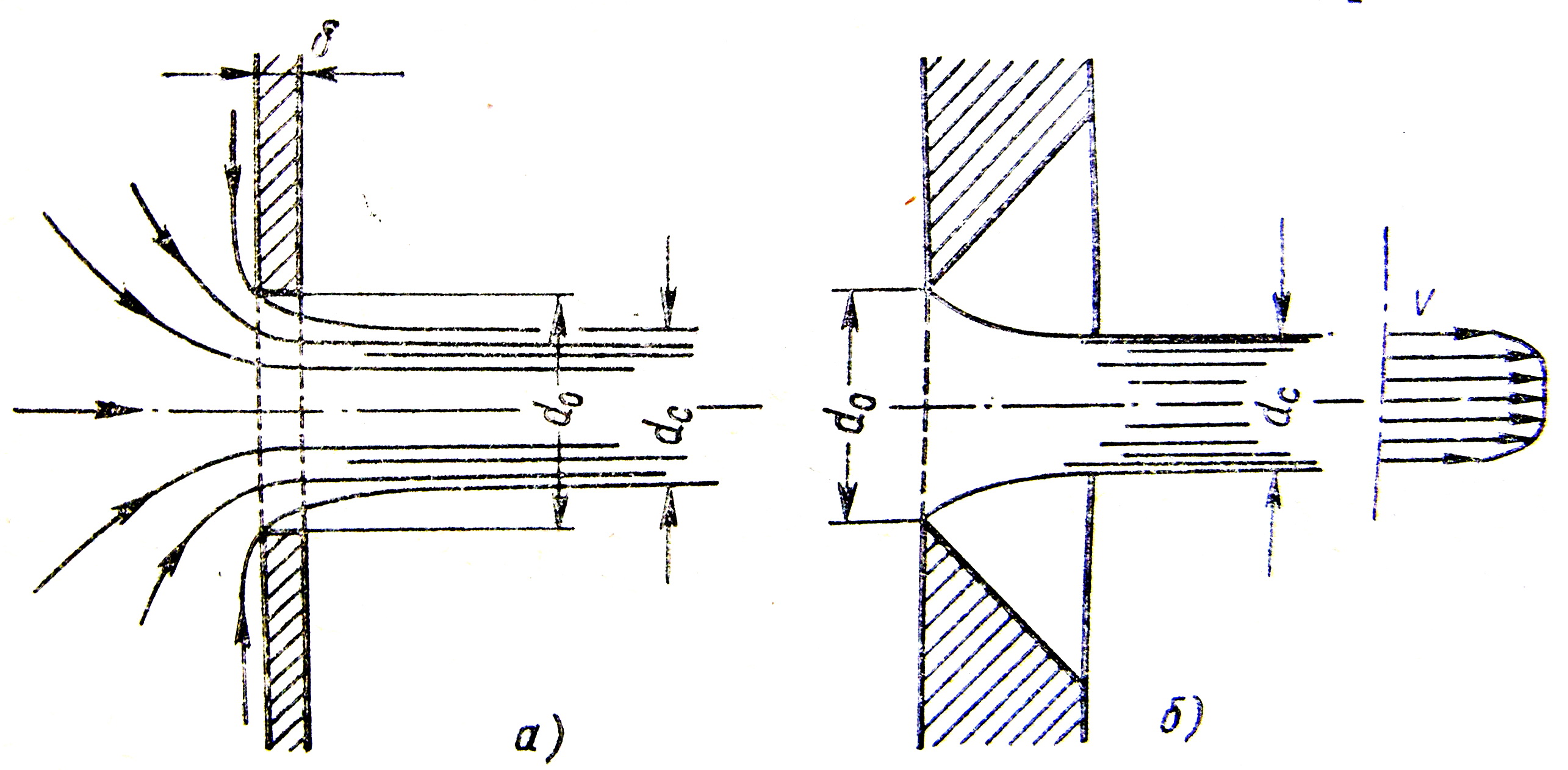
Рисунок 3.70

Умови витікання рідини в обох випадках однакові: частинки рідини наближаються до отвору зі всього об’єму по різним траєкторіям, струмінь відривається від стінці у кромки отвору і стискується. Стискання струменю обумовлено необхідністю переходу до осьового руху від різноманітних напрямків руху рідини в резервуарі.

Розрізняють досконале і недосконале стиснення (рисунок 3.71).

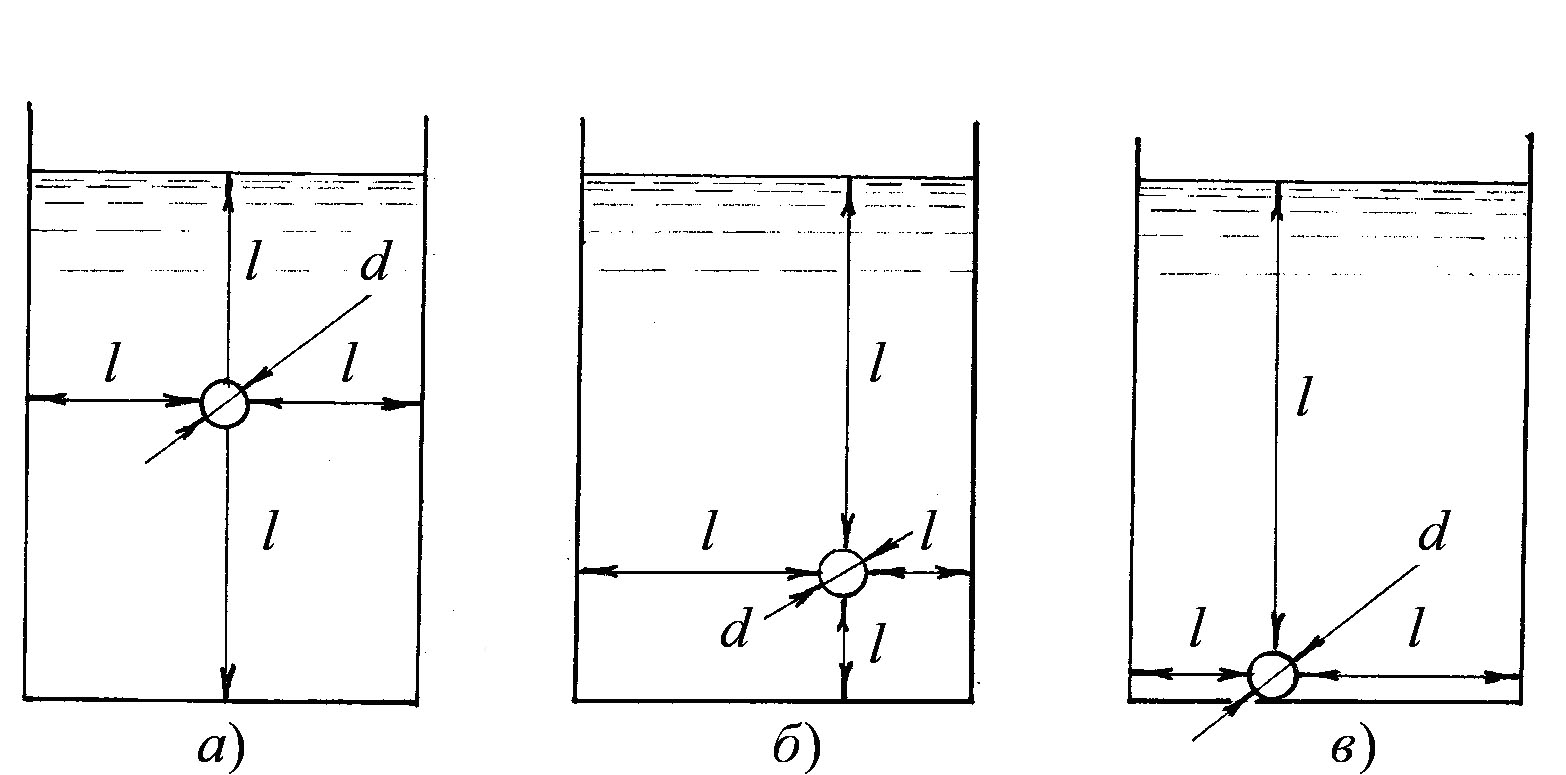
Рисунок 3.71

Якщо на формування струменя не впливають вільна поверхня, бокові стінки і дно резервуара, то стиснення вважають досконалим (див. рис. 3.71 а). Це можливо, коли отвір знаходиться на достатньої відстані від стінок і дна резервуара, тобто виконується умова

 ,

де - відстань до вільної поверхні, бокових стінок і дна резервуара;

- розмір отвору.

У випадку  стиснення вважають недосконалим (див. рис. 3.71 б). До того ж, якщо при підході до отвору потік з одного або кількох боків не має стиснення, то стиснення буде неповним недосконалим (див. рис. 3.71 в).

Величину стиснення характеризують коефіцієнтом стиснення струменя :

,

де - площа живого перерізу струменя;

- площа перерізу отвору.

Для круглого отвору

.

Коефіцієнт стиснення залежить від розташування отвору відносно вільної поверхні та числа Рейнольдса.

Визначимо швидкість витікання рідини через отвір (рисунок 3.72).

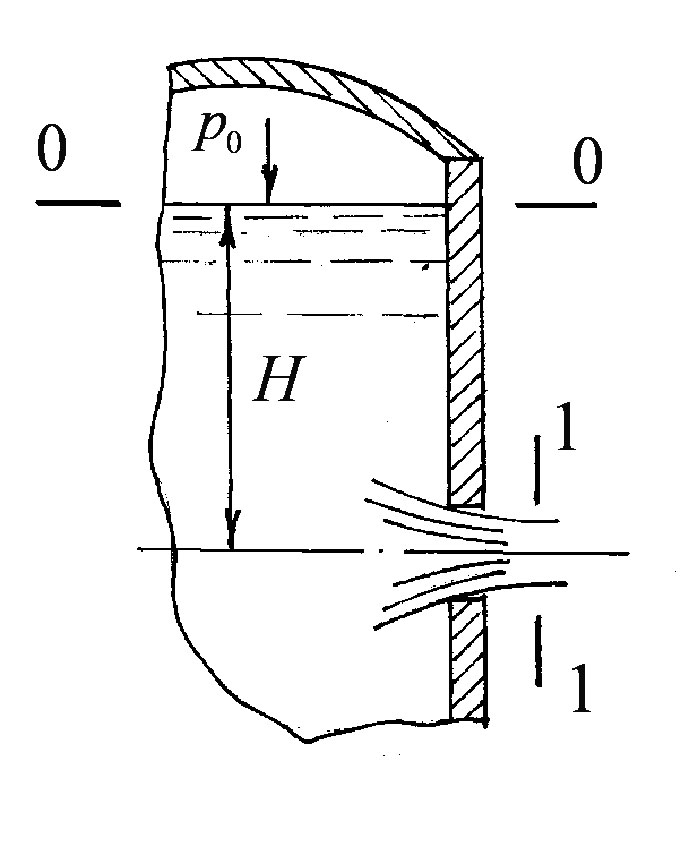
Рисунок 3.72

Складемо рівняння Бернуллі для перерізів 0-0 і 1-1:

,

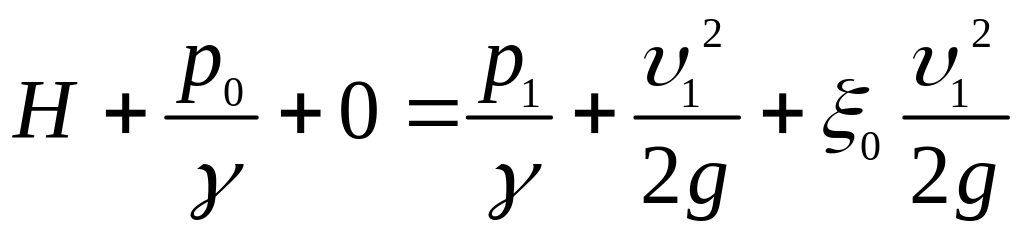де - коефіцієнт опору отвору;

- швидкість витікання в перерізі струменя 1-1.

Позначимо

,

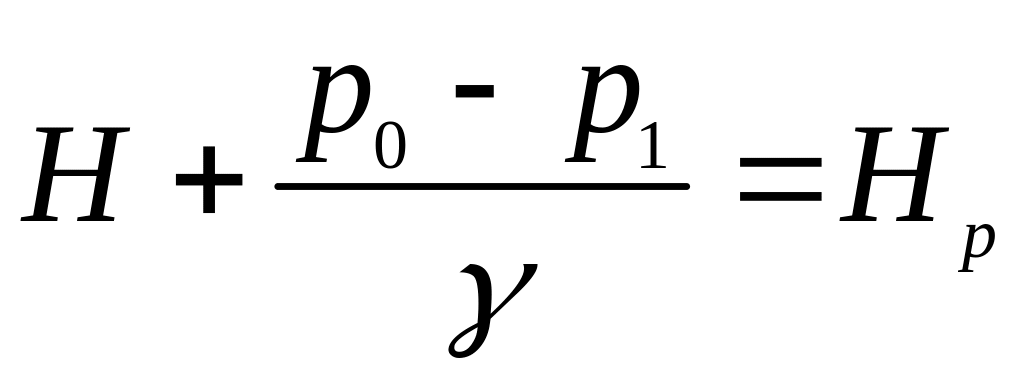де - розрахунковий напір.

Тоді

.

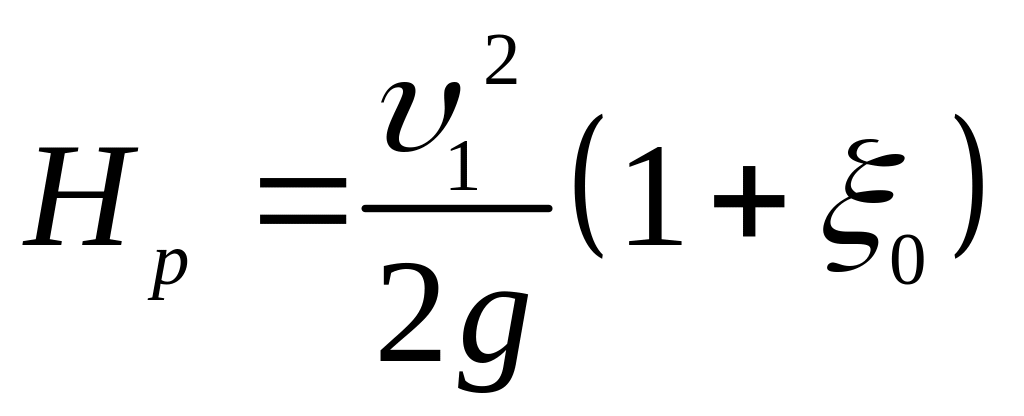Звідси

,

або

, (3.105)

де - коефіцієнт швидкості, який враховує втрати напору: .

Для ідеальної рідини , . Тобто для ідеальної рідини

.

Звідси випливає

.

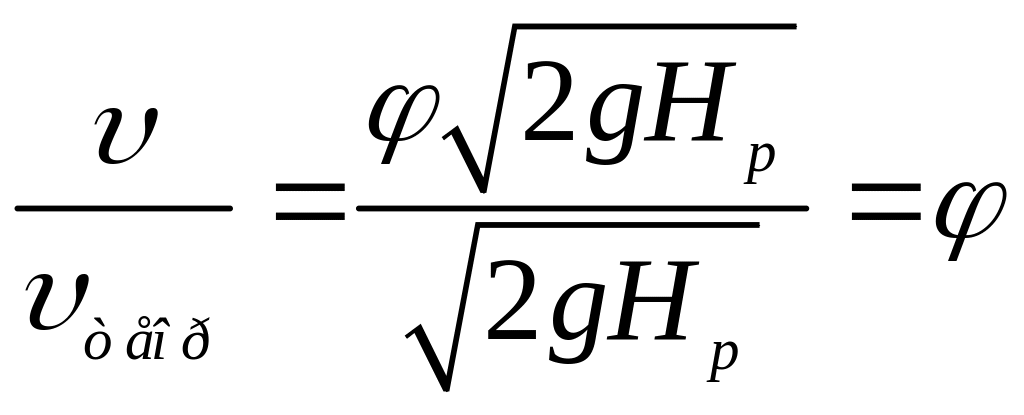Тобто коефіцієнт швидкості є відношенням дійсної швидкості до теоретичної, коли б рідина була ідеальною. Величина коефіцієнту менше за одиницю завжди: 1.

Якщо витікання рідини через отвір відбувається в атмосферу, тиск по всьому периметру струменя буде дорівнювати атмосферному.

Величину витрати визначимо як добуток площі перерізу струменя на швидкість витікання рідини через отвір:

.

Добуток коефіцієнтів і називають коефіцієнтом витрати :

.

Тому

. (3.106)

Очевидно

,

або

.

Тобто коефіцієнт витрати є відношенням дійсної витрати до витрати , якщо рідина була б ідеальною.

Витікання рідини через отвір визначають чотири коефіцієнта: коефіцієнт втрати напору , коефіцієнт стиснення струменя , коефіцієнт швидкості і коефіцієнт витрати . Всі вони залежать від числа Рейнольдса , який підраховують по теоретичної швидкості :

.

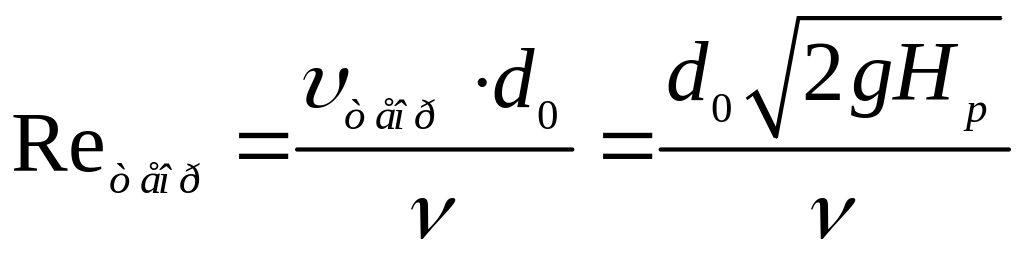Для кожного типу отвору коефіцієнти знаходять експериментально. При числах Рейнольдса від 10⁵ до  коефіцієнти мають значення: ; ; . Для орієнтовних розрахунків можна приймати наступні значення коефіцієнтів: ; ; ; .

Залежності коефіцієнтів , і від для круглого отвору наведені на рисунку 3.73.

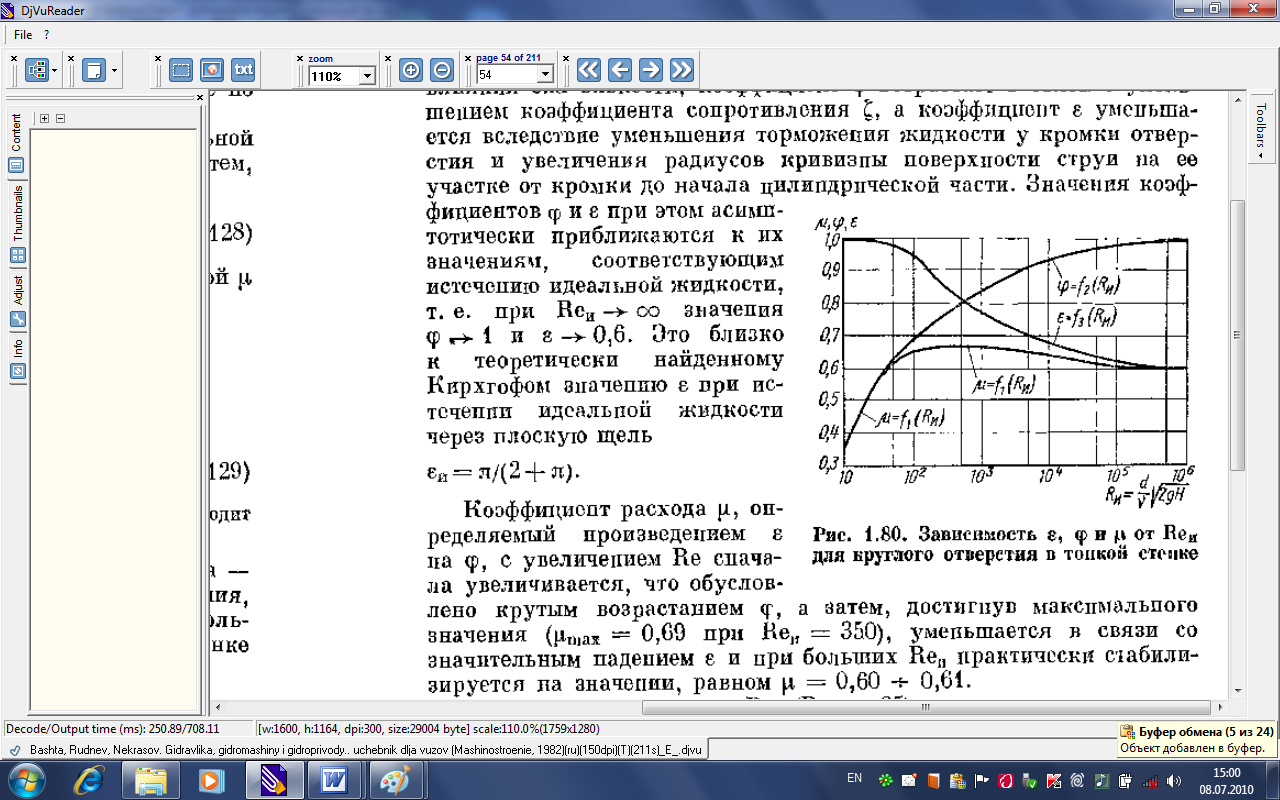
Рисунок 3.73

При недосконалому стисненні коефіцієнт відрізняється від коефіцієнта при досконалому стисненні:

,

де - відношення площі перерізу отвору до площі резервуару (рисунок 3.74).

Тобто

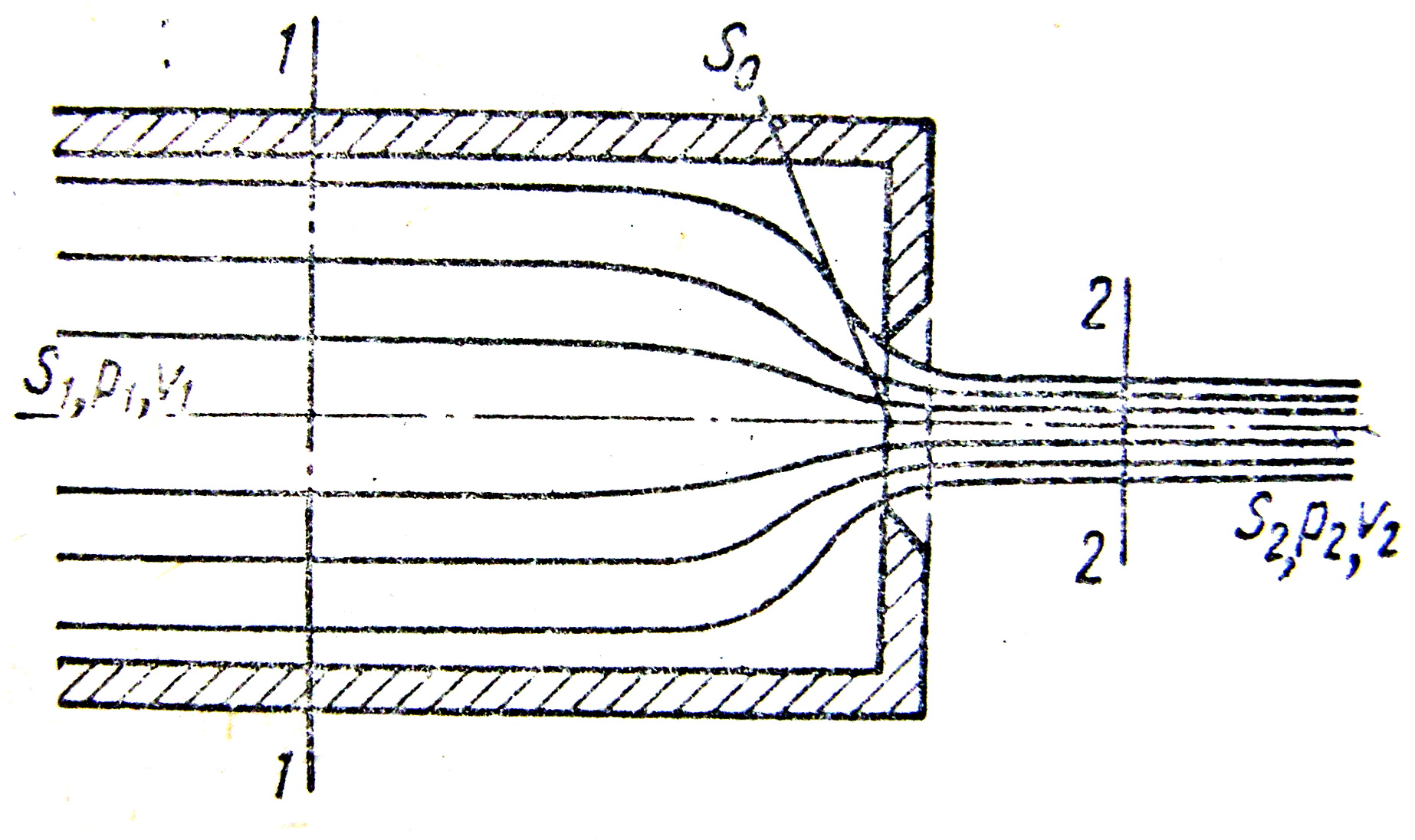
Рисунок 3.74

Можна вважати, що коефіцієнти і при недосконалому стиснені не залежать від співвідношення і . Тому коефіцієнт витрати при недосконалому стисненні

.

Тоді витрата при недосконалому стисненні

.

Для розрахунку в даному випадку слід врахувати швидкісний напір в резервуарі:

.

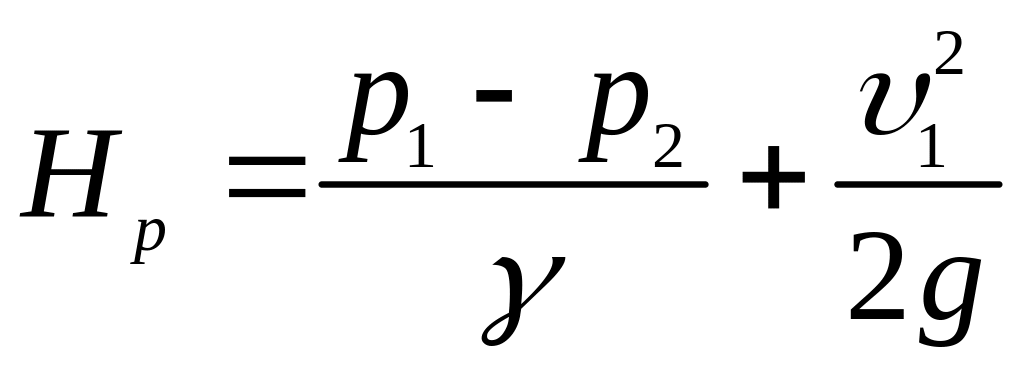Складемо рівняння Бернуллі для перерізів 1-1 і 2-2 (див. рис. 3.74):

.

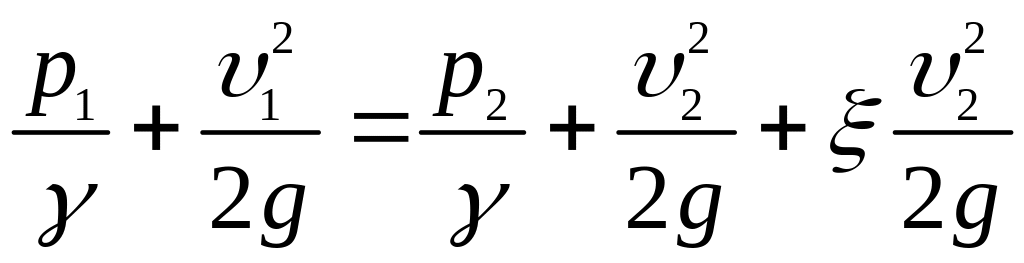З іншого боку

.

Звідси

,

або

.

Підставляючи вираз для в рівняння Бернуллі, дістаємо

.
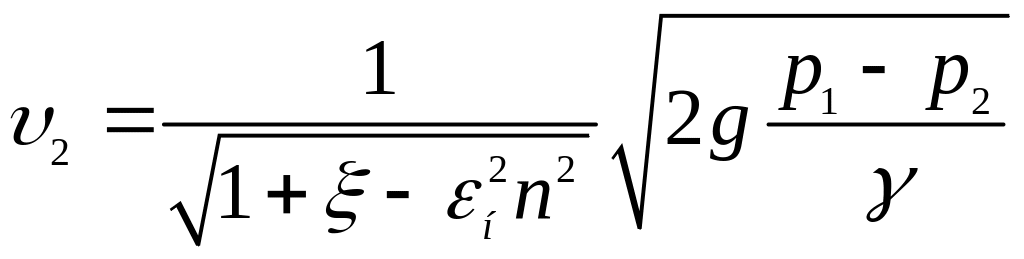