3.14 Ламінарна течія в круглій циліндричній трубі
При ламінарній течії частинки рідини рухаються шарами, паралельно один одному без перемішування, рух упорядкований. У круглій циліндричній трубі ламінарний режим руху встановлюється при числах Рейнольдса менше 2320 (Re 2320). Теорія ламінарної течії базується на законі тертя Ньютона
.
Розглянемо усталений ламінарний
рух рідини в прямій горизонтальній
круглій циліндричній трубі з внутрішнім
діаметром
.
Виділимо відрізок потоку довжиною
між перерізами 1-1
і 2-2
(рисунок 3.42).
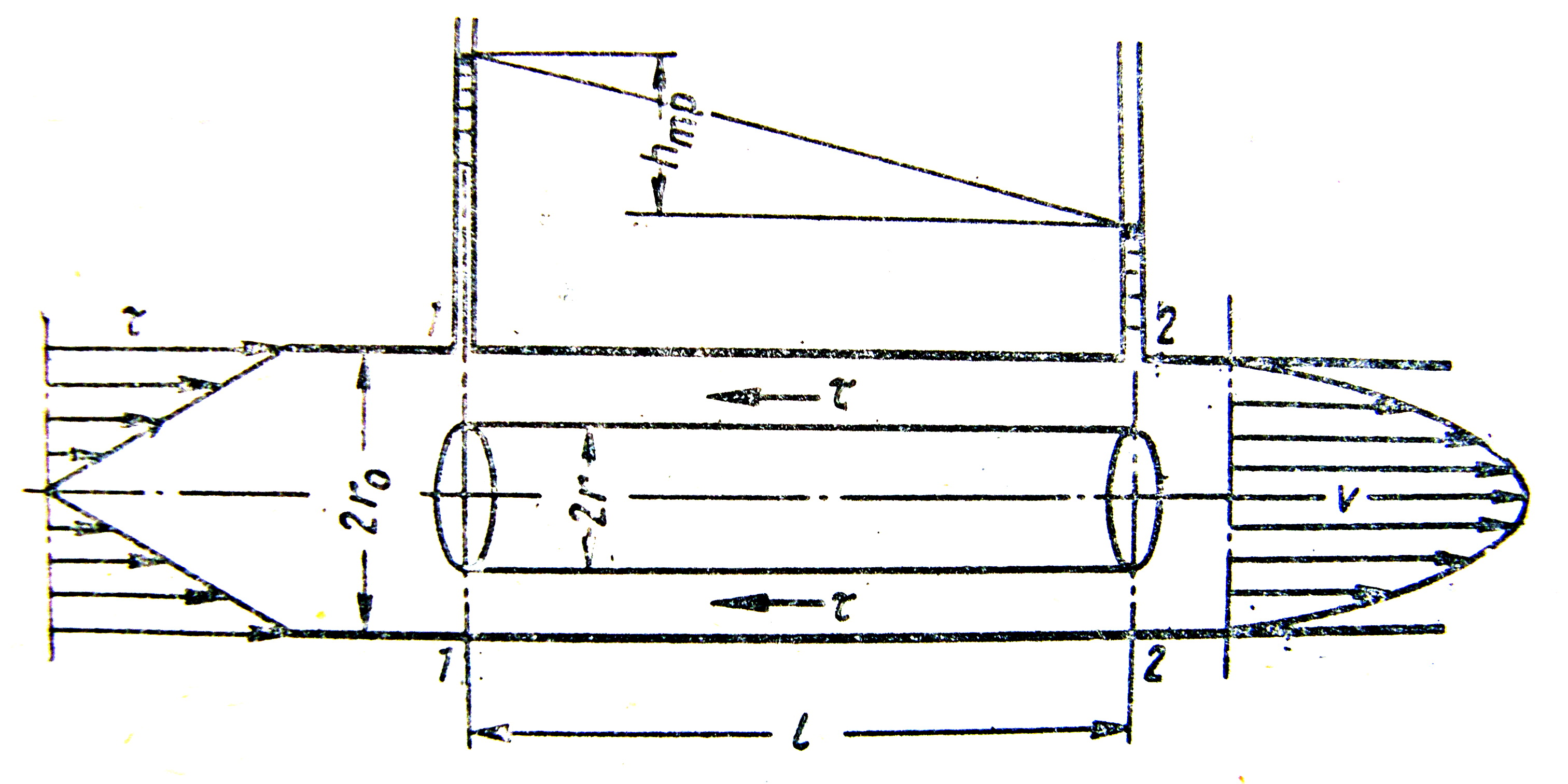
Рисунок 3.42
Складемо рівняння Бернуллі для перерізів 1-1 і 2-2
.
В цьому випадку
,
(труба горизонтальна, діаметр труби
однаковий для перерізів 1-1
і 2-2),
тому
.
Тобто втрати напору
на тертя визначаються за формулою
.
(3.67)
В потоці рідини вздовж осі труби виділимо циліндричний об’єм радіусом r, довжиною з основами в перерізах 1-1 і 2-2. Складемо рівняння рівноваги (сума сил тиску і тертя дорівнює нулю) для виділеного об’єму:
.
Звідси знайдемо
(3.68)
Тобто дотичне напруження в
перерізі труби змінюється за лінійною
функцією від радіуса
:
.
Із (3.68) випливає наступне:
якщо
,
тоді
;
якщо
,
тоді
.
Епюру дотичних напружень зображено на рисунку 3.42.
Для визначення закону розподілення швидкості в перерізі круглої труби при ламінарній течії підставимо значення з виразу (3.68) в закон тертя Ньютона. Тоді
,
або
.
Звідси
.
Після інтегрування маємо
,
або
(3.69)
Знайдемо постійну інтегрування
.
Якщо
,
тоді
.
Тому
.
Звідси
.
(3.70)
Підставляючи (3.70) в (3.69), дістаємо
.
(3.71)
Вираз (3.71) є закон розподілення швидкості в круглій циліндричній трубі при ламінарному русі рідини. Графічно цей закон зображується параболою другого ступеня.
Максимальна швидкість має місто в центрі перерізу при і визначається за формулою
.
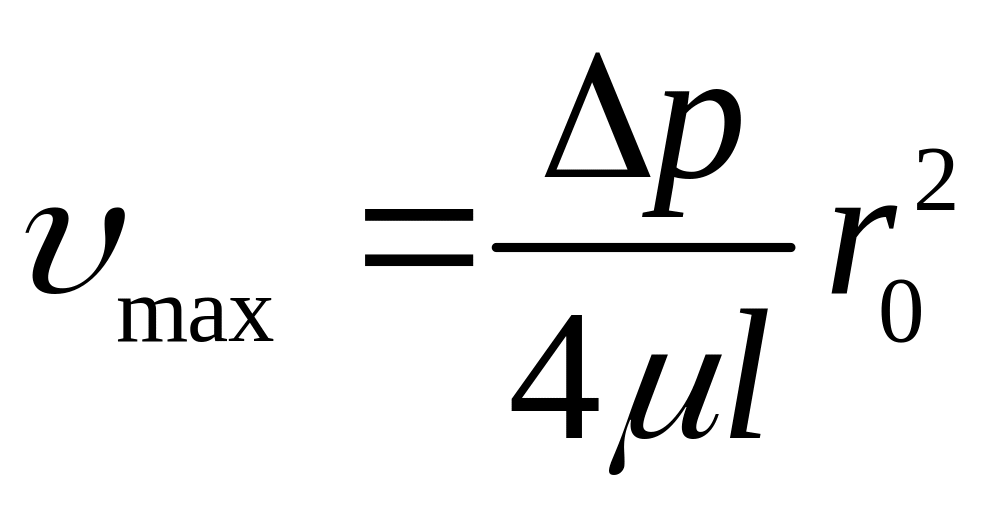(3.72)
Відношення
представляє собою гідравлічний
(п’єзометричний) похил, помножений на
.
Ця величина є постійною вздовж труби
однакового діаметра.
Використаємо знайдений закон
розподілення швидкості (3.71) для визначення
витрати
.
Елементарна витрата
через елементарну площу 
.
Розглянемо випадок, коли представляє кільце радіусом і товщиною (рисунок 3.43).
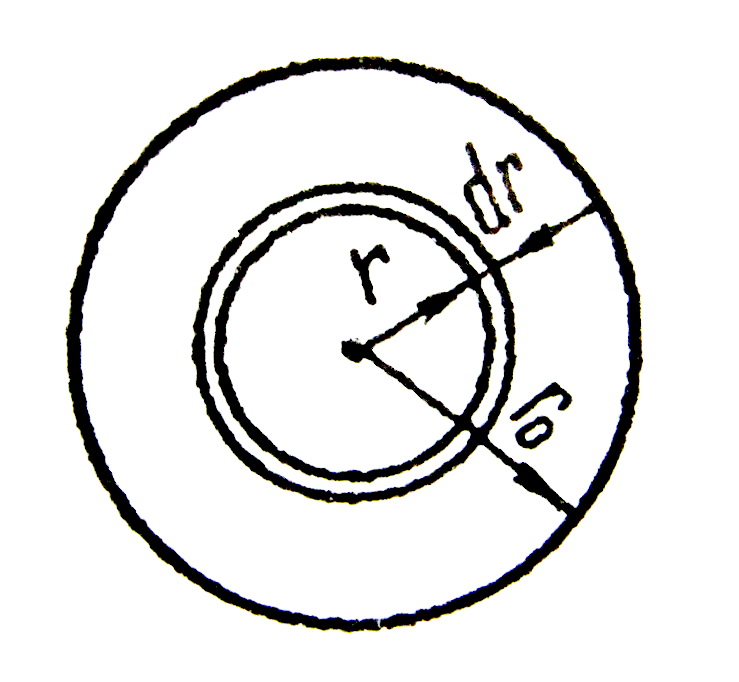
Рисунок 3.43
Тоді елементарну витрату можна визначити за формулою
.
Інтегруючи по площі перерізу від до , дістаємо
.
Остаточно
.
(3.73)
Середня швидкість в перерізі
.
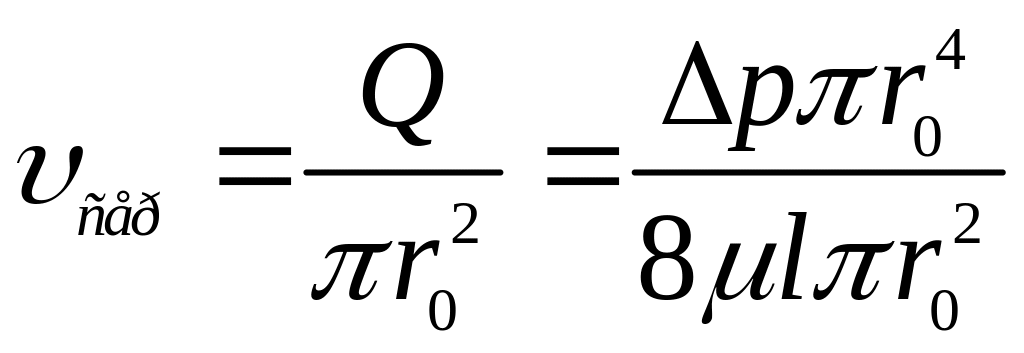Остаточно
.
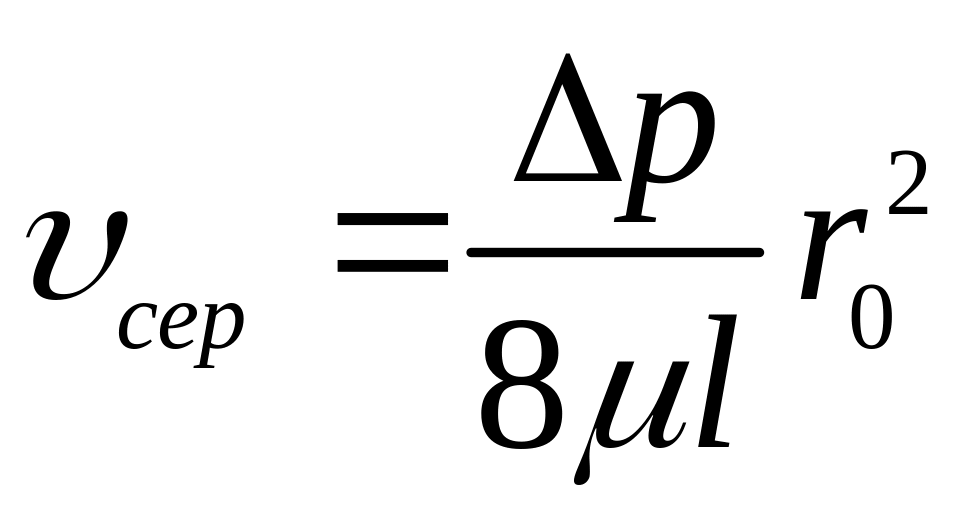(3.74)
Якщо порівняти вирази (3.72) і (3.74), можна зробити висновок:
.
(3.75)
Визначимо величину втрат
енергії по довжині
.
Раніше із рівняння Бернуллі було
встановлено
.
Із (3.73) знайдемо величину
:
.
Тоді
.
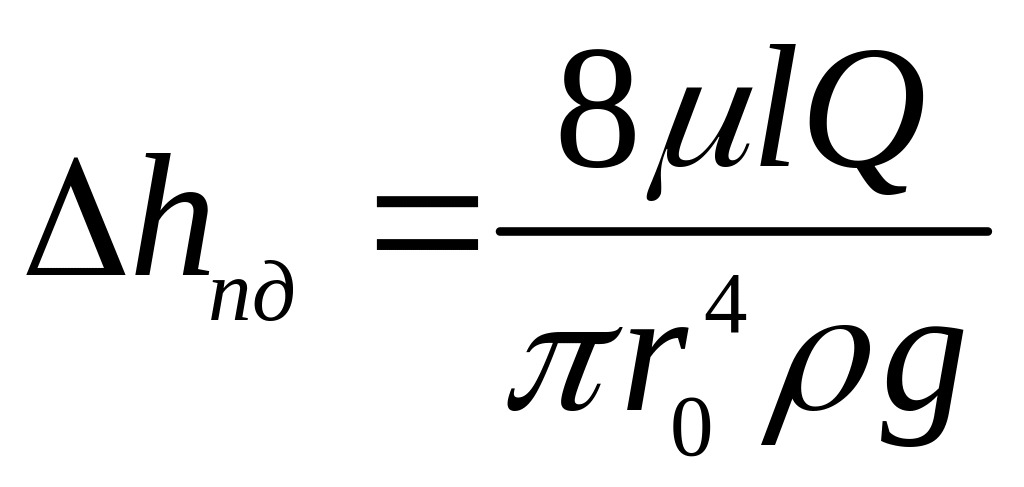(3.76)
Підставляючи в (3.76) кінематичну
в’язкість
і діаметр
,
дістаємо вираз
.
(3.77)
Аналізуючи (3.77), можна зробити
висновок: при ламінарній течії в
циліндричній трубі круглого перерізу
втрати енергії пропорційні довжині
труби
,
витраті
,
кінематичної в’язкості
і обернено пропорційні діаметру труби
піднесеному до четвертого ступеня.
Вираз (3.77) називають законом Пуазейля
і використовують для розрахунків
трубопроводу при ламінарній течії.
Раніше ми здобули вираз для визначення втрат по довжині
.
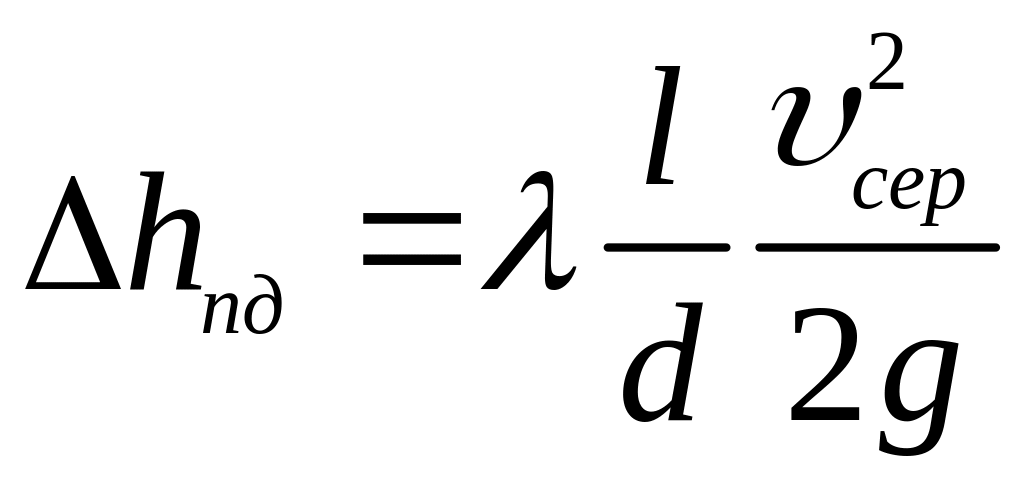Витрату для труби діаметром визначають за формулою
.
Підставляючи в вираз (3.77) значення , знайдемо коефіцієнт :
.
Тобто
.
(3.78)
Вираз (3.78) є формула Дарсі-Вейсбаха для визначення коефіцієнта опору по довжині при ламінарній течії.
Знаючи закон розподілення
швидкості по перерізу трубки (рівняння
(3.71)) і зв’язок між середньою швидкістю
і втратою напору
(рівняння (3.74)), знайдемо коефіцієнт
Коріоліса ,
який дозволяє враховувати нерівномірність
розподілу швидкості для ламінарної
течії в круглій циліндричній трубі
.
Враховуючи
,
і вирази (3.71), (3.74) для визначення
і
,
дістаємо
.
Введемо заміну
.
Тоді
.
Тобто кінетична енергія ламінарного потоку з параболічним розподілом швидкості у два рази більше кінетичної енергії того же потоку, але з рівномірним розподілом швидкості
.
(3.79)
Слід зауважити, що отримані результати добре відповідають експериментальним дослідженням. Тобто відповідають дійсності і не вимагають ніяких поправок за виключенням наступних випадків:
а) при дуже великих змінах тиску (ламінарна течія у зазорах і капілярах);
б) при наявності інтенсивного теплообміну із зовнішнім середовищем під час руху рідини по трубопроводу (якщо температура рідини, що рухається, значно відрізняється від температури зовнішнього середовища);
в) у коротких трубах.
При ламінарній течії рідини з резервуару в трубу розподіл швидкості на вході в трубу є рівномірним. Перерозподіл швидкості в параболу відбувається під дією сил в’язкості і обумовлений необхідністю проходу через незмінну площу даної витрати (рисунок 3.44).
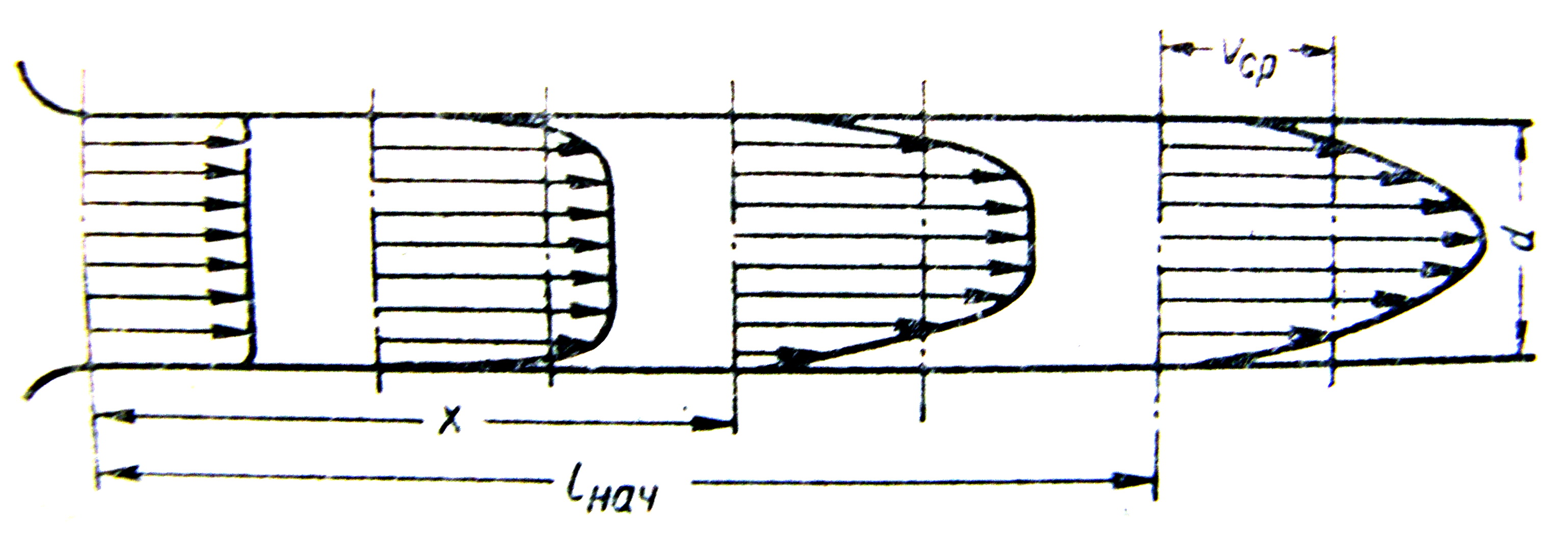
Рисунок 3.44
Ділянку труби, де встановлюється параболічний розподіл швидкості, називають початковою ділянкою ламінарної течії. Для визначення довжини початкової ділянки користуються формулою Шіллера
.
(3.80)
При
отримуємо максимально можливу довжину
початкової ділянки
.
(3.81)
Втрату напору для ділянки
труби довжиною
визначають за формулами (3.77) і (3.78), але
з уточнюючим коефіцієнтом
,
який враховує збільшення опору на
початковій ділянці труби. Для коротких
труб величина коефіцієнту
значно відрізняється від одиниці.
Коефіцієнт опору для початкової ділянки труби визначають за формулою
.
(3.82)