3.13.3.5 Поступове звуження каналу

Відрізок каналу, який поступово звужується, називають конфузором (рисунок 3.37).

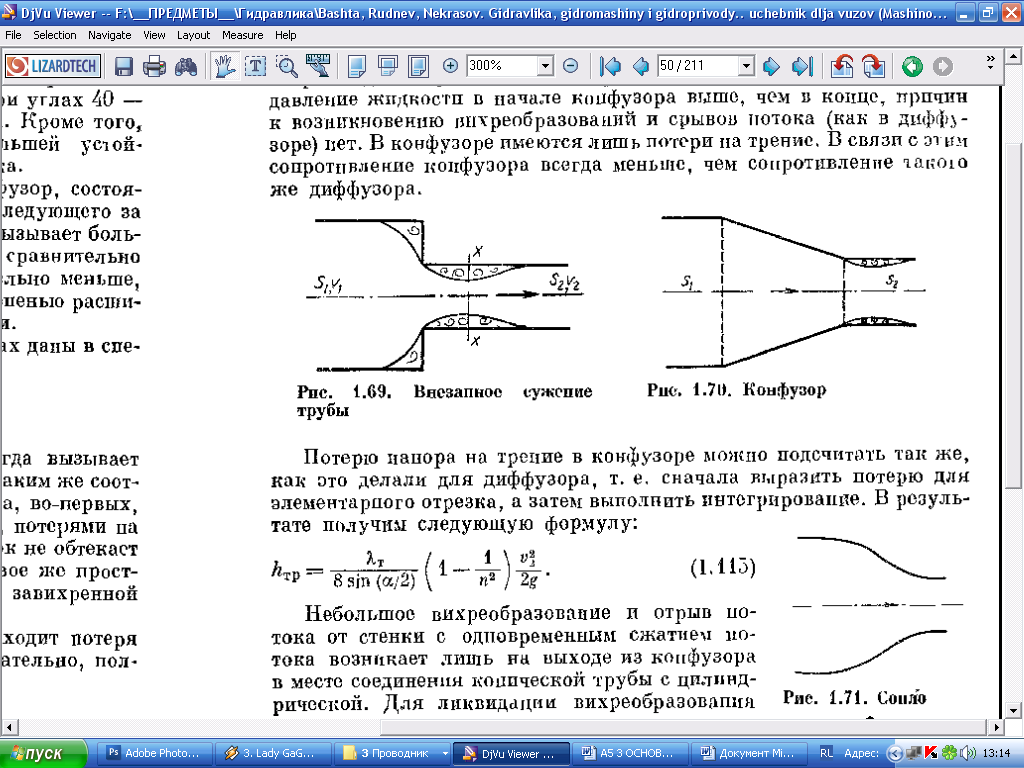
Рисунок 3.37

Течія рідини в конфузорі супроводжується зростанням швидкості і зменшенням тиску (₁  ₂, р₁  р₂), тому немає причин для виникання вихроутворення і зриву потоку. Тобто в конфузорі мають місто лише втрати на тертя. В зв’язку з цим втрати напору в конфузорі завжди менше втрат напору в дифузорі при однакових розмірах.

Втрату напору на тертя в конфузорі визначають так саме, як і для дифузора, за формулою

. (3.61)

Незначні втрати енергії від вихроутворення виникають на виході з конфузора на ділянці з’єднання конічної і циліндричної частин. Для усунення цього явища рекомендують конічну частину з’єднувати з циліндричною плавно.

Плавне звуження потоку називають соплом (рисунок 3.38).

Рисунок 3.38

Сопло дозволяє мати значний ступінь звуження при незначній довжині конфузора і невеликих втратах. Коефіцієнт опору сопла змінюється від 0,03 до 0,10 (_сопла = 0,03  0,1) і залежить від ступеня звуження і числа Re: більшим значенням числа Re відповідають менші величини _сопла і навпаки.

3.13.3.6 Поворот потоку

Поворот потоку може бути раптовим і поступовим (плавним). Раптовий поворот потоку обумовлює значні втрати енергії (рисунок 3.39).

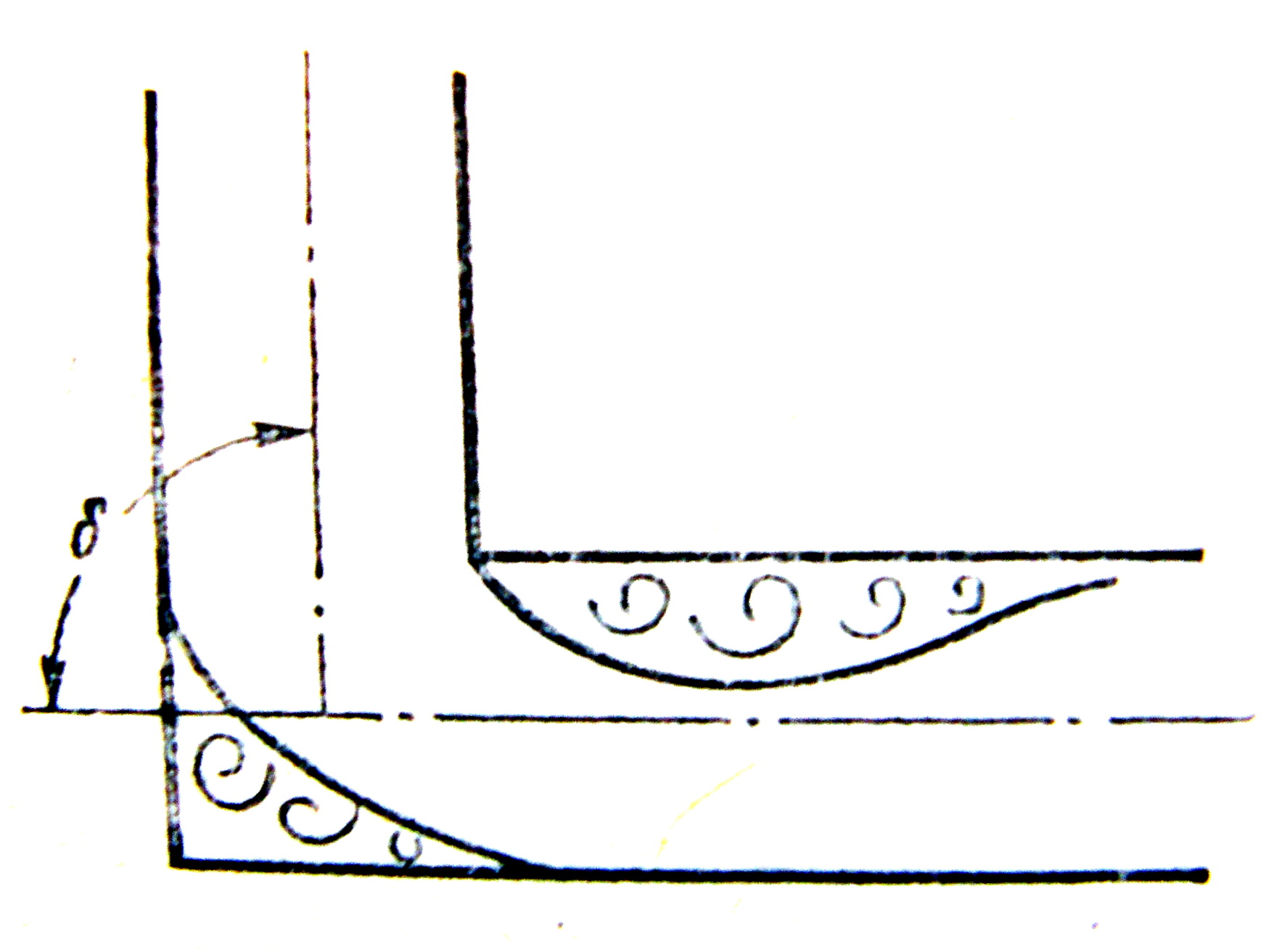
Рисунок 3.39

Причина втрат енергії – зони вихроутворення і тертя (внутрішнього і зовнішнього). Втрати енергії визначають за формулою

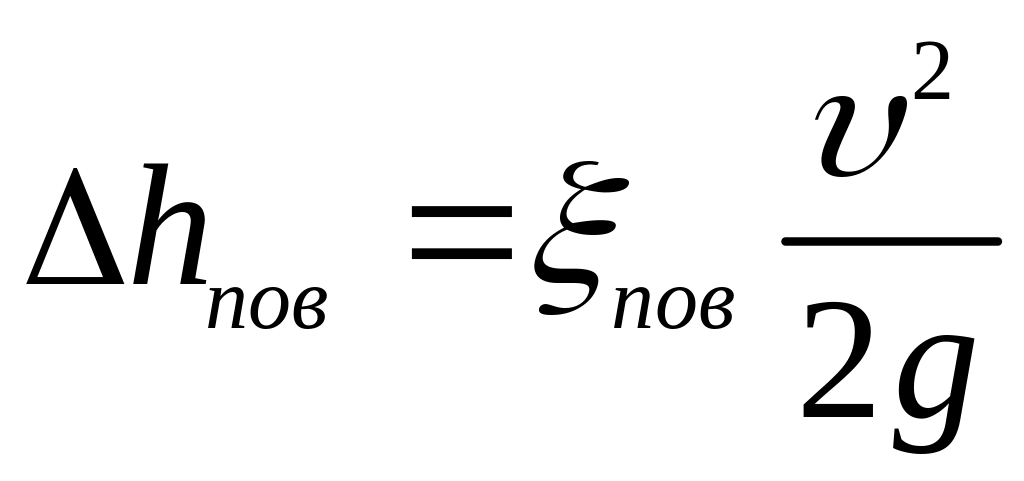, (3.62)

де _пов – коефіцієнт опору при повороті потоку.

Коефіцієнт опору _пов залежить від кута повороту потоку : чим більше кут , тим більше значення _пов.

Для круглого перерізу коефіцієнт опору _пов зростає зі збільшенням кута  до значення _пов = 1,0 при  = 90⁰ (рисунок 3.40).

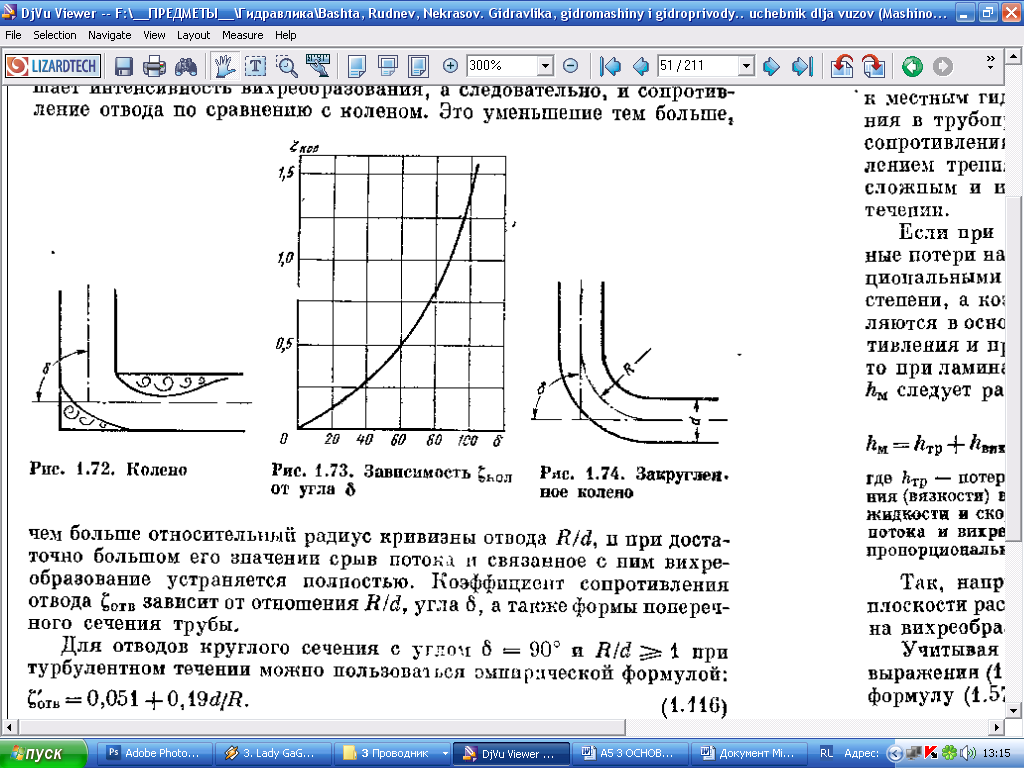
Рисунок 3.40

Поступовий поворот потоку називають відводом (рисунок 3.41).

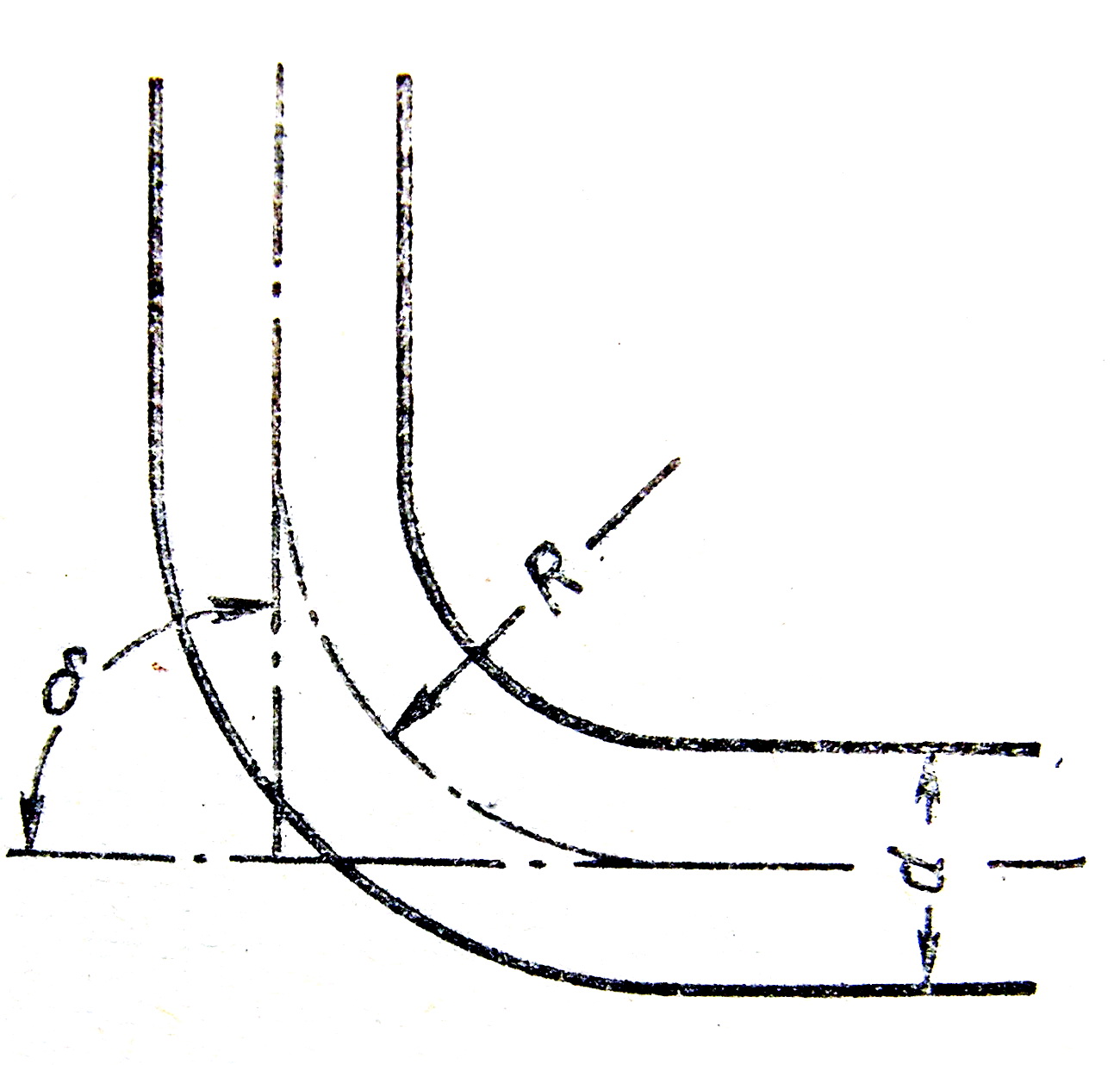
Рисунок 3.41

Поступовий (плавний) поворот потоку значно зменшує вихроутворення відносно раптового повороту, тому  . Величина коефіцієнту опору відводу залежить від співвідношення , величини кута  і форми перерізу каналу.

Для відводу круглого перерізу з кутом повороту  = 90 і  1 при турбулентному режимі можна користуватися емпіричною формулою

. (3.63)

Для кутів   70 коефіцієнт опору визначають за формулою

. (3.64)

Для кутів   100 коефіцієнт опору визначають за формулою

. (3.65)

Втрата напору, що визначається коефіцієнтом , враховує лише додатковий опір, який обумовлює поворот потоку. Тому для розрахунків трубопроводів, які мають відводи, довжину відводів необхідно включити в загальну довжину трубопроводу, для якої визначають втрати на тертя, і до цих втрат додати втрати відводу.

Слід зауважити, що у випадку ламінарного потоку теорема Борда-Карно не виконується; у випадку турбулентного потоку вона надійно виконується при числах Рейнольдса більше 3500 ( ).

Коефіцієнти місцевого опору при ламінарному потоці ми не розглядаємо, бо в інженерній практиці таки випадки майже не зустрічаються. В загальному випадку залежності будуть іншими.

Інколи величину втрат на місцевих опорах замінюють довжиною еквівалентної труби , на якій втрати по довжині дорівнюють очікуваним втратам на місцевих опорах. Тоді розрахункова довжина трубопроводу

. (3.66)

Числові значення наводяться в довідниках.