3.13.3.4 Поступове розширення потоку

Ділянка труби, яка поступово розширюється, називається дифузором (рисунок 3.33).

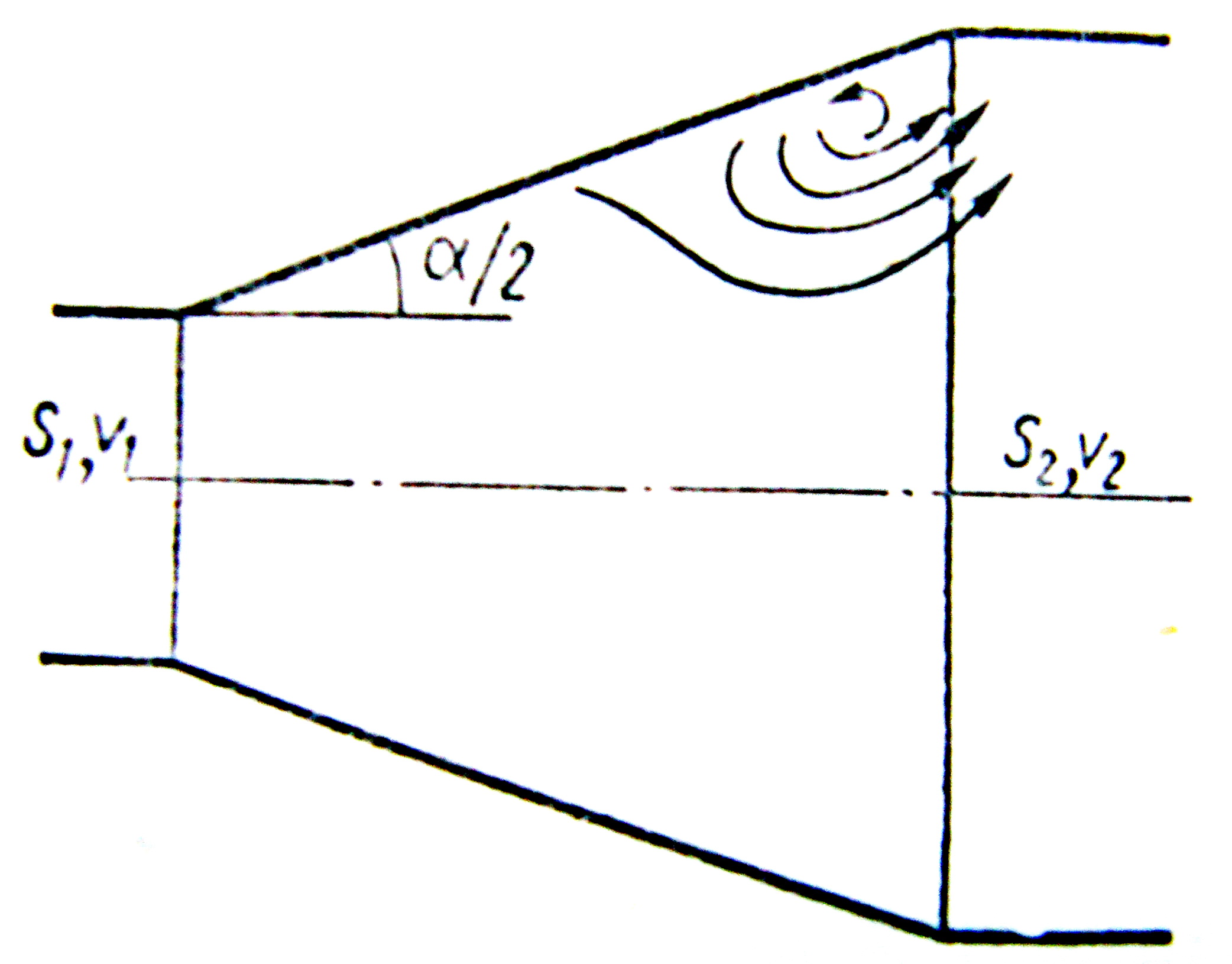
Рисунок 3.33

Для руху рідини в дифузорі характерно зменшення швидкості (  ) і збільшення тиску (  ). Частинки рухомої рідини долають збільшення тиску за рахунок кінетичної енергії, яка зменшується вздовж дифузора і в напрямку від осі до стінки дифузора. Шари рідини, які прилягають до стінок, мають таку малу кінетичну енергію, що зупиняються або починають рухатися в зворотному напрямку. Як наслідок, відбувається вихроутворення і відрив потоку від стінки дифузора. Інтенсивність цих явищ зростає зі збільшенням кута дифузора. Крім того, в дифузорі виникають втрати напору, які обумовлені тертям. Тому

, (3.54)

де – втрати напору, які обумовлені тертям;

– втрати напору, які обумовлені розширен-ням (вихроутворенням).

Спробуємо оцінити кожну із складових рівняння (3.54). Для визначення втрати напору на тертя розглянемо дифузор з діаметром входу і діаметром виходу , з прямолінійної твірної і кутом розширення  (рисунок 3.34).

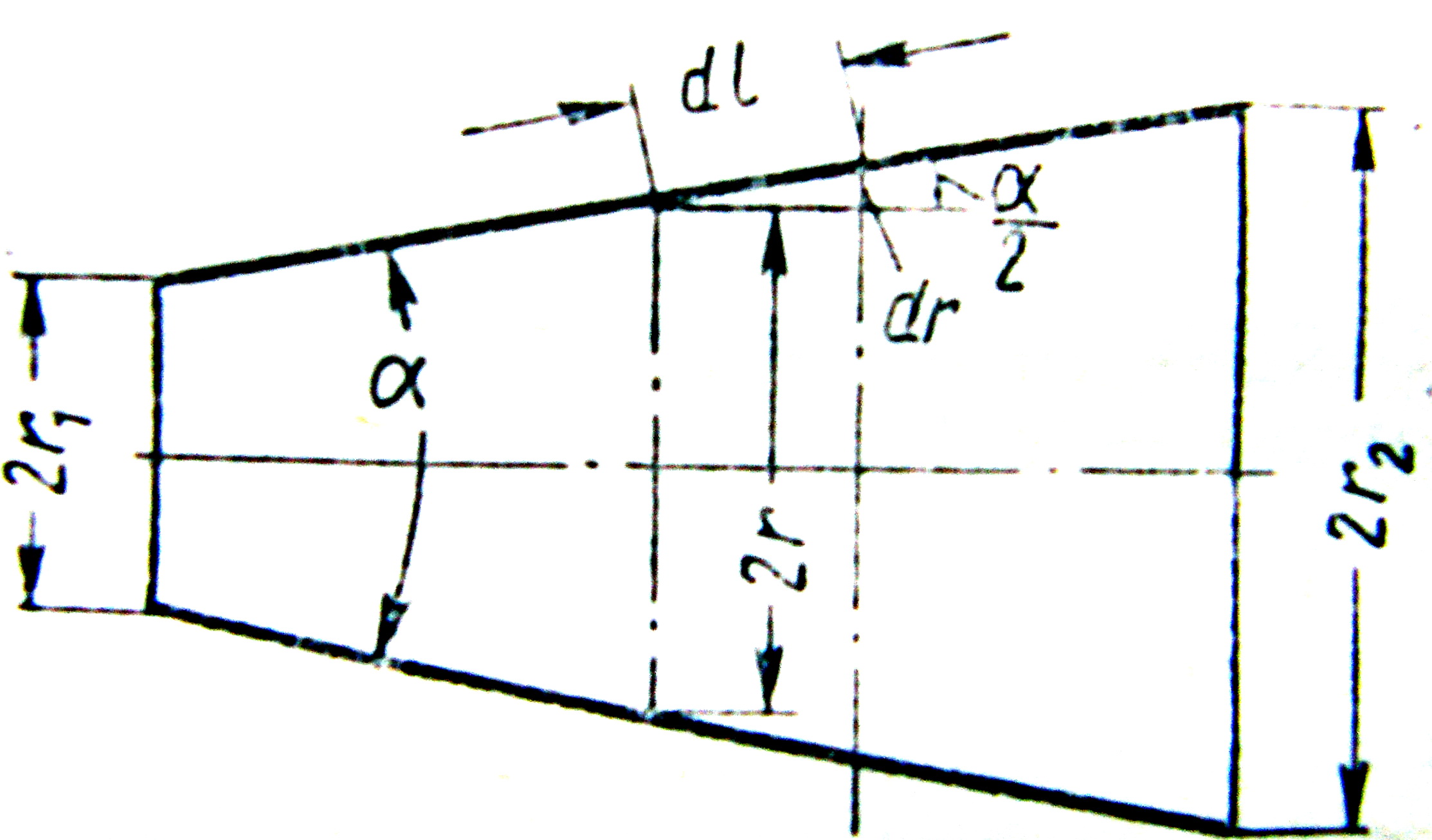
Рисунок 3.34

Радіус перерізу дифузора і швидкість руху рідини вздовж дифузора змінюються за величиною. Тому виділимо елементарний відрізок дифузора довжиною і діаметром , для нього знайдемо елементарну втрату напору на тертя за загальною формулою

,

де – середня швидкість в перерізі радіусом .

Величину знайдемо з елементарного трикутника

.

Величину  можна знайти з рівняння нерозривності

,

де ₁ - швидкість на вході в дифузор.

Тоді

.

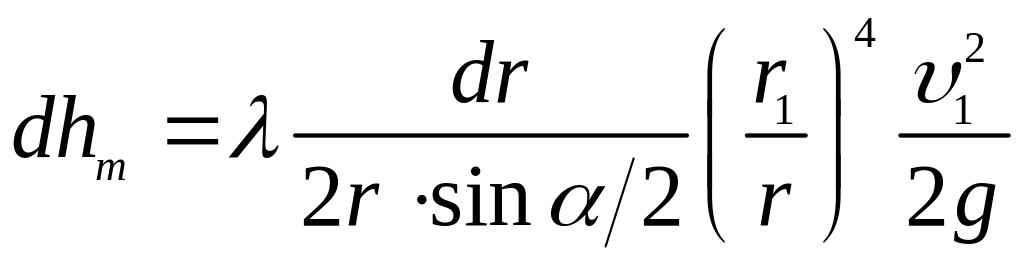Інтегруючи вздовж дифузора від до , дістаємо

.

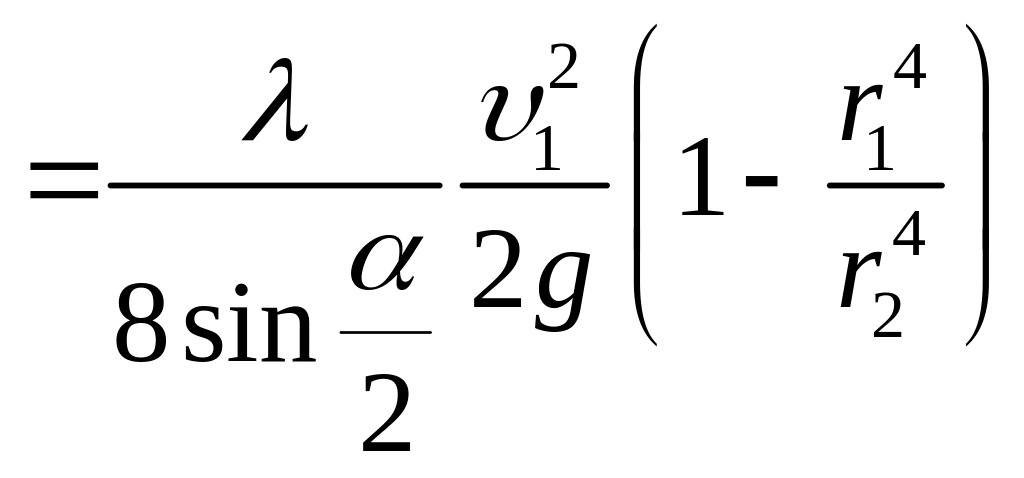Якщо ступінь розширення дифузора 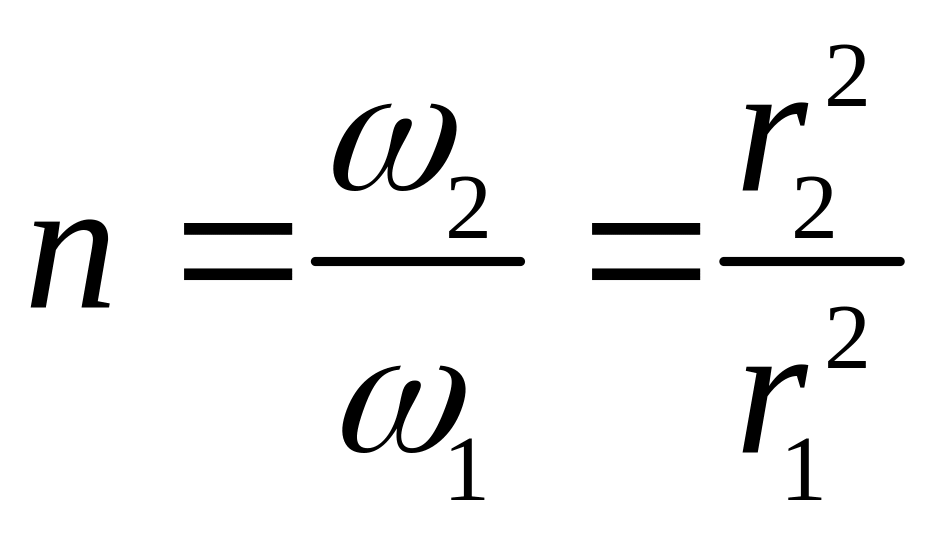, тоді

.

Остаточно втрати на тертя в дифузорі

. (3.55)

Друга складова повної втрати енергії в дифузорі (втрати на вихроутворення) має таку ж структуру, як і при раптовому розширенні, тільки менша за величиною. Тому для визначення використовують формулу (3.46), але з уточнюючим коефіцієнтом (   1):

.

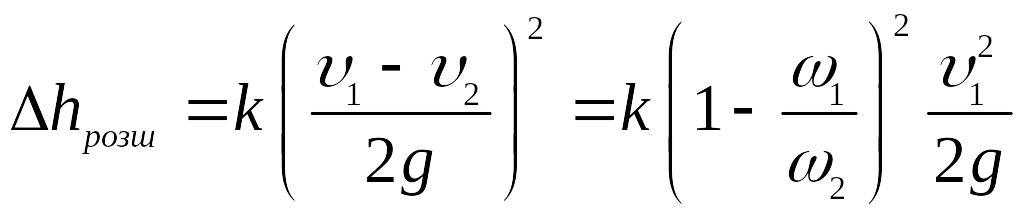Остаточно

. (3.56)

Для дифузорів з кутами розширення  від 5 до 20⁰ величину коефіцієнта можна визначати за формулою

. (3.57)

Загальна втрата напору в дифузорі

. (3.58)

Тому

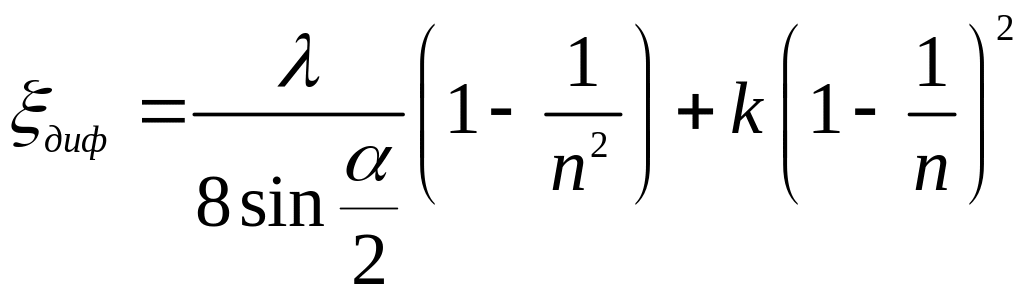. (3.59)

Тобто коефіцієнт опору дифузора залежить від кута розширення дифузора , коефіцієнта  і ступеня розширення дифузора : . При незмінних значеннях  і , якщо кут розширення дифузора збільшується, втрати напору на тертя зменшуються, але втрати від вихроутворення зростають. При зменшенні кута розширення дифузора навпаки: втрати зменшуються, але втрати зростають. Існує оптимальне значення кута , для якого коефіцієнт мінімальний. Графік залежності подано на рисунку 3.35.

Рисунок 3.35

Для виконується рівняння

.

Звідси

. (3.60)

Якщо величина змінюється в діапазоні від 0,015 до 0,025, а величина змінюється від 2 до 4, тоді оптимальний кут дифузора буде дорівнювати 6. Це відповідає експериментальним даним.

На практиці для зменшення довжини дифузора при заданому зазвичай приймають кут розширення дифузора  в діапазоні від 7 до 9. Це значення кута  є оптимальним для дифузорів з прямою віссю круглого і квадратного перерізів. Для прямокутних дифузорів із розширенням в одній площині оптимальний кут знаходиться в діапазоні від 10 до 12.

Якщо габарити не дозволяють приймати кут  оптимальним, доцільно перейти до спеціальних дифузорів (при  більше 15). До останніх відносяться ступінчасті і профільовані дифузори (рисунок 3.36).

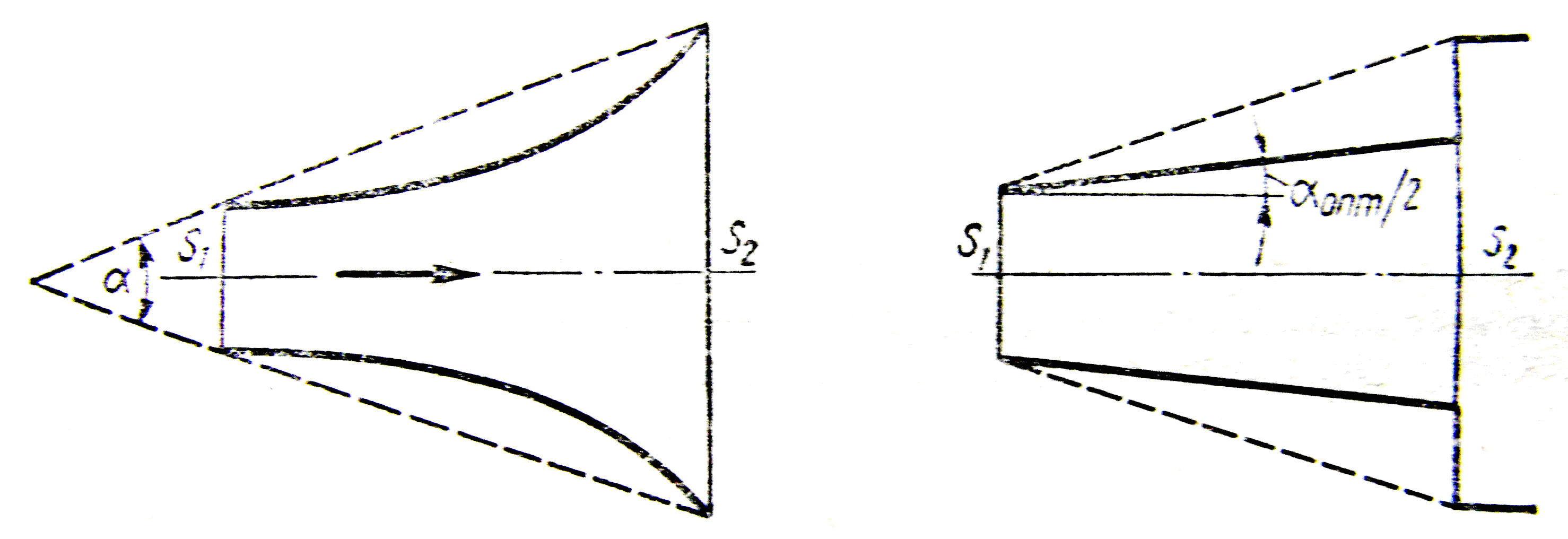
a б

Рисунок 3.36 – Спеціальні дифузори:

а – ступінчастий дифузор;

б – профільований дифузор

Ступінчастий дифузор складається із звичайного дифузора з оптимальним кутом розширення та раптового розширення. Профільований дифузор забезпечує постійний градієнт тиску вздовж осі дифузора .

Загальні втрати енергії спеціальних дифузорів значно менше, ніж звичайних той же довжини і ступеня розширення.