3.13.3.2 Раптове розширення потоку

У деяких випадках величини коефіцієнта можна визначити аналітично. Наприклад, французький інженер Борда запропонував залежність для вивчення втрати напору від раптового розширення потоку.

В випадку раптового розширення каналу потік зривається з кута і розширюється не раптово, як канал, а поступово. В просторі між потоками і стінкою каналу утворюються вихори, які зумовлюють втрату енергії. До того, між головними потоками і його вихровою частиною безперервно відбувається обмін частинками рідини.

Розглянемо потік рідини (рисунок 3.31), який із каналу з площиною витікає в канал з площиною (  ). Складемо залежність для визначення втрати енергії від раптового розширення потоку .

Для виведення залежності зробимо припущення:

а) розподіл швидкості у перерізах 1-1 і 2-2 рівномірний ( );

б) тертя на стінках каналу відсутнє;

в) розподіл тиску по площі перерізів і рівномірний.

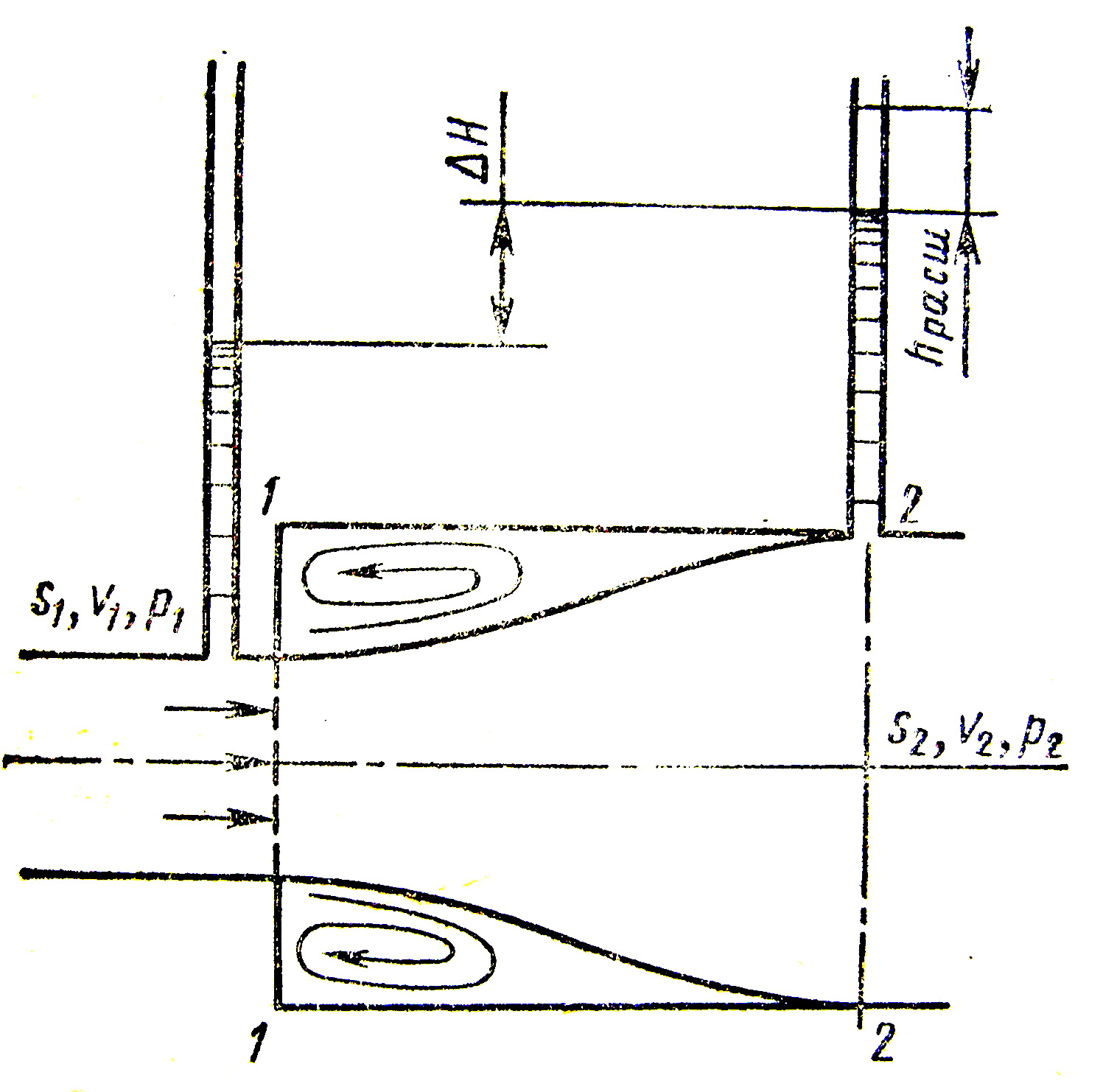
Рисунок 3.31

Складемо гідравлічне рівняння кінетичної енергії (рівняння Бернуллі) для перерізів 1-1 і 2-2:

,

або

. (3.44)

Враховуючи, що секундний імпульс зовнішніх сил дорівнює , відповідна зміна кількості руху

.

Тоді рівняння кількості руху

.

Поділимо ліву і праву частини рівняння на добуток  . Тоді

,

або

.

Перетворимо праву частину рівняння:

Тоді

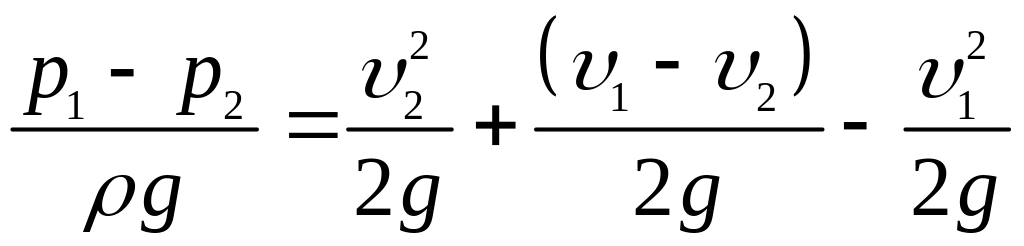. (3.45)

Якщо порівняти вирази (3.44) і (3.45), дістаємо рівняння

.

Тоді втрата енергії від раптового розширення потоку

. (3.46)

Тобто втрата напору (питомої енергії) при раптовому розширенні потоку дорівнює динамічному напору, якій підрахований по різниці швидкостей.

Втрати напору ще називають втратами Карно, а вираз (3.46) – теоремою Борда-Карно.

Визначимо, чому у цьому випадку дорівнює коефіцієнт раптового розширення . Згідно формулі Вейсбаха

.

Тоді, якщо виділити швидкісний напір із виразу (3.46), можна дістати :

,

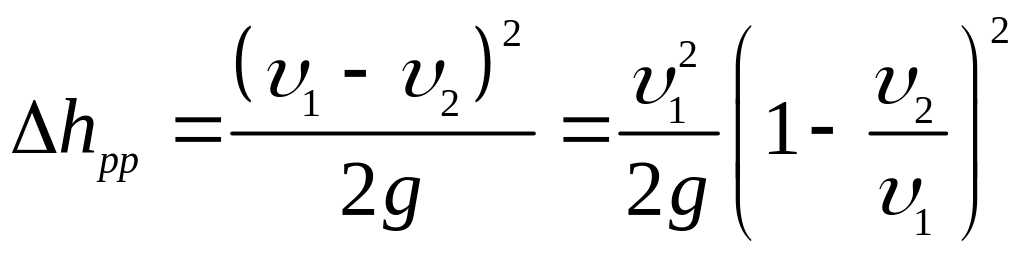або

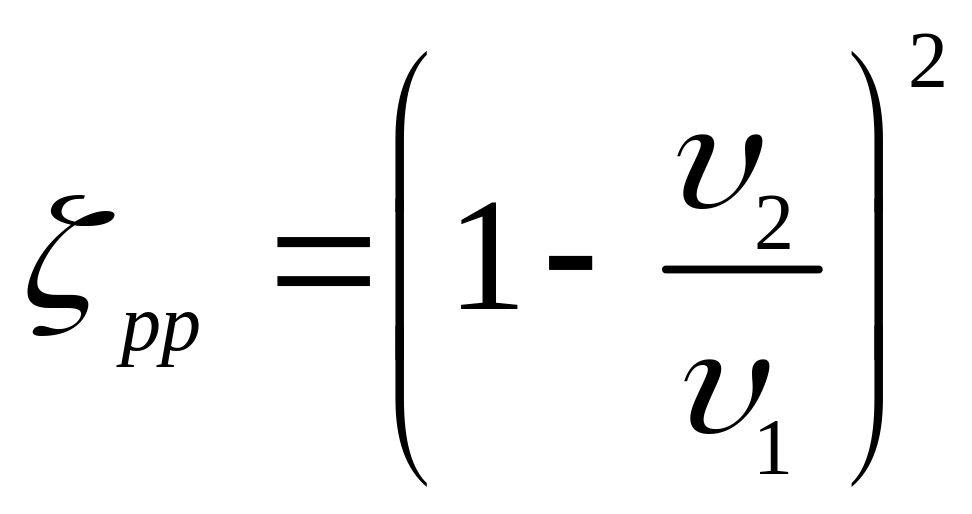. (3.47)

Якщо врахувати, що згідно рівняння нерозривності потоку , тоді

.

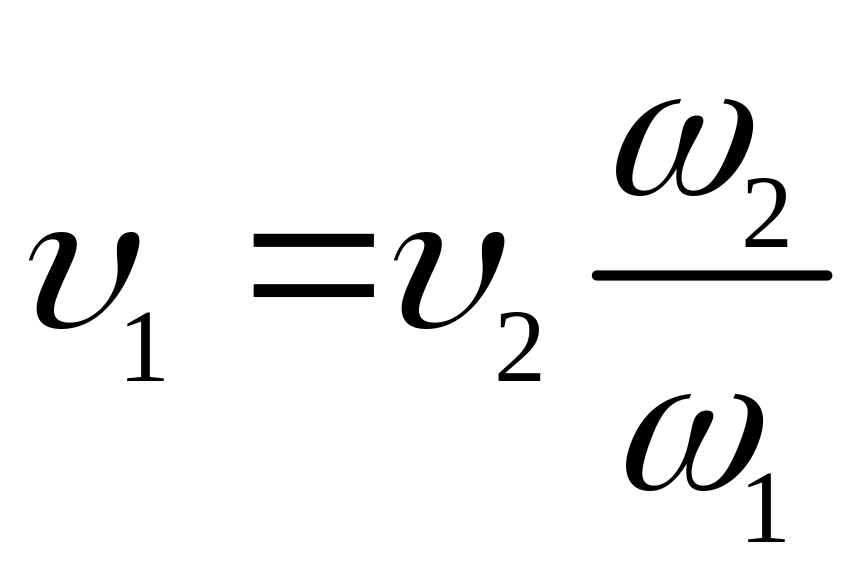Коефіцієнт раптового розширення

,

або

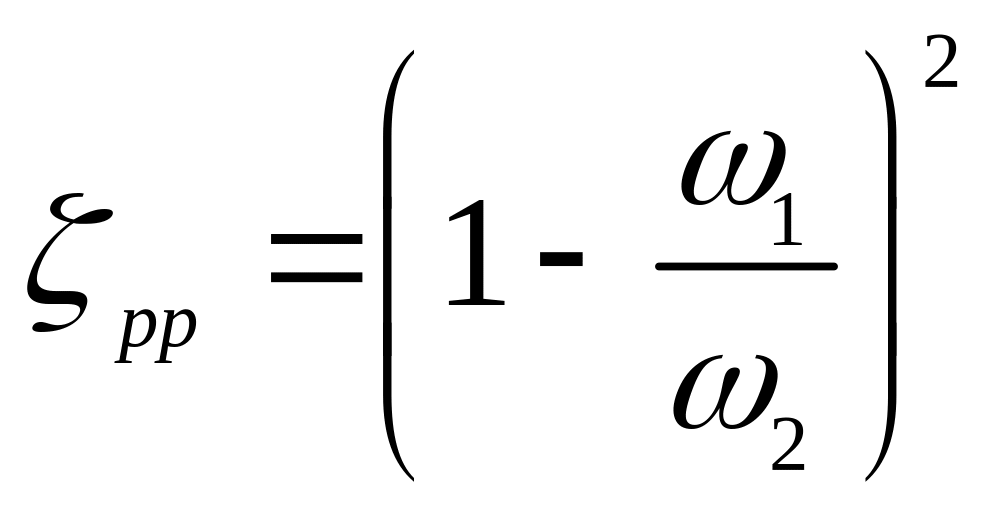. (3.48)

Для круглої труби , тому коефіцієнт раптового розширення в цьому випадку визначається за формулою

. (3.49)

Під час раптового розширення потоку до нескінченно великих розмірів (вихід в резервуар великих розмірів при , ) витрачається весь динамічний напір ( ). Коефіцієнт раптового розширення в цьому випадку

. (3.50)

3.13.3.3 Раптове звуження потоку

Раптове звуження потоку завжди обумовлює меншу втрату напору, ніж раптове розширення при однаковому співвідношенні площі перерізів 1-1 і 2-2 (рисунок 3.32).

Рисунок 3.32

В цьому випадку втрати енергії обумовлені, по-перше, тертям потоку при вході в вузьку трубку; по-друге, втратами на вихроутворення. Останні виникають за рахунок зриву з кута і звуження потоку (переріз x-x на рисунку 3.32), утворення простору з малорухомою рідиною. При подальшому розширенні потоку відбувається втрата енергії, яка визначається за теоремою Борда. Тому повна втрата енергії при раптовому звуженні потоку

, (3.51)

де – коефіцієнт опору, обумовлений тертям потоку при вході в вузьку трубу;

– швидкість потоку у самому вузькому перерізі;

– коефіцієнт раптового звуження.

Коефіцієнт раптового звуження залежить від співвідношення площі перерізів 1-1 і 2-2. На практиці для розрахунків використовують полуемпіричну формулу

, 3.52)

де – ступінь звуження: .

З виразу (3.52) витікає, що при (вхід в трубу із резервуару) коефіцієнт звуження

. (3.53)

Якщо надати вхідному куту округлої форми, можна значно зменшити втрату напору при вході в трубу.