3.13.2 Втрати напору по довжині
Втрати напору по довжині
– це втрати напору, які в чистому вигляді
виникають у прямих трубках і каналах
постійного перерізу. Цей вид втрат
енергії зумовлений виключно силами
тертя у рідині (внутрішніми і зовнішніми).
Загальна формула для розрахунку втрат по довжині
.
Проте значно зручніше
коефіцієнт втрат по довжині
пов’язувати із довжиною трубки.
Розглянемо ділянку трубопроводу довжиною і діаметром (рисунок 3.29).
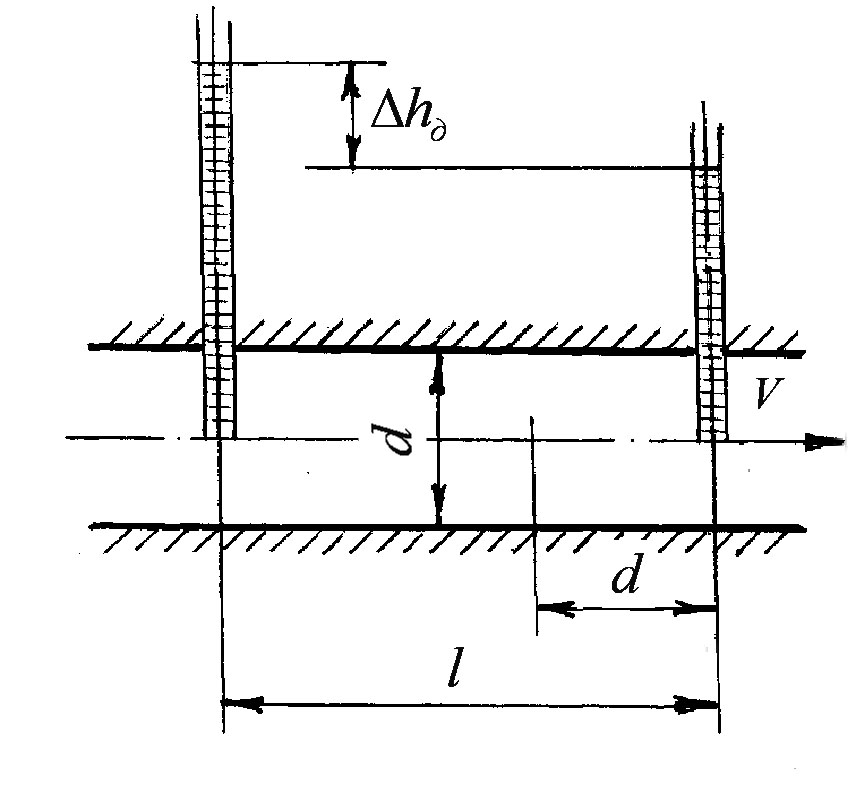
Рисунок 3.29
Позначимо коефіцієнт опору
відрізка труби довжиною
через
.
Тоді для відрізка труби довжиною
коефіцієнт опору буде в
раз більшим.
Тобто
.
Тоді
,
(3.42)
де
– втрати напору по довжині трубопроводу;
- гідравлічний коефіцієнт тертя, який визначають за дослідними даними;
- довжина трубопроводу;
– діаметр трубопроводу;
– швидкісний напір.
Формулу (3.42) запропонував французький вчений Дарсі в 1857 році на основі багатьох дослідів, проведених на паризькому трубопроводі. Тому вираз (3.42) називають формулою Дарсі.
3.13.3 Втрати напору на місцевих опорах
3.13.3.1 Види місцевих опорів
Втрати на місцевих опорах – це втрати, які обумовлені місцевими змінами конфігурації та розмірів потоку, що приводять до його деформації.
Місцеві опори розподіляють на раптове і поступове розширення, звуження та поворот потоку. Більш складні місцеві опори (засувка, дросель, діафрагма та ін.) можна уявити як комбінацію вищеназваних опорів.
Наприклад, якщо рідина тече через засувку, потік змінює свій напрямок, звужується, потім знов розширюється. При цьому відбувається інтенсивне вихроутворення.
На рисунку 3.30 проілюстровані деякі приклади місцевих опорів: раптове розширення або звуження потоку, поворот потоку, засувка, діафрагма, сопло, дросель.
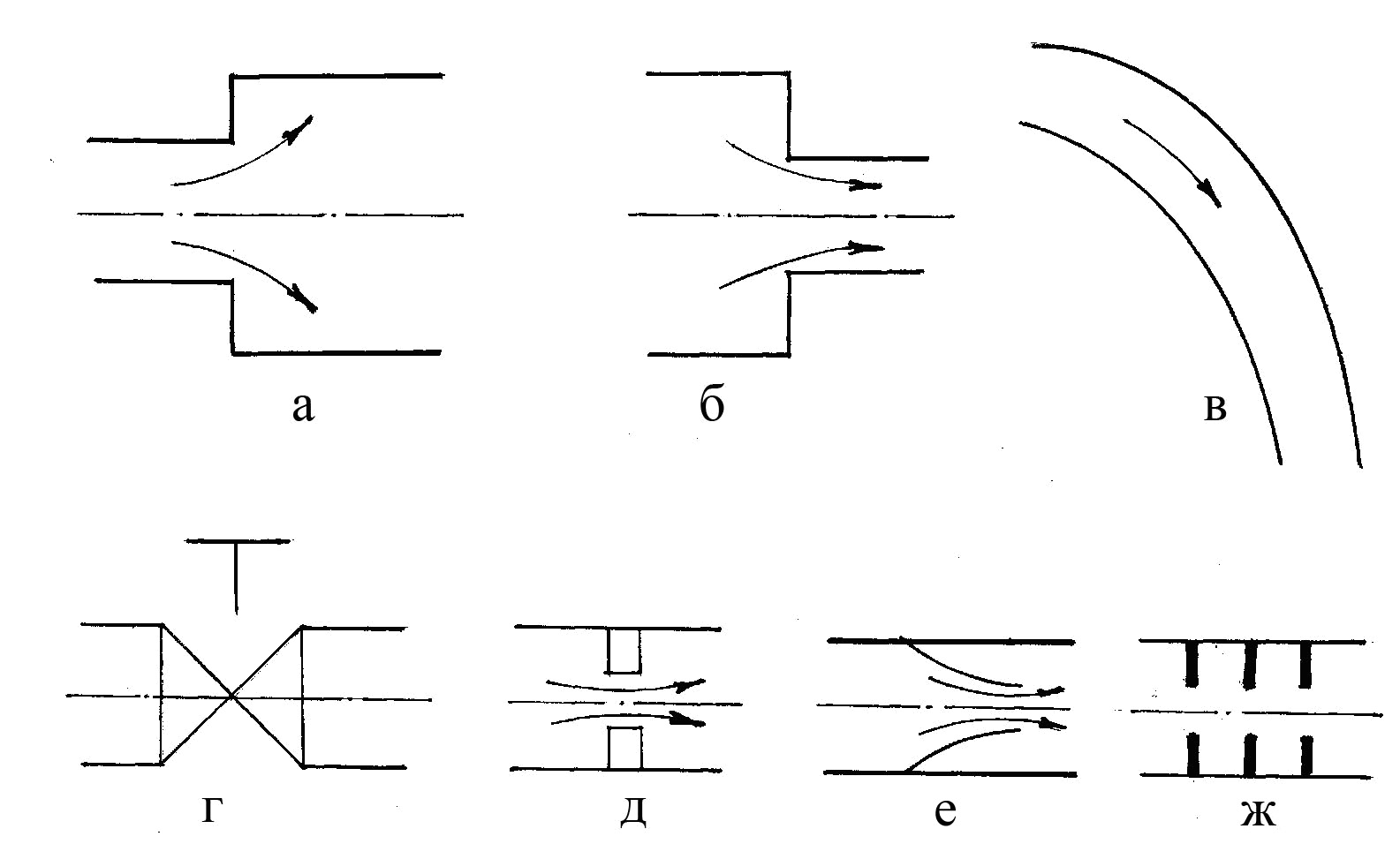
Рисунок 3.30 – Місцеві опори:
а – раптове розширення потоку;
б - раптове звуження потоку;
в – поворот потоку; г – засувка;
д – діафрагма; е – сопло; ж – дросель
Втрати енергії на місцевих опорах зручно визначити по загальній формулі, яку запропонував у 1840 р. Ю. Вейсбах:
,
(3.43)
де м – коефіцієнт місцевого опору, який визначають за даними експериментів.
Для кожного виду місцевого опору коефіцієнт м буде свій. Зазвичай величину м можна знайти в спеціальних довідниках (наприклад - Ідельчик «Довідник з гідравлічних опорів»).
Слід зауважити, що довжину
потоку, де відбувається втрата напору
на місцевому опорі, для розрахунків
вважають рівної нулю (
),
а величину місцевої втрати напору
відносять до конкретного перерізу
потоку.
На місцевих опорах внаслідок зміни розмірів і конфігурації потоку відбувається зміна швидкості та відрив транзитного потоку від стінки каналу і утворюються вихори. Тому втрата енергії на місцевих опорах відбувається не стільки за рахунок внутрішнього тертя, як за рахунок вихроутворення.