2.6 Закон розподілу тиску в газах
Закон розподілу тиску в газах залежить від висоти стовпа газу.
Так, при малій висоті стовпа газу можна прийняти густину незмінної за величиною ( ). Тоді
.
Після інтегрування маємо
. (2.21)
При великих висотах стовпа
(сотні і тисячі метрів) густина не є
сталою величиною (
)
і залежить від тиску
і температури
(
).
У випадку ізотермічної
атмосфери (
)
згідно закону Бойля-Маріотта
.
Тоді
.
Звідси
.
Тоді
.
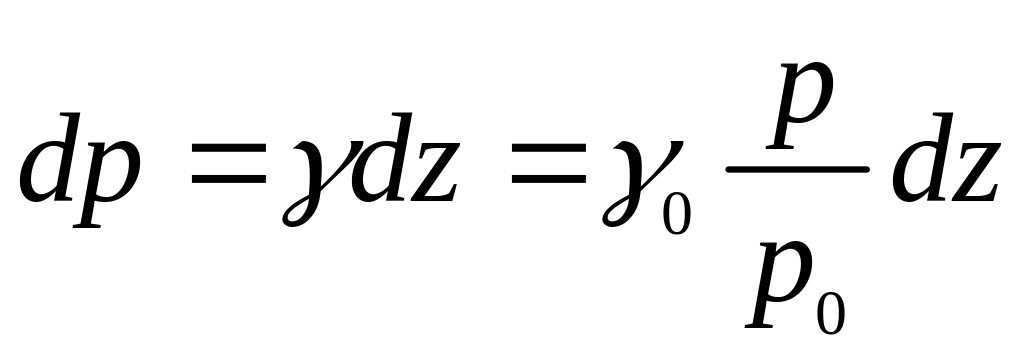Звідси
.
Після інтегрування маємо
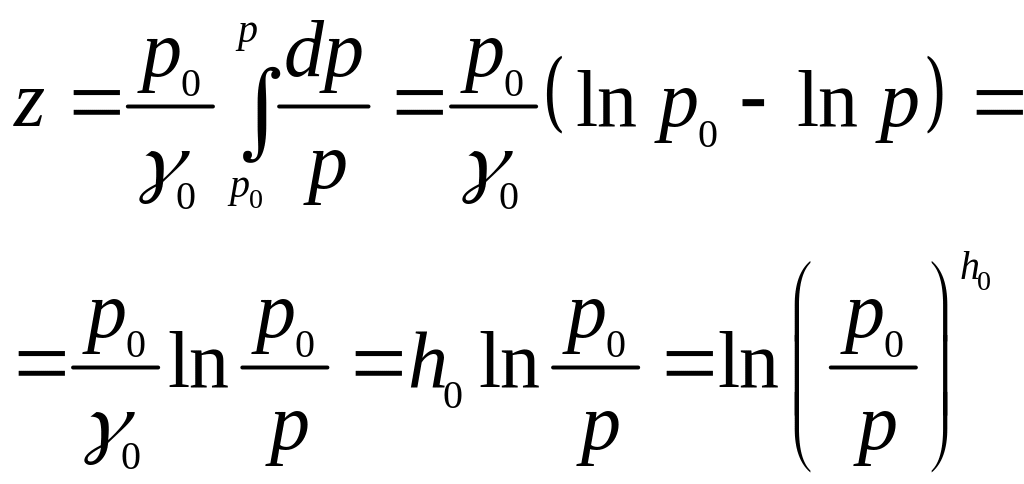(2.22)
Звідси
,
або
.
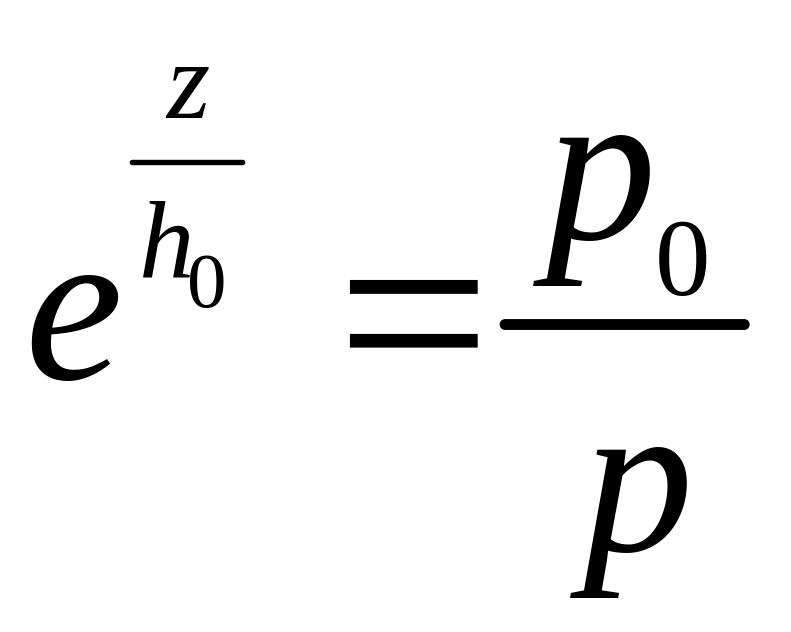Тоді
.
(2.23)
Раніше в (2.22) було здобуто
.
Тоді для двох різних висот і можна скласти рівняння
,
.
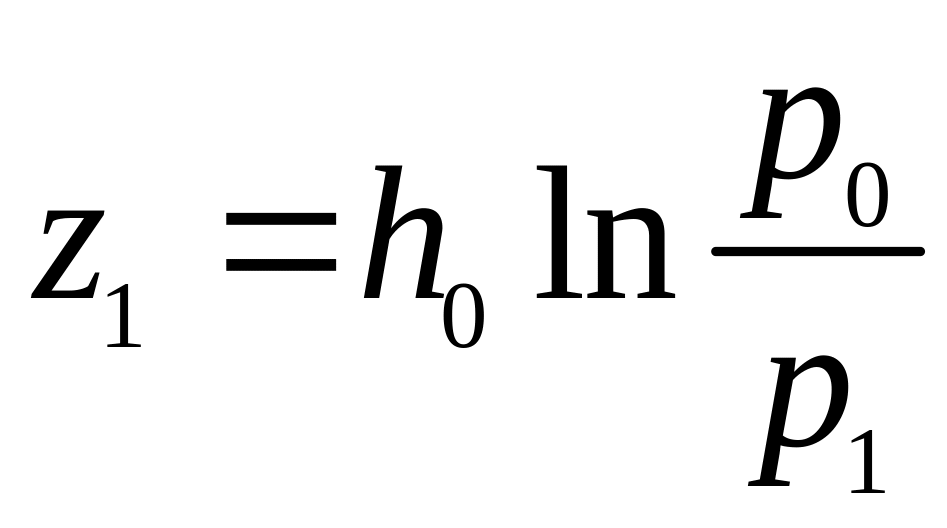Звідси дістаємо
.
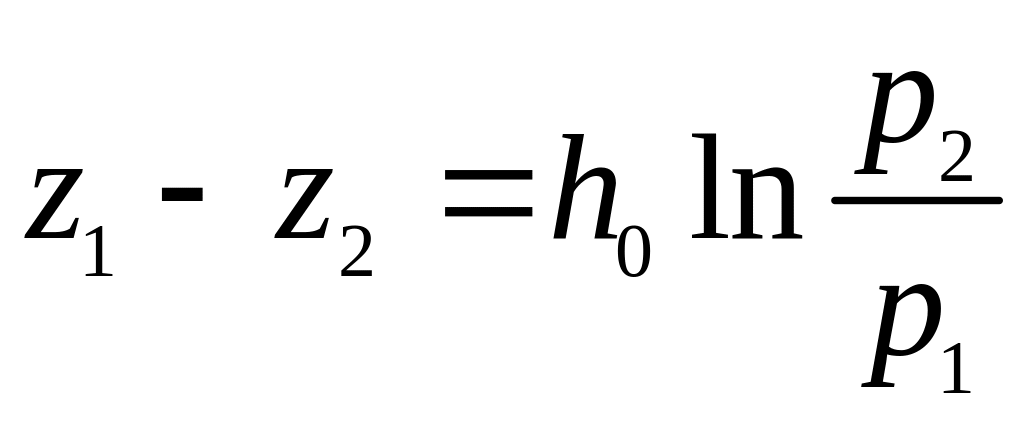(2.24)
Рівняння (2.24) називають барометричною формулою і використовують для визначення різниці висот по відомим тискам на цих висотах.
Позначимо різницю
через h,
тоді рівняння (2.24) можна записати
.
(2.25)
Тобто на малих висотах поблизу поверхні Землі тиск у газах розподіляється лінійно, на великих висотах (сотні і тисячі метрів від поверхні Землі) тиск у газах розподіляється еквіпотенціально (рисунок 2.10).
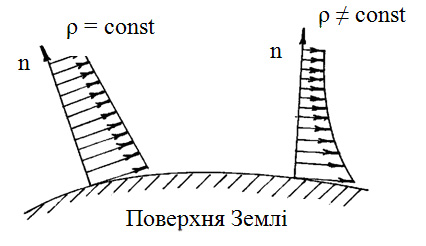
Рисунок 2.10
2.7 Відносний спокій рідини
Якщо на рідину, яка міститься в резервуарі, діють крім сил тяжіння ще і деякі інші масові сили, то такий стан рідини називають відносним спокоєм.
Розглянемо деякі приклади:
а) рідина міститься у цистерні
(бензобаку), яка рухається горизонтально
з прискоренням
(рисунок 2.11).
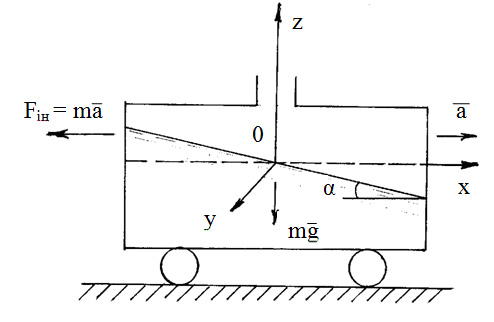
Рисунок 2.11
Треба врахувати, що на цистерну
діє сила
з прискоренням
(
),
а на рідину діє сила інерції
з прискоренням мінус
(
).
Тоді на рідину діють одиничні сили
,
,
.
Складемо диференціальне
рівняння рівноваги рідини в цистерні.
Відомо, що
,
на вільній поверхні рідини -
.
Тоді
.
(2.26)
Після інтегрування маємо
.
Для вільної поверхні
,
.
Тоді
.
Звідси
.
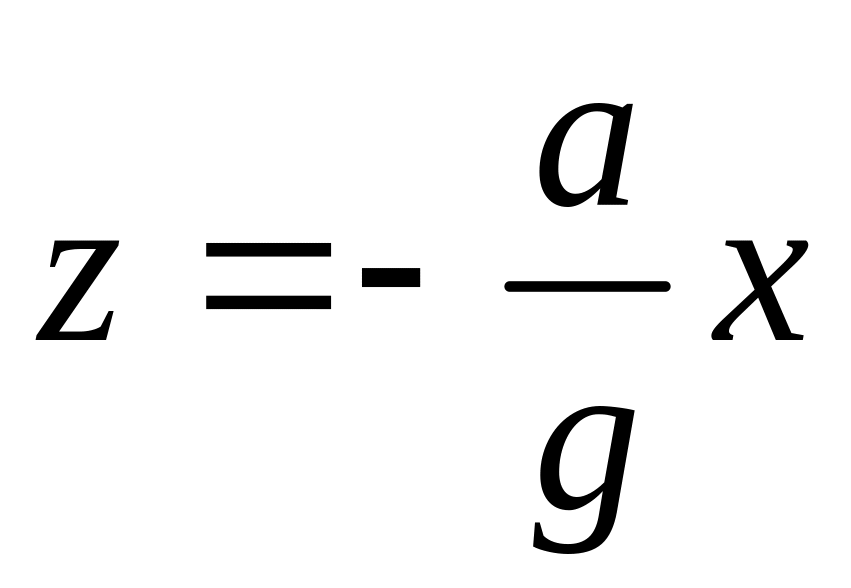(2.27)
Рівняння (2.27) показує, що
вільна поверхня рідини в цистерні є
площиною з кутом нахилу
.
Якщо
> 0,
то
< 0
і навпаки: якщо
< 0,
то
> 0.
Тобто при зменшенні швидкості руху
вільна поверхня рідини буде нахилена
в протилежний бік.
Розглянемо розподіл тиску в рідині у цистерні:
.
Після інтегрування маємо
.
(2.28)
Якщо
,
,
,
маємо
.
Звідси
.
(2.29)
Підставляючи (2.29) в (2.28), дістаємо
.
(2.30)
Рівняння поверхонь рівного тиску має вигляд:
;
(2.31)
б) резервуар з рідиною рухається з прискоренням у вертикальному напрямку.
В даному випадку на рідину
діють сила тяжіння
і сила інерції
.
Проекції на осі координат рівнодійної
сили будуть
,
,
(рисунок 2.12).
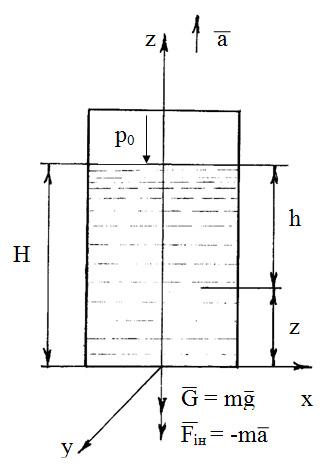
Рисунок 2.12
В даному випадку на рідину діють сила тяжіння і сила інерції . Проекції на осі координат рівнодійної сили - , , . Тоді диференціальне рівняння розподілу тиску в рідині набирає вигляду
.
Після інтегрування маємо
.
Якщо
,
,
тоді
.
Звідси
.
Тоді
.
Остаточно:
.
(2.32)
Якщо
,
можна записати:
.
(2.33)
Проаналізуємо вираз (2.33):
1) якщо
,
тоді
(
глибина занурення відносно вільної
поверхні);
2) якщо
< 0,
тоді
;
3) якщо
,
тоді
.
Це випадок, коли вага відсутня(невагомість).
Для поверхонь рівного тиску
.
Тобто
,
або
;
в) рідина міститься в циліндрі,
що обертається навколо вертикальної
осі з кутовою швидкістю 
(рисунок 2.13).
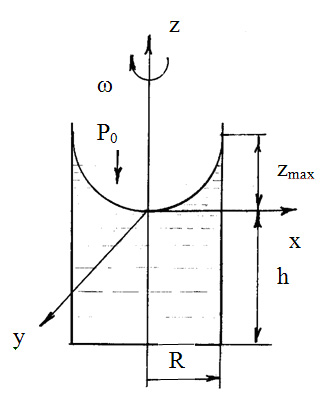
Рисунок 2.13
В даному випадку на рідину
діють відцентрова сила інерції та сила
тяжіння. Тому
,
,
.
Диференціальне рівняння рівноваги
рідини
.
Для даного випадку
,
або
.
Після інтегрування маємо
.
Якщо
,
,
тоді
.
У випадку
,
маємо
.
Тоді
.
Враховуючи, що
,
,
,
дістаємо
.
(2.34)
Рівняння вільної поверхні рідини в циліндрі як поверхні однакового тиску набирає вигляду
.
Після інтегрування маємо
,
або
.
(2.35)
Тобто у цьому випадку поверхня однакового тиску є параболоїд обертання.
На вільній поверхні
,
тоді
,
або
.
(2.36)
Максимальне підвищення рідини
в циліндрі буде при
,
тоді
.
(2.37)
В цьому випадку тиск на стінки циліндра
.
(2.38)
Якщо вісь обертання
горизонтальна, на рідину будуть діяти
сили
,
,
.
Тоді тиск на стінки циліндра
,
(2.39)
або
.
(2.40)
При значних швидкостях обертання циліндра тиск на його стінки дуже великий. Це використовують в фрікційних муфтах, де для з’єднання необхідно забезпечити значні сили нормального тиску, та в технологічному процесі відцентрового лиття.