8.6. Методы изучения связи качественных признаков

При наличии соотношения между вариацией качественных признаков говорят об их ассоциации, взаимосвязанности. Для оценки связи в этом случае используют ряд пока­зателей.

Коэффициент ассоциации и контингенции. Для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп, применяются коэффициенты ассоциации и контингенции.

Для их вычисления строится таблица, которая показывает связь между двумя явле­ниями, каждое из которых должно быть альтернативным, то есть состоящим из двух каче­ственно отличных друг от друга значений признака (например, изделие годное или брако­ванное).

Таблица 8.8.

Таблица для вычисления коэффициентов ассоциации и контингенции

a	b	a+b
c	d	c+d
a+c	b+d	a+b+c+d

Коэффициенты вычисляются по формулам:

ассоциации:

(8.14.)

контингенции:

(8.15.)

Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь счи­тается подтвержденной, если К_а ≥ 0,5 или К_к ≥ 0,3 .

Пример. Исследуем связь между участием населения одного из городов в экологи­ческих акциях и уровнем его образования. Результаты обследования характеризуются следующими данными:

Таблица 8.9.

Зависимость участия населения города в экологических акциях от образовательного уровня

Группы рабочих	Численность населения города	Из них
		Участвующих в акциях	не участвующих в акциях
Имеют среднее образование Не имеют среднее образование	100 100	78 32	22 68
Итого	200	110	90

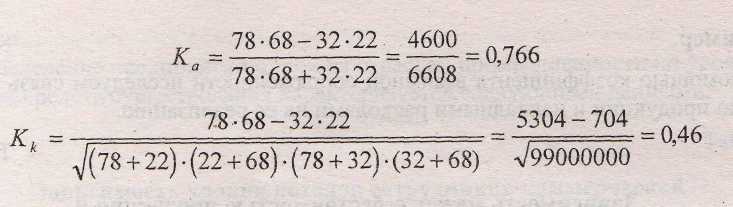
Таким образом, связь между участием населения города в экологических акциях и его образовательным уровнем имеет место, но не столь существенна.

Когда каждый из качественных признаков состоит более чем из двух групп, то для определения тесноты связи возможно применение коэффициентов взаимной сопряжен­ности Пирсона и Чупрова. Эти коэффициенты вычисляются по следующим формулам:

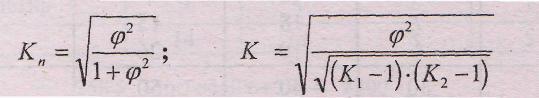(8.16.)

Где φ² - показатель взаимной сопряженности;

φ - определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот соответствующего столбца и строки. Вычитая из этой суммы «1», получим величину φ²:

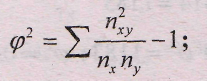
K₁ - число значений (групп) первого признака; К₂ - число значений (групп) второго признака.

Чем ближе величина К_п и К_ч к 1 тем теснее связь.

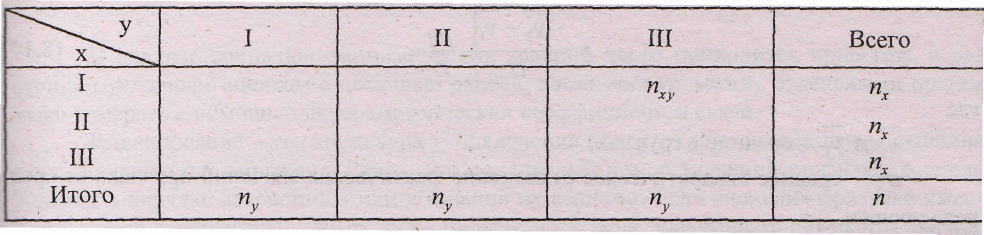
Таблица 8.10.

Вспомогательная таблица для расчета коэффициента

взаимной сопряженности

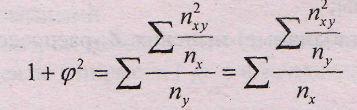
Пример.

С помощью коэффициента взаимной сопряженности исследуем связь между себестоимостью продукции и накладными расходами на ее реализацию.

Таблица 8.11.

Зависимость между себестоимостью продукции и

накладными расходами на ее реализацию

Накладная расходы	Себестоимость			Итого
	Низкая	Средняя	Высокая
Низкие Средние Высокие	19 7 4	12 18 10	9 15 26	40 40 40
Итого	30	40	50	120

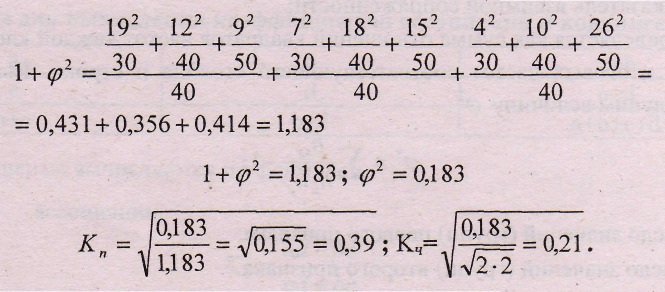
Связь слабая.

Особое значение для оценки связи имеет биссериальный коэффициент корреляции, который дает возможность оценить связь между качественным альтернативным и количественным варьирующим признаками. Данный коэффициент вычисляется по формуле:

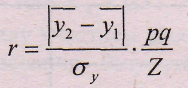(8.17)

где

у¯₂ и у¯_х - средние в группах;

σ_y - среднее квадратическое отклонение фактических значений признака от средyнего уровня;

р - доля первой группы;

q - доля второй группы;

Z - табулированные (табличные) значения Z -распределения в зависимости от р.

Пример.

Распределение предприятий одной из отраслей промышленности по уровню дохода и источникам средств существования характеризуется следующими данными:

Таблица 8.12.