1.4. Застосування теореми Гауса

Поле безупинне розподілених зарядів

Визначимо тепер за допомогою теореми Остроградського - Гауса напруженість полючи для ряду випадків.

1. Електричне поле рівномірне зарядженої сферичної поверхні.

Сфера радіусом R. Нехай заряд +q рівномірно розподілений по сферичній поверхні радіуса R. Розподіл заряду по поверхні характеризується поверхневою щільністю заряду (мал.4).

Поверхневою щільністю заряду називають відношення заряду до площі поверхні, по якій він розподілений. . . у СІ .

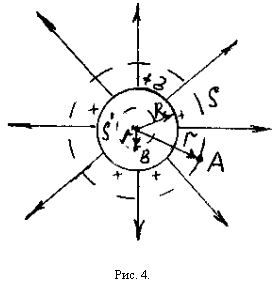
Визначимо напруженість полючи:

а) поза сферичною поверхнею,

б) усередині сферичної поверхні.

а) Візьмемо крапку А, що відстоїть від центра зарядженої сферичної поверхні на відстані r>R. Проведемо через неї думкою сферичну поверхню S радіуса r, що має загальний центр із зарядженою сферичною поверхнею. З розуміння симетрії очевидно, що силові лінії є радіальними прямими перпендикулярними до поверхні S і рівномірно пронизують цю поверхню, тобто напруженість по всіх крапках цієї поверхні постійна по величині. Застосуємо теорему Остроградського - Гауса до цієї сферичної поверхні S радіуса r. Тому повний потік через сферу дорівнює N = E 4π ²S; N=E . З іншої сторони . Дорівнюємо: . Звідси: при r>R.

У такий спосіб: напруженість, створювана рівномірно зарядженою сферичною поверхнею, поза її така ж, як якби весь заряд знаходився в її центрі (мал.5).

б) Знайдемо напруженість полючи в крапках, що лежать усередині зарядженої сферичної поверхні. Візьмемо крапку У віддалену від центра сфери на відстані r´ <R, і проведемо через цю крапку сферичну поверхню має загальний центр із зарядженою сферичною поверхнею.

З розуміння симетрії ясно, що напруженість повинна бути чисельно однакова на всій обраній поверхні сфери S і нормальна до неї. Застосовуючи теорему Остроградського - Гауса до сферичної поверхні S на підставі формули: N=E S, S=4p тому що заряд усередині сфери S q = 0, те . Тоді , E = 0 при r<R. Отже, напруженість електричного полючи у всіх крапках усередині рівномірно зарядженої сферичної поверхні дорівнює нулю.

2. Напруженість полючи рівномірно зарядженої нескінченної площини

Розглянемо електричне поле створюване нескінченною площиною , зарядженої з щільністю , постійної у всіх крапках площини. По розуміннях симетрії можна вважати, що лінії напруженості перпендикулярні до площини і спрямовані від її в обидва боки (мал.6).

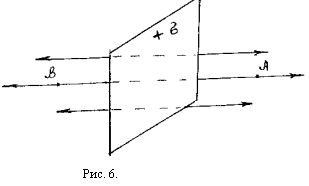
Виберемо крапку А, що лежить праворуч від площини й обчислимо в цій крапці, застосовуючи теорему Остроградського - Гауса. Як замкнуту поверхню виберемо циліндричну поверхню таким чином, щоб бічна поверхня циліндра була рівнобіжна силовим лініям, а його підстави і рівнобіжні площини і підстава проходить через крапку А (мал. 7). Розрахуємо потік напруженості через розглянуту циліндричну поверхню. Потік через бічну поверхню дорівнює 0, тому що лінії напруженості рівнобіжні бічної поверхні. Тоді повний потік складається з потоків і минаючих через підстави циліндра і . Обоє ці потоку позитивні = + ; = ; = ; = = ; N = 2 .

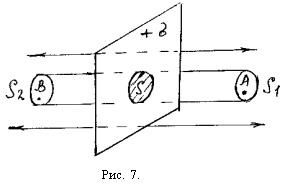
S - ділянка площини лежачий усередині обраної циліндричної поверхні. Заряд усередині цієї поверхні дорівнює q.

. тоді ;

СГСЭ ;

Отже величина не залежить від положення розглянутої крапки А и визначається тільки поверхневою площиною зарядів . Вектор σ усюди спрямований перпендикулярно площини,

а) якщо σ >0 від площини (мал. 8).

б) якщо σ <0 тоді до площини (мал. 9).

3. Поле двох рівнобіжних площин

Площини заряджені різнойменними зарядами з плотностями +s і -s (мал.10). напруженість полів обох площин між площинами спрямовані в одну сторону, отже, їхня геометрична сума є їхньою арифметичною сумою у вакуумі .

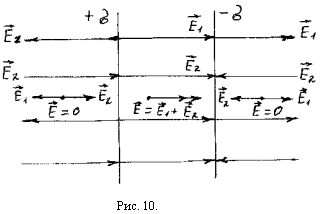
І так: у всіх крапках простору між площинами, вектор напруженості має однакову величину і спрямований від позитивно зарядженої площини до негативно зарядженої площини, тобто поле між площинами однорідне. Поза цими площинами поле дорівнює "0" .

Потенційну енергію взаємодії двох крапкових зарядів q1 і q2, що знаходяться у вакуумі на відстані r12 друг від друга можна обчислити по:

(1)

Розглянемо систему, що складається з N крапкових зарядів: q1, q2,..., qn.

Енергія взаємодії такої системи дорівнює сумі енергій взаємодії зарядів узятих попарно:

. (2)

У формулі 2 підсумовування виробляється по індексах і і k (і№k). Обидва індекси пробігають, незалежно друг від друга, значення від 0 до N. Доданки, для яких значення індексу і збігається зі значенням індексу k не враховуються. Коефіцієнт 1/2 поставлений тому, що при підсумовуванні потенційна енергія кожної пари зарядів враховується двічі. Формулу (2) можна представити у виді:

, (3)

де jі - потенціал у крапці перебування і-го заряду, створюваний всіма іншими зарядами:

.

Енергія взаємодії системи крапкових зарядів, що обчислюється по формулі (3), може бути як позитивної, так і негативної. Наприклад вона негативна для двох крапкових зарядів протилежного знака.

Формула (3) визначає не повну електростатичну енергію системи крапкових зарядів, а тільки їхню взаємну потенційну енергію. Кожен заряд qі, узятий окремо має електричну енергію. Вона називається власною енергією заряду і являє собою енергію взаємного відштовхування нескінченно малих частин, на які його можна думкою розбити. Ця енергія не враховується у формулі (3). Враховується тільки робота затрачувана на зближення зарядів qі, але не на їхнє утворення.

Повна електростатична енергія системи крапкових зарядів враховує також роботу, на утворення зарядів qіиз нескінченно малих порцій електрики, стерпних з нескінченності. Повна електростатична енергія системи зарядів завжди позитивна. Це легко показати на прикладі зарядженого провідника. Розглядаючи заряджений провідник як систему крапкових зарядів і з огляду на однакове значення потенціалу в будь-якій крапці провідника, з формули (3) одержимо:

. (4)

1.5. Приклад рішення задачі на обчислення електричних полів

Металеве кільце радіусом R має заряд q. Чому рівні напруженість полючи і потенціал:

а) на відстані а від центра уздовж осі, перпендикулярної площини кільця;

б) у центрі кільця?

Рішення:

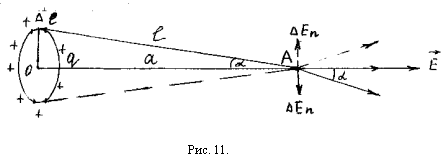
Візьмемо елемент кільця , що створює в крапці А електричне поле напруженістю (мал.11). Вектор напруженості спрямований по лінії , що з'єднує елементи кільця з зарядом ( - можна прийняти за крапковий заряд) із крапкою А. Для перебування сумарного полючи треба геометрично скласти всі полючи, створювані кожним елементом: . Вектор напруженості має дві складові: (нормальна і дотична складові).

Складові від кожних двох діаметрально розташованих елементів взаємно знищуються, тоді результуюче поле і вектор спрямований уздовж осі. З малюнка 24 випливає, що ; де . З огляду на, що напруженість полючи крапкового заряду одержимо: .

Для перебування потенціалу φ підсумовуємо алгебраїчно потенціали, створювані окремими елементами :

У центрі кільця а = 0, тому з попереднього випливає, що ;

Л.С.Жданов. Підручник по фізиці для середніх спеціальних навчальних закладів. § 16.1-16.6, стор.151 - 157.

§ 17.1-17.4, стор.162 - 167 § 17.13 - 17.16, стор. 184 -189. § 17.17 стор. 190.

Питання для самоперевірки.

1.Сформулюйте закон збереження заряду.

2.З якою метою уводиться вектор електричної індукції, його сутність?

3.Висновок теореми Остроградського - Гауса.

4.Какое електричне поле є рівномірне зарядженої сферичної поверхні?

5.Як визначити поверхневу щільність заряду рівномірно зарядженої нескінченної площини ?

6. Як визначити напруженість полю ?

1.6. Рішення задач по електростатиці

1) Зробіть схематичний чи малюнок креслення, на якому укажіть усі сили, що діють на даний заряд.

2) Якщо даний заряд знаходиться в поле декількох крапкових зарядів, потрібно скористатися принципом незалежності дії полів.

3) У випадку, коли заряд чи спочиває рухається чи рівномірно прискорено , прийоми рішення задач такі ж як у механіку.

4) Якщо при взаємодії заряджених тіл між ними відбувається перерозподіл зарядів, до складених рівнянь додають рівняння закону збереження заряду.

5) Коли встановлений тип з'єднання конденсаторів і ясно, як знайти їхню загальну ємність, подальший розрахунок зведеться до того, щоб визначити зв'язок між зарядами і напругами на конденсаторах і виразити через них ємності конденсаторів.

6) При рішенні задач електростатики і відповідях на якісні питання корисно мати на увазі наступне.

1. Позитивні електричні заряди, надані самим собі, рухаються в електричному полі від крапок з великим потенціалом до крапок з меншим потенціалом. Негативні заряди переміщаються в зворотному напрямку.

2. Напруженість полючи усередині статично зарядженого провідника дорівнює нулю.

3. Потенціал Землі і всіх тіл, з'єднаних провідником із Землею, приймається рівним нулю.

4. Робота сил електростатичного полючи по будь-якому замкнутому контурі дорівнює нулю.

Приклади рішення задач

Задача №1.

Дві кульки, розташовані на відстані 10см друг від друга, мають однакові негативні заряди і взаємодіють із силою 0,23мН. Знайдіть число "надлишкових" електронів на кожній кульці.

Дане: Рішення:

r = 10 см 0,1 м Електричний заряд дискретний, тобто q = Ze,

F = 0,23 мН 2,3·10^-4 Н де е = 1,6·10^-19 Кл - заряд електрона, а Z -

число електронів. Кульки можна вважати

Z = ? крапковими тілами, тому силу взаємодії між ними у вакуумі визначимо за законом Кулона: F = kq²/r².

Зробивши підстановку, одержимо:

F = k(Ze)²/r²,

відкіля випливає:

Z = r/e √F/k.

Зробимо обчислення:

Z = 0,1/1,6·10^-19 2,3·10^-4/9·109 = 1·10¹¹. Відповідь: 1·10¹¹.

Задача №2.

Земля - електрична заряджене космічне тіло. Заряд Землі негативний. Знаючи, що напруженість електростатичного полючи Землі на її поверхні дорівнює 130 Н/Кл і приймаючи радіус Землі рівним 6,4·10⁶ м, визначите електричний заряд Землі і поверхневу щільність заряду.

Дане: Рішення:

Е = 130 Н/Кл Напруженість полючи, створюваного зарядженим

R = 6,4·10⁶ м тілом сферичної форми, визначається так само, як

для крапкового заряду. При цьому вважається, що весь

q = ? заряд тіла зосереджений у центрі цього тіла:

σ = ? Е = kq/R², відкіля q = ER²/k. Поверхнева щільність заряду по визначенню дорівнює:

σ = q/S, де

S - площа сферичної поверхні, рівна

S = 4πR².

Зробимо обчислення:

q = 130·40,96·10¹¹ \9·10⁹ = 5.9·10⁹(Кл)

σ = 5.9·10⁵\ 4π(6.4 ·10⁶)²= 1.1·10^-9(Кл\м²)

Відповідь: 5.9·10⁹(Кл), 1.1·10^-9(Кл\м²)

Задача №3.

Діелектриком у конденсаторі служить пропарафинирований папір товщиною 0,15мм, пробивна напруга якої 15 кВ/мм. Яке максимально допустиме напруження можна подати на конденсатор, якщо запас міцності дорівнює 2,25?

Дане: Рішення:

d₁ = 0,15 мм 1,5·10^-4 м Запас міцності визначається

Uпр/d = 15 кВ/мм 1,5·10⁷ В/м відношенням граничного

k = 2,25 напруги, при якому відбувається

пробій діелектрика до припустимого,

Uдоп = ? при який можлива нормальна робота конденсатора, тобто

k = Uпр/Uдоп.

Для даного конденсатора пробивна напруга дорівнює:

Uпр = (Uпр/d)d1. Отже,

Uдоп =(Uпр/d)d1\к.

Зробимо обчислення:

Uдоп = 1.5·10⁷·1.5·10^-4\2.25=1000(В)

Відповідь: 1000(В)

Задача №4.

На відстані 3м друг від друга розташовані два крапкових негативних заряди q₁ = - 9 нКл і q₂ = - 36 нКл. Коли в деякій крапці помістили заряд q₀, те всі три заряди виявилися в рівновазі. Знайдіть відстань між зарядами q₁ і q₂ .

Дане: Рішення:

r = 3 м

q₁ = - 9 нКл - 9·10^-9 Кл

q₂ = - 36 нКл - 36·10^-9 Кл

r₀₁ = ?

Усі заряди знаходяться в спокої. Отже, заряд q0 повинний бути позитивним і знаходитися між даними зарядами на одній прямій. Як відомо, тіло знаходиться в спокої, якщо дія усіх сил скомпенсовано.

Умова рівноваги заряду q0 буде наступним:

F₀₁+ F₀₂ = 0

F₀₁ - сила притягання, що діє на заряд q0 з боку заряду q1,

F₀₂ - сила притягання, що діє на заряд q0 з боку заряду q2.

У скалярній формі рівняння буде наступним:

F₀₁ – F₀₂ = 0 чи F₀₁ = F₀₂.

Сили F₀₁ і F₀₂ визначимо за законом Кулона, використовуючи принцип суперпозиції, по якому кожну силу можна визначити незалежно від дії інших сил.

F₀₁ = kq₀q₁\r₀₁² і F₀₂ =kq₀q₂\(r – r₀₁₎²

Дорівнявши ці сили, одержимо:

kq₀q₁\r₀₁² = kq₀q₂\(r – r₀₁₎²

Проведемо скорочення і перетворимо це рівняння відносно r₀₁:

(q₂ – q₁)r₀₁² + 2rq ₁r₀₁ – q ₁r² = 0.

Для простоти рішення обчислимо попередньо коефіцієнти при r01 в отриманому квадратному рівнянні і після наступного скорочення одержимо рівняння:

r₀₁² + 2r₀₁ - 3 = 0.

Відкинемо негативне значення кореня, тому що якщо заряд q0 буде розташований ліворуч від заряду q1, рівноваги зарядів не буде.

Отже, r₀₁ = 1м.

Відповідь: r₀₁ = 1м.

Задача №5.

При розрядці батареї, що складає з 20 паралельно включених однакових конденсаторів, виділилося 10 Дж тепла. Ємність кожного конденсатора 4 мкф. Визначите, до якої різниці потенціалів були заряджені конденсатори.

Дане: Рішення:

n = 20 При рівнобіжному з'єднанні n - го кількості

Q = 10 Дж однакових конденсаторів загальна ємність дорівнює:

С₁ = 4 мкф 4·10^-6 ф С = n₁ . Кількість теплоти, що буде

віддано в навколишнє середовище при розрядці батареї,

U = ? дорівнює енергії електричного полючи

Q = З U²/2 = n ₁U²/2, відкіля

U = √2Q/NС₁.

Зробимо обчислення:

U = √2·10/20 4·10^-6 = 500(В).

Відповідь: 500(В).

Задача №6.

Визначите поверхневу щільність заряду на пластинах плоского конденсатора, якщо відомо, що електрон, не мав початковій швидкості, пройшовши шлях від однієї пластини до іншої, здобуває швидкість 109м/с. Відстань між пластинами 3 см.

Дане: Рішення:

Vo = 0

V = 1·10⁹ см/с 1·10⁷ м/с

d = 3 см 0,03 м

е = 1,6·10^-19 Кл

σ= ?

По визначенню σ = q/S, де S - площа пластини конденсатора.

Заряд на обкладці конденсатора дорівнює q = СU, а ємність конденсатора: С = εε ₀S/d.

Напруга між обкладками конденсатора визначимо, знаючи роботу, що робить електричне поле для того, щоб повідомити електрону кінетичну енергію. За законом збереження енергії маємо:

mv²/2 = eU, де

m = 9,1·10^-31 кг - маса електрона,

е = 1,6·10^-19 Кл - заряд електрона.

Зробивши підстановку, одержимо:

σ = ε ₀mv²/2de.

Зробимо обчислення:

σ = 8,85·10^-12·9,1·10 ^-311·10¹⁴/2·0,03·1,6·10^-19 = 8,4·10^-8 (Кл/м²)

Відповідь: 8,4·10^-8 (Кл/м²)

Задача №7.

Визначите кількість електричної енергії, що перейшла в тепло при з'єднанні конденсаторів ємністю 2 мкФ і 0,5 мкФ, заряджених до напруги

100 В и 50 В відповідно, однойменно зарядженими пластинами.

Дане: Рішення:

С₁ = 2 мкФ 2·10^-6 Ф При з'єднанні конденсаторів у батарею

С₂ = 0,5 мкФ 5·10^-6 Ф змінюється їхня загальна ємність, а значить і

енергія.

U₁ = 100 В За законом збереження енергії маємо:

U₂ = 50 В Q = E₁ – E₂, де Е₁ - енергія конденсаторів до

з'єднання, Е₂ - енергія конденсаторів після їх

Q = ? з'єднання в батарею.

Е₁ = С ₁U ₁²/2 + С ₂ U ₂²/2 і Е₂ = (С₁ + С₂) U²/2.

При рівнобіжному з'єднанні конденсаторів заряд батареї дорівнює сумі зарядів на обкладках конденсаторів, тому загальна напруга U буде дорівнює:

U = (q₁ + q₂) / (C₁ + C₂), де

q ₁ = C ₁U ₁ - заряд на пластинах першого конденсатора,

q ₂ = C ₂U ₂ - заряд на пластинах другого конденсатора.

Зробивши підстановку і деякі перетворення, одержимо:

Q = (C ₁U ₁² + C ₂U₂²) /2 - (C ₁U ₁ + C ₂U₂)²/2 (C₁ + C₂).

Усі величини виражені в одній системі одиниць, формула у відношенні розмірності має простий вид, тому при обчисленні використовуємо тільки числові значення величин:

Q = (2·10^-6·1·10⁴ + 0.25·10^-6·2.5·10³ )\2 - (2·10^-6 ·100 + 0.5·10^-6·50)\2(2·10^-6+0.5· 10^-6) =5·10^-4(Дж)

Відповідь: 5·10^-4(Дж)